 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【高校物理】閉管:のように、長さ15cmの閉管に3倍振動の定常波ができている。音速を3.4✕10^2m/sとし、開口端補正は無視できるものとして、次の各問に答えよ。(1) 気柱に生じている定常波の波…

単元:
#物理#熱・波・音#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
図のように、長さ15cmの閉管に3倍振動の定常波ができている。音速を3.4✕10^2m/sとし、開口端補正は無視できるものとして、次の各問に答えよ。
(1) 気柱に生じている定常波の波長はいくらか。
(2) 気柱から出ている音の振動数はいくらか。
この動画を見る
図のように、長さ15cmの閉管に3倍振動の定常波ができている。音速を3.4✕10^2m/sとし、開口端補正は無視できるものとして、次の各問に答えよ。
(1) 気柱に生じている定常波の波長はいくらか。
(2) 気柱から出ている音の振動数はいくらか。
【受験算数】 東西にのびる線路がある。ある時A君が線路の近くに立っていると、西から特急、東から急行が近づいてきて、A君のちょうど目の前ですれちがい始めた。すれちがい始めてから15秒後に線路の向こう側…

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
東西にのびる線路がある。ある時A君が線路の近くに立っていると、西から特急、東から急行が近づいてきて、A君のちょうど目の前ですれちがい始めた。すれちがい始めてから15秒後に線路の向こう側が見えた。特急と急行の列車の長さがそれぞれ240m、270mで、速さの比が4:3である。
(1)特急と急行の速さはそれぞれ秒速何mか。
(2)A君の真東にいたB君も同じ特急と急行を見ていた。B君の目の前を急行が通過し始めてから、特急が通過し終わるまでの18と3/4秒間はずっと線路の向こう側は見えないままだった。A君とB君の間の距離は何mか。
この動画を見る
東西にのびる線路がある。ある時A君が線路の近くに立っていると、西から特急、東から急行が近づいてきて、A君のちょうど目の前ですれちがい始めた。すれちがい始めてから15秒後に線路の向こう側が見えた。特急と急行の列車の長さがそれぞれ240m、270mで、速さの比が4:3である。
(1)特急と急行の速さはそれぞれ秒速何mか。
(2)A君の真東にいたB君も同じ特急と急行を見ていた。B君の目の前を急行が通過し始めてから、特急が通過し終わるまでの18と3/4秒間はずっと線路の向こう側は見えないままだった。A君とB君の間の距離は何mか。
【英語】私立一貫校向け英語教材Lesson6-2 Stage3の英文解説

単元:
#英語(高校生)#英文法#関係代名詞・関係副詞・複合関係詞
教材:
#NT ENGLISH SERIES#中高教材#Third Edition Stage3#Lesson6
指導講師:
理数個別チャンネル
問題文全文(内容文):
I can't believe what you said.
What we should think about seriously is climate change.
This book is what I have been looking for.
You should listen to what the experts say.
Tell us what you need for your research.
この動画を見る
I can't believe what you said.
What we should think about seriously is climate change.
This book is what I have been looking for.
You should listen to what the experts say.
Tell us what you need for your research.
【受験算数】 川下のA地点から川上のB地点まで3km。Aを出た船が毎分20mの速さでBに向かって進むと、30分後に、川下から上ってきたモーターボートに追いこされた。それから20分後に、ふたたび…

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
川下のA地点から川上のB地点まで3km。Aを出た船が毎分20mの速さでBに向かって進むと、30分後に、川下から上ってきたモーターボートに追いこされた。それから20分後に、ふたたびモーターボートが下ってくるのに出会った。モーターボートは、Bで休まないで引き返し、川を上る速さと下る速さの比は4:5。モーターボートの静水時の速さと川の流れの速さを求めよ。
この動画を見る
川下のA地点から川上のB地点まで3km。Aを出た船が毎分20mの速さでBに向かって進むと、30分後に、川下から上ってきたモーターボートに追いこされた。それから20分後に、ふたたびモーターボートが下ってくるのに出会った。モーターボートは、Bで休まないで引き返し、川を上る速さと下る速さの比は4:5。モーターボートの静水時の速さと川の流れの速さを求めよ。
【数C】【空間ベクトル】3点A(3,6,0)、B(1,4,0)、C(0,5,4)の定める平面ABCに、点P(3,4,5)から垂線PHを下ろす。線分PHの長さを求めよ。

単元:
#空間ベクトル#空間ベクトル#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#空間ベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
3点A(3,6,0)、B(1,4,0)、C(0,5,4)の定める平面ABCに、点P(3,4,5)から垂線PHを下ろす。線分PHの長さを求めよ。
この動画を見る
3点A(3,6,0)、B(1,4,0)、C(0,5,4)の定める平面ABCに、点P(3,4,5)から垂線PHを下ろす。線分PHの長さを求めよ。
【受験算数】 川下のA地点から川上のB地点まで3.4km。Aを出た船が毎分80mの速さでBに向かって進むと、5分後に、川下から上ってきたモーターボートに追いこされた。それから15分後に、ふたたび…

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
川下のA地点から川上のB地点まで3.4km。Aを出た船が毎分80mの速さでBに向かって進むと、5分後に、川下から上ってきたモーターボートに追いこされた。それから15分後に、ふたたびモーターボートが下ってくるのに出会った。モーターボートは、Bで休まないで引き返し、川を上る速さと下る速さの比は5:6。モーターボートの静水時の速さと川の流れの速さを求めよ。
この動画を見る
川下のA地点から川上のB地点まで3.4km。Aを出た船が毎分80mの速さでBに向かって進むと、5分後に、川下から上ってきたモーターボートに追いこされた。それから15分後に、ふたたびモーターボートが下ってくるのに出会った。モーターボートは、Bで休まないで引き返し、川を上る速さと下る速さの比は5:6。モーターボートの静水時の速さと川の流れの速さを求めよ。
【受験算数】 S駅には100段のエスカレーターとその横に同じ段数の階段がある。太郎君がこのエスカレーターを歩いてのぼると60段のぼって上の階に着いた。また次郎君がこのエスカレーターを歩いてのぼると…

単元:
#算数(中学受験)#速さ#速さその他
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
S駅には100段のエスカレーターと、その横に同じ段数の階段がある。太郎君がこのエスカレーターを歩いてのぼると、60段のぼって上の階に着いた。また、次郎君がこのエスカレーターを歩いてのぼると、上の階に着くまでの時間が太郎君より25%多くかかった。
(1)太郎君と次郎君が階段を歩いてのぼるときの速さの比を求めよ。
(2)太郎君は歩いて階段をのぼり始めた。次郎君は太郎君よりおくれてエスカレーターを歩いてのぼり始めると、同時に上の階に着いた。次郎君は太郎君が何段のぼったときにのぼり始めたか。
この動画を見る
S駅には100段のエスカレーターと、その横に同じ段数の階段がある。太郎君がこのエスカレーターを歩いてのぼると、60段のぼって上の階に着いた。また、次郎君がこのエスカレーターを歩いてのぼると、上の階に着くまでの時間が太郎君より25%多くかかった。
(1)太郎君と次郎君が階段を歩いてのぼるときの速さの比を求めよ。
(2)太郎君は歩いて階段をのぼり始めた。次郎君は太郎君よりおくれてエスカレーターを歩いてのぼり始めると、同時に上の階に着いた。次郎君は太郎君が何段のぼったときにのぼり始めたか。
【数C】【空間ベクトル】(1) 2点A(5,-2,-3)、B(8,0,-4)を通る直線に垂線OHを下ろす。点Hの座標と線分OHの長さを求めよ。他1問

単元:
#空間ベクトル#空間ベクトル#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#空間ベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1) 2点A(5,-2,-3)、B(8,0,-4)を通る直線に、原点Oから垂線OHを下ろす。このとき、点Hの座標と線分OHの長さを求めよ。
(2) 2点A(0.-2,-3)、B(8,4,7)を通る直線に、点P(3,-1,4)から垂線PHを下ろす。このとき、点Hの座標と線分PHの長さを求めよ
この動画を見る
(1) 2点A(5,-2,-3)、B(8,0,-4)を通る直線に、原点Oから垂線OHを下ろす。このとき、点Hの座標と線分OHの長さを求めよ。
(2) 2点A(0.-2,-3)、B(8,4,7)を通る直線に、点P(3,-1,4)から垂線PHを下ろす。このとき、点Hの座標と線分PHの長さを求めよ
【受験算数】 S駅には150段のエスカレーターとその横に同じ段数の階段がある。太郎君がこのエスカレーターを歩いてのぼると100段のぼって上の階に着いた。また次郎君がこのエスカレーターを歩いてのぼると…

単元:
#算数(中学受験)#速さ#速さその他
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
S駅には150段のエスカレーターとその横に同じ段数の階段がある。太郎君がこのエスカレーターを歩いてのぼると、100段のぼって上の階に着いた。また、次郎君がこのエスカレーターを歩いてのぼると、上の階に着くまでの時間が太郎君より20%多くかかった。
(1)太郎君と次郎君が階段を歩いてのぼるときの速さの比を求めよ。
(2)太郎君は歩いて階段をのぼり始めた。次郎君は太郎君よりおくれてエスカレーターを歩いてのぼり始めると、同時に上の階に着いた。次郎君は太郎君が何段のぼったときにのぼり始めたか。
この動画を見る
S駅には150段のエスカレーターとその横に同じ段数の階段がある。太郎君がこのエスカレーターを歩いてのぼると、100段のぼって上の階に着いた。また、次郎君がこのエスカレーターを歩いてのぼると、上の階に着くまでの時間が太郎君より20%多くかかった。
(1)太郎君と次郎君が階段を歩いてのぼるときの速さの比を求めよ。
(2)太郎君は歩いて階段をのぼり始めた。次郎君は太郎君よりおくれてエスカレーターを歩いてのぼり始めると、同時に上の階に着いた。次郎君は太郎君が何段のぼったときにのぼり始めたか。
【高校物理】PーVグラフ:一定量の理想気体の状態を、図の矢印の順にゆっくりと変化させた。(1) CD間は、温度が一定の変化である。CD間での圧力pと体積Vとの関係を式で示せ。(2) CD間の温度を9…

単元:
#物理#熱・波・音#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
一定量の理想気体の状態を、図の矢印の順にゆっくりと変化させた。
(1) CD間は、温度が一定の変化である。CD間での圧力pと体積Vとの関係を式で示せ。
(2) CD間の温度を9.0x10^2Kとすると、A,Bの温度はそれぞれ何Kか。
この動画を見る
一定量の理想気体の状態を、図の矢印の順にゆっくりと変化させた。
(1) CD間は、温度が一定の変化である。CD間での圧力pと体積Vとの関係を式で示せ。
(2) CD間の温度を9.0x10^2Kとすると、A,Bの温度はそれぞれ何Kか。
【受験算数】 A地点とB地点を結ぶ動く歩道がある。お父さんと聖君はA地点を同時に出発し、動く歩道を利用してB地点まで歩いたところ、お父さんは320歩で歩き、聖君はお父さんより24秒遅れて着いた…

単元:
#算数(中学受験)#速さ#速さその他
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
A地点とB地点を結ぶ動く歩道がある。お父さんと聖君はA地点を同時に出発し、動く歩道を利用してB地点まで歩いたところ、お父さんは320歩で歩き、聖君はお父さんより24秒遅れて着いた。お父さんが、A地点からB地点まで動く歩道を利用しないで歩くと480歩で着く。なお、お父さんと聖君は2人とも歩く速さは一定で、歩幅はそれぞれ50cm、25cm。また、お父さんが2歩進む間に聖君は3歩進む。
(1)A地点からB地点までの距離は何mか。
(2)動く歩道を利用しないでお父さんが歩く速さと、動く歩道の進む速さの比を求めよ。
(3)動く歩道を利用しないとき、お父さんが歩く速さと聖君が歩く速さの比を求めよ。
(4)動く歩道の進む速さは毎分何mか。
この動画を見る
A地点とB地点を結ぶ動く歩道がある。お父さんと聖君はA地点を同時に出発し、動く歩道を利用してB地点まで歩いたところ、お父さんは320歩で歩き、聖君はお父さんより24秒遅れて着いた。お父さんが、A地点からB地点まで動く歩道を利用しないで歩くと480歩で着く。なお、お父さんと聖君は2人とも歩く速さは一定で、歩幅はそれぞれ50cm、25cm。また、お父さんが2歩進む間に聖君は3歩進む。
(1)A地点からB地点までの距離は何mか。
(2)動く歩道を利用しないでお父さんが歩く速さと、動く歩道の進む速さの比を求めよ。
(3)動く歩道を利用しないとき、お父さんが歩く速さと聖君が歩く速さの比を求めよ。
(4)動く歩道の進む速さは毎分何mか。
【数C】【空間ベクトル】四面体OABCにおいて、OA=OB、→OC⊥→ABとする。(1) AC=BCであることを証明せよ(2) 三角形ABCの重心をGとするとき、→OG⊥→ABであることを証明せよ

単元:
#空間ベクトル#空間ベクトル#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#空間ベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
四面体OABCにおいて、OA=OB、
OC⊥ABとする。
(1) AC=BCであることを証明せよ
(2) 三角形ABCの重心をGとするとき、OG⊥ABであることを証明せよ
この動画を見る
四面体OABCにおいて、OA=OB、
OC⊥ABとする。
(1) AC=BCであることを証明せよ
(2) 三角形ABCの重心をGとするとき、OG⊥ABであることを証明せよ
【中学受験理科】地質柱状図③:図2は、標高が同じである図1のA,B,C,E地点でボーリング調査をした結果を表しています。この結果をもとに、次の問に答えなさい。なお、すべての層は平行に堆積しています…

単元:
#理科(中学受験)#地学分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
図2は、標高が同じである図1のA,B,C,E地点でボーリング調査をした結果を表しています。この結果をもとに、次の問に答えなさい。なお、すべての層は平行に堆積しています
問1 この土地の地層は、どちらの方角へ下がっていますか。8方位で答えなさい
問2 D地点で火山灰の層が見られるのは、地表から何mの深さですか
問3 E地点の地質柱状図をかきなさい
※表や図は動画内に記載
この動画を見る
図2は、標高が同じである図1のA,B,C,E地点でボーリング調査をした結果を表しています。この結果をもとに、次の問に答えなさい。なお、すべての層は平行に堆積しています
問1 この土地の地層は、どちらの方角へ下がっていますか。8方位で答えなさい
問2 D地点で火山灰の層が見られるのは、地表から何mの深さですか
問3 E地点の地質柱状図をかきなさい
※表や図は動画内に記載
【高校物理】池の底の泡:深さ4.0m、7.0℃の池の底で発生した泡が、27℃,1.0気圧の水面まで上昇するとき、その体積は最初の何倍になるか。ただし,水中では、10m深くなるごとに圧力は1.0気圧ず…

単元:
#物理#熱・波・音#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
深さ4.0m、7.0℃の池の底で発生した泡が、27℃,1.0気圧の水面まで上昇するとき、その体積は最初の何倍になるか。ただし,水中では、10m深くなるごとに圧力は1.0気圧ずつ増加し、泡に含まれる気体の温度は周囲と常に等しいとする。
この動画を見る
深さ4.0m、7.0℃の池の底で発生した泡が、27℃,1.0気圧の水面まで上昇するとき、その体積は最初の何倍になるか。ただし,水中では、10m深くなるごとに圧力は1.0気圧ずつ増加し、泡に含まれる気体の温度は周囲と常に等しいとする。
【受験算数】 A地点とB地点を結ぶ動く歩道がある。お父さんと聖君はA地点を同時に出発し、動く歩道を利用してB地点まで歩いたところ、お父さんは360歩で歩き、聖君はお父さんより90秒遅れて着いた…

単元:
#算数(中学受験)#速さ#速さその他
教材:
#SPX#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
A地点とB地点を結ぶ動く歩道がある。お父さんと聖君はA地点を同時に出発し、動く歩道を利用してB地点まで歩いたところ、お父さんは360歩で歩き、聖君はお父さんより90秒遅れて着いた。お父さんが、A地点からB地点まで動く歩道を利用しないで歩くと420歩で着く。なお、お父さんと聖君は2人とも歩く速さは一定で、歩幅はそれぞれ75cm、45cm。また、お父さんが9歩進む間に聖君は10歩進む。
(1)A地点からB地点までの距離は何mか。
(2)動く歩道を利用しないでお父さんが歩く速さと、動く歩道の進む速さの比を求めよ。
(3)動く歩道を利用しないとき、お父さんが歩く速さと聖君が歩く速さの比を求めよ。
(4)動く歩道の進む速さは毎分何mか。
この動画を見る
A地点とB地点を結ぶ動く歩道がある。お父さんと聖君はA地点を同時に出発し、動く歩道を利用してB地点まで歩いたところ、お父さんは360歩で歩き、聖君はお父さんより90秒遅れて着いた。お父さんが、A地点からB地点まで動く歩道を利用しないで歩くと420歩で着く。なお、お父さんと聖君は2人とも歩く速さは一定で、歩幅はそれぞれ75cm、45cm。また、お父さんが9歩進む間に聖君は10歩進む。
(1)A地点からB地点までの距離は何mか。
(2)動く歩道を利用しないでお父さんが歩く速さと、動く歩道の進む速さの比を求めよ。
(3)動く歩道を利用しないとき、お父さんが歩く速さと聖君が歩く速さの比を求めよ。
(4)動く歩道の進む速さは毎分何mか。
【数C】【空間ベクトル】四面体ABCDにおいて、次のことを証明せよ。(1) →AB・→AC=→AC・→AD=→AD・→AB(2) AB⊥CD

単元:
#空間ベクトル#空間ベクトル#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#空間ベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
正四面体 $\mathrm{ABCD}$ において、次のことを証明せよ。
(1) $\vec{\mathrm{AB}}\cdot\vec{\mathrm{AC}} = \vec{\mathrm{AC}}\cdot\vec{\mathrm{AD}} = \vec{\mathrm{AD}}\cdot\vec{\mathrm{AB}}$
(2) $\mathrm{AB}\perp\mathrm{CD}$
この動画を見る
正四面体 $\mathrm{ABCD}$ において、次のことを証明せよ。
(1) $\vec{\mathrm{AB}}\cdot\vec{\mathrm{AC}} = \vec{\mathrm{AC}}\cdot\vec{\mathrm{AD}} = \vec{\mathrm{AD}}\cdot\vec{\mathrm{AB}}$
(2) $\mathrm{AB}\perp\mathrm{CD}$
【受験算数】ある品物に、仕入れ値の45%の利益を見込んで定価をつけました。しかし定価では売れなかったので定価の20%引きにしたところ品物は売れて利益は80円になりました。この品物の仕入れ値は何円ですか

単元:
#算数(中学受験)#文章題#売買損益と食塩水
教材:
#予習シ#予習シ算数・小5上#中学受験教材#食塩水
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある品物に、仕入れ値の45%の利益を見込んで定価をつけました。しかし、定価では売れなかったので定価の20%引きにしたところ、品物は売れて利益は80円になりました。この品物の仕入れ値は何円ですか。
この動画を見る
ある品物に、仕入れ値の45%の利益を見込んで定価をつけました。しかし、定価では売れなかったので定価の20%引きにしたところ、品物は売れて利益は80円になりました。この品物の仕入れ値は何円ですか。
【高校物理】弦の振動:振動数2.0✕10^2Hzのおんさの先端に、図のように糸を取りつけ、滑車を通しておもりAをつるした。PQの長さを0.90mとしておんさを振動させたところ、腹が3個の定常波が生じ…

単元:
#物理#熱・波・音#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
振動数2.0✕10^2Hzのおんさの先端に、図のように糸を取りつけ、滑車を通しておもりAをつるした。PQの長さを0.90mとしておんさを振動させたところ、腹が3個の定常波が生じた。
(1) 定常波の波長と糸を伝わる横波の速さは、それぞれいくらか。
(2) 滑車を移動させ、PQの長さを1.2mにすると、定常波の腹の数はいくらになるか。
(3) PQをもとの長さにもどし、Aを別のおもりBにすると、腹が2個の定常波ができた。このときの糸を伝わる横波の速さはいくらか。
この動画を見る
振動数2.0✕10^2Hzのおんさの先端に、図のように糸を取りつけ、滑車を通しておもりAをつるした。PQの長さを0.90mとしておんさを振動させたところ、腹が3個の定常波が生じた。
(1) 定常波の波長と糸を伝わる横波の速さは、それぞれいくらか。
(2) 滑車を移動させ、PQの長さを1.2mにすると、定常波の腹の数はいくらになるか。
(3) PQをもとの長さにもどし、Aを別のおもりBにすると、腹が2個の定常波ができた。このときの糸を伝わる横波の速さはいくらか。
【受験算数】13%の食塩水300gと7%の食塩水を混ぜて11%の食塩水を作ります。7%の食塩水を何 g混ぜればよいですか。

単元:
#算数(中学受験)#文章題#売買損益と食塩水
教材:
#予習シ#予習シ算数・小5上#中学受験教材#食塩水
指導講師:
理数個別チャンネル
問題文全文(内容文):
13%の食塩水300gと7%の食塩水を混ぜて11%の食塩水を作ります。7%の食塩水を何 g混ぜればよいですか。
この動画を見る
13%の食塩水300gと7%の食塩水を混ぜて11%の食塩水を作ります。7%の食塩水を何 g混ぜればよいですか。
【数C】【空間ベクトル】a,bはベクトルとする。a=(3,4,0)とb=(0,x,-√7)のなす角が45°であるとき,xの値を求めよ。

単元:
#空間ベクトル#空間ベクトル#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#空間ベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\vec{a}=(3, \, 4, \, 0)$ と $\vec{b}=(0, \, x, \, -\sqrt{7})$ のなす角が $45^{\circ}$ であるとき、$x$ の値を求めよ。
この動画を見る
$\vec{a}=(3, \, 4, \, 0)$ と $\vec{b}=(0, \, x, \, -\sqrt{7})$ のなす角が $45^{\circ}$ であるとき、$x$ の値を求めよ。
【中学受験理科】地質柱状図②:図2は、図1の土地のA~Dでボーリング調査をした結果です。これについて、次の問に答えなさい。なお、この地域の地層は、すべて水平に堆積しています。また、すべての層は平行に…

単元:
#理科(中学受験)#地学分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
図2は、図1の土地のA~Dでボーリング調査をした結果です。これについて、次の問に答えなさい。なお、この地域の地層は、すべて水平に堆積しています。また、すべての層は平行に堆積しています
問1 B地点を何mほるとa-a'面になりますか
問2 火山灰の層の厚さは何mですか
問3 A地点の地質柱状図をかきなさい
※表や図は動画内に記載
この動画を見る
図2は、図1の土地のA~Dでボーリング調査をした結果です。これについて、次の問に答えなさい。なお、この地域の地層は、すべて水平に堆積しています。また、すべての層は平行に堆積しています
問1 B地点を何mほるとa-a'面になりますか
問2 火山灰の層の厚さは何mですか
問3 A地点の地質柱状図をかきなさい
※表や図は動画内に記載
【高校物理】 水の混合:熱容量 200J/Kの容器に、水150gを入れてしばらく放置したところ。その温度が20°Cになった。この中に70°Cの水100gを入れると、全体の温度は何°Cになるか。ただし…

単元:
#物理#熱・波・音#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
熱容量 200J/Kの容器に、水150gを入れてしばらく放置したところ。その温度が20°Cになった。この中に70°Cの水100gを入れると、全体の温度は何°Cになるか。ただし、外部と熱のやりとりはなく、水の比熱を4.2J/(g・K)とする。
この動画を見る
熱容量 200J/Kの容器に、水150gを入れてしばらく放置したところ。その温度が20°Cになった。この中に70°Cの水100gを入れると、全体の温度は何°Cになるか。ただし、外部と熱のやりとりはなく、水の比熱を4.2J/(g・K)とする。
【受験算数】12%の食塩水が150gあります。この食塩水を何gか捨ててから、捨てた食塩水と同じ重さの水を加えたところ、8%の食塩水になりました。捨てた食塩水は何gですか。

単元:
#算数(中学受験)#文章題#売買損益と食塩水
教材:
#予習シ#予習シ算数・小5上#中学受験教材#食塩水
指導講師:
理数個別チャンネル
問題文全文(内容文):
12%の食塩水が150gあります。この食塩水を何gか捨ててから、捨てた食塩水と同じ重さの水を加えたところ、8%の食塩水になりました。捨てた食塩水は何gですか。
この動画を見る
12%の食塩水が150gあります。この食塩水を何gか捨ててから、捨てた食塩水と同じ重さの水を加えたところ、8%の食塩水になりました。捨てた食塩水は何gですか。
【数C】【空間ベクトル】4点A(1,1,2)、B(0,-4,0)、C(-1,1,-2)、D(2,3,5)がある。線分AB,AC,ADを3辺とする平行六面体の他の頂点の座標を求めよ。

単元:
#空間ベクトル#空間ベクトル#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#空間ベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
4点A(1,1,2)、B(0,-4,0)、C(-1,1,-2)、D(2,3,5)がある。線分AB,AC,ADを3辺とする平行六面体の他の頂点の座標を求めよ。
この動画を見る
4点A(1,1,2)、B(0,-4,0)、C(-1,1,-2)、D(2,3,5)がある。線分AB,AC,ADを3辺とする平行六面体の他の頂点の座標を求めよ。
【中学受験理科】地質柱状図①:図2は、図1のA,B,C,E地点でボーリング調査をした結果を表しています。この結果をもとに、次の問に答えなさい。なお、すべての地層は水平に堆積しています…

単元:
#理科(中学受験)#地学分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
図2は、図1のA,B,C,E地点でボーリング調査をした結果を表しています。この結果をもとに、次の問に答えなさい。なお、すべての地層は水平に堆積しています
問1 この地域の地層は、どちらの方角からどちらの方角へ、100mにつき何m下がっていますか
問2 D地点で火山灰の層が見られるのは、地表から何mの深さですか
問3 E地点の地質柱状図をかきなさい
※表や図は動画内に記載
この動画を見る
図2は、図1のA,B,C,E地点でボーリング調査をした結果を表しています。この結果をもとに、次の問に答えなさい。なお、すべての地層は水平に堆積しています
問1 この地域の地層は、どちらの方角からどちらの方角へ、100mにつき何m下がっていますか
問2 D地点で火山灰の層が見られるのは、地表から何mの深さですか
問3 E地点の地質柱状図をかきなさい
※表や図は動画内に記載
【高校物理】比熱と熱容量: 質量200gの鉄製の容器に、水150gが入っている。鉄の比熱を0.45J/(g・K),水の比熱を4.2J/(g・K)として、次の各問に答えよ。(1)鉄製の容器の熱容量はい…

単元:
#物理#熱・波・音#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
質量200gの鉄製の容器に、水150gが入っている。鉄の比熱を0.45J/(g・K)、水の比熱を4.2J/(g・K)として、次の各問に答えよ。
(1)鉄製の容器の熱容量はいくらか。
(2)全体の温度を1K上昇させるのに必要な熱量はいくらか。
(3)1800Jの熱量を与えたとき、全体の温度は何K上昇するか。
この動画を見る
質量200gの鉄製の容器に、水150gが入っている。鉄の比熱を0.45J/(g・K)、水の比熱を4.2J/(g・K)として、次の各問に答えよ。
(1)鉄製の容器の熱容量はいくらか。
(2)全体の温度を1K上昇させるのに必要な熱量はいくらか。
(3)1800Jの熱量を与えたとき、全体の温度は何K上昇するか。
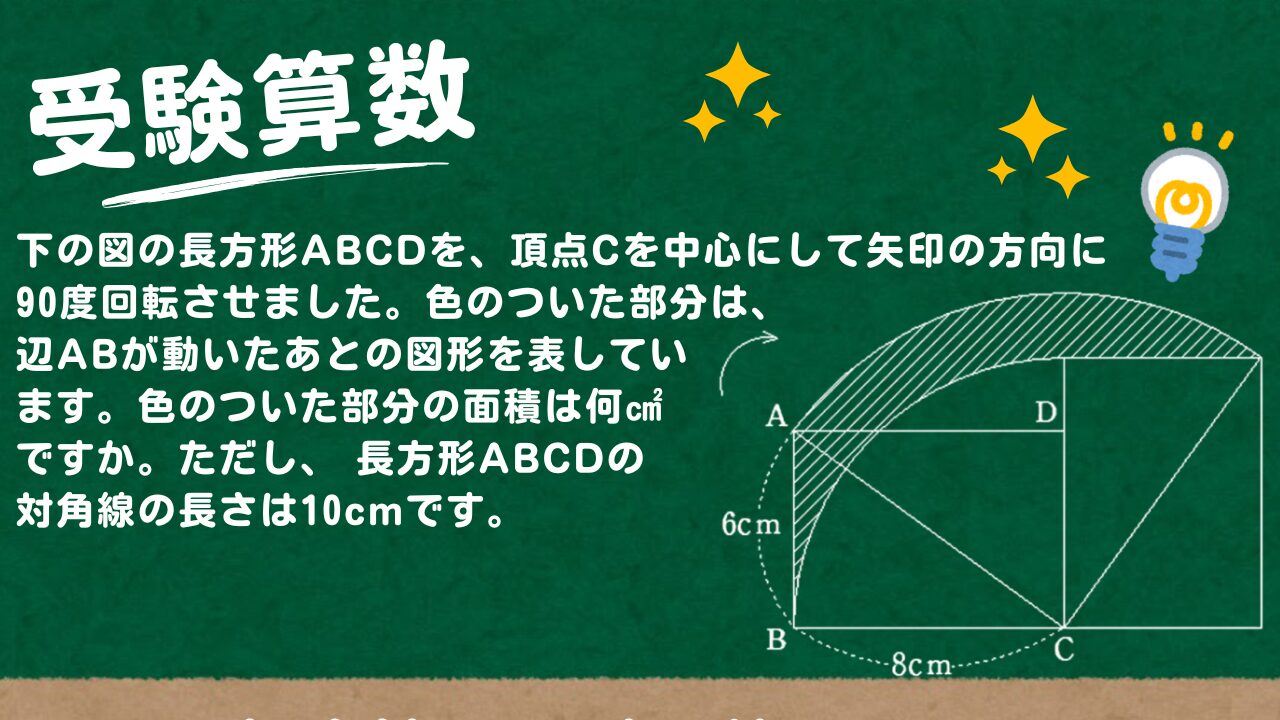
【受験算数】下の図の長方形ABCDを、頂点Cを中心にして矢印の方向に90度回転させました。色のついた部分は、辺ABが動いたあとの図形を表しています。色のついた部分の面積は何㎠ですか。
単元:
#算数(中学受験)#平面図形#図形の移動
教材:
#予習シ#予習シ算数・小5上#中学受験教材#平面図形
指導講師:
理数個別チャンネル
問題文全文(内容文):
下の図の長方形ABCDを、頂点Cを中心にして矢印の方向に90度回転させました。色のついた部分は、辺ABが動いたあとの図形を表しています。色のついた部分の面積は何㎠ですか。ただし、 長方形ABCDの対角線の長さは10cmです。
この動画を見る
下の図の長方形ABCDを、頂点Cを中心にして矢印の方向に90度回転させました。色のついた部分は、辺ABが動いたあとの図形を表しています。色のついた部分の面積は何㎠ですか。ただし、 長方形ABCDの対角線の長さは10cmです。
【数C】【空間ベクトル】a=(1,-1,-3)、b=(2,2,1)、c=(-1,-1,0)とする。|a+xb+yc|を最小にする実数x,yの値を求めよ。

単元:
#空間ベクトル#空間ベクトル#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#空間ベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
a,b,cをベクトルとする。a=(1,-1,-3)、b=(2,2,1)、c=(-1,-1,0)とする。|a+xb+yc|を最小にする実数x,yの値を求めよ。
この動画を見る
a,b,cをベクトルとする。a=(1,-1,-3)、b=(2,2,1)、c=(-1,-1,0)とする。|a+xb+yc|を最小にする実数x,yの値を求めよ。
【数C】【空間ベクトル】a=(0,1,2)、b=(2,4,6)とする。x=a+tb(tは実数)について、|x|の最小値を求めよ。また、その時のxを成分表示せよ。

単元:
#空間ベクトル#空間ベクトル#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#空間ベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
a,b,xをベクトルとする。
a=(0,1,2)、b=(2,4,6)とする。
x=a+tb(tは実数)について、|x|の最小値を求めよ。また、その時のxを成分表示せよ。
この動画を見る
a,b,xをベクトルとする。
a=(0,1,2)、b=(2,4,6)とする。
x=a+tb(tは実数)について、|x|の最小値を求めよ。また、その時のxを成分表示せよ。
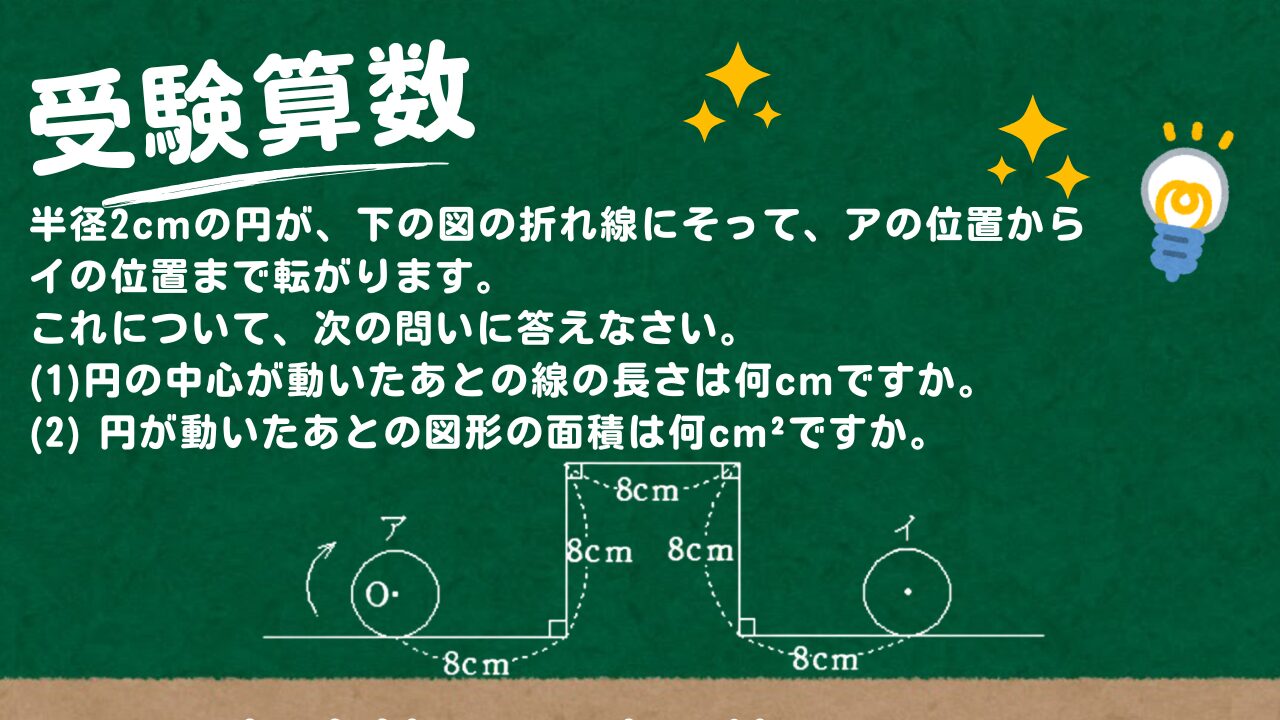
【受験算数】下半径2cmの円が、下の図の折れ線にそって、アの位置からイの位置まで転がります。これについて、次の問いに答えなさい。円の中心が動いたあとの線の長さは何cmですか。
単元:
#算数(中学受験)#平面図形#図形の移動
教材:
#予習シ#予習シ算数・小5上#中学受験教材#平面図形
指導講師:
理数個別チャンネル
問題文全文(内容文):
半径2cmの円が、下の図の折れ線にそって、アの位置からイの位置まで転がります。
これについて、次の問いに答えなさい。
(1)円の中心が動いたあとの線の長さは何cmですか。
(2) 円が動いたあとの図形の面積は何cm²ですか。
この動画を見る
半径2cmの円が、下の図の折れ線にそって、アの位置からイの位置まで転がります。
これについて、次の問いに答えなさい。
(1)円の中心が動いたあとの線の長さは何cmですか。
(2) 円が動いたあとの図形の面積は何cm²ですか。




