 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【受験算数】10から300までの整数を、次のように各位の数字を切り離して並べます。1,0,1,1,1,2,…,2,9,8,2,9,9,3,0,0 左から300番目の数字はいくつですか。

単元:
#算数(中学受験)#計算と数の性質#数の性質その他
教材:
#予習シ#予習シ・算数・小6上#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
10から300までの整数を、次のように各位の数字を切り離して並べます。
1,0,1,1,1,2,…,2,9,8,2,9,9,3,0,0
(1)左から300番目の数字はいくつですか。
(2)上の数列の中に、数字の「1」は何個ありますか。
この動画を見る
10から300までの整数を、次のように各位の数字を切り離して並べます。
1,0,1,1,1,2,…,2,9,8,2,9,9,3,0,0
(1)左から300番目の数字はいくつですか。
(2)上の数列の中に、数字の「1」は何個ありますか。
【高校化学】¹⁶₈O(質量数16陽子数8)、¹⁷₈O(質量数17陽子数8)、¹⁸₈O(質量数18陽子数8)について、陽子の数、中性子の数、電子の数をそれぞれ求めよ。

単元:
#化学#化学基礎1ー物質の構成#原子の構成と元素の周期表#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
天然の酸素原子には¹⁶₈O(質量数16陽子数8)、¹⁷₈O(質量数17陽子数8)、¹⁸₈O(質量数18陽子数8)がある。次の各問いに答えよ。
(1)これらの原子の関係を何というか。
(2)¹⁶₈O(質量数16陽子数8)、¹⁷₈O(質量数17陽子数8)、¹⁸₈O(質量数18陽子数8)について、陽子の数、中性子の数、電子の数をそれぞれ求めよ。
(3)これらの3種類の酸素原子を組み合わせると、何種類の酸素分子O₂ができるか。
この動画を見る
天然の酸素原子には¹⁶₈O(質量数16陽子数8)、¹⁷₈O(質量数17陽子数8)、¹⁸₈O(質量数18陽子数8)がある。次の各問いに答えよ。
(1)これらの原子の関係を何というか。
(2)¹⁶₈O(質量数16陽子数8)、¹⁷₈O(質量数17陽子数8)、¹⁸₈O(質量数18陽子数8)について、陽子の数、中性子の数、電子の数をそれぞれ求めよ。
(3)これらの3種類の酸素原子を組み合わせると、何種類の酸素分子O₂ができるか。
【受験算数】あるホテルの部屋番号は、数字の4を使った数をとばして、1号室、2号室、3号室、5号室、6号室…と順に番号がついています。たとえば、23号室の次は25号室、39号室の次は50号室です…

単元:
#算数(中学受験)#計算と数の性質#数の性質その他
教材:
#予習シ#予習シ・算数・小6上#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
あるホテルの部屋番号は、数字の4を使った数をとばして、1号室、2号室、3号室、5号室、6号室…と順に番号がついています。たとえば、23号室の次は25号室、39号室の次は50号室です。
(1)176号室は、はじめからかぞえて何番目の部屋ですか。
(2)はじめからかぞえて258番目の部屋は何号室ですか。
この動画を見る
あるホテルの部屋番号は、数字の4を使った数をとばして、1号室、2号室、3号室、5号室、6号室…と順に番号がついています。たとえば、23号室の次は25号室、39号室の次は50号室です。
(1)176号室は、はじめからかぞえて何番目の部屋ですか。
(2)はじめからかぞえて258番目の部屋は何号室ですか。
【中学受験理科】滑車①:問1 次の滑車の図について、①~⑧にあてはまる数字を答えなさい。なお、滑車の重さは考えないものとします。問2 図1~図8でおもりを10cm 動かすためには、それぞれひもを何cm

単元:
#理科(中学受験)#物理分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
問1 次の滑車の図について、①~⑧にあてはまる数字を答えなさい。なお、滑車の重さは考えないものとします。
問2 図1~図8でおもりを10cm 動かすためには、それぞれひもを何cm引けばよいですか。
この動画を見る
問1 次の滑車の図について、①~⑧にあてはまる数字を答えなさい。なお、滑車の重さは考えないものとします。
問2 図1~図8でおもりを10cm 動かすためには、それぞれひもを何cm引けばよいですか。
【高校物理】キルヒホッフの法則:図のように、内部抵抗の無視できる起電力がそれぞれ6.4V、 2.0Vの電池E₁、E₂、および抵抗値がそれぞれ5.0Ω、2.0Ω、4.0Ωの抵 抗 R₁、R₂、R₃を…

単元:
#物理#電気#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
図のように、内部抵抗の無視できる起電力がそれぞれ6.4V、 2.0Vの電池E₁、E₂、および抵抗値がそれぞれ5.0Ω、2.0Ω、4.0Ωの抵 抗 R₁、R₂、R₃を接続した。このとき、各抵抗を流れる電流の向きと大きさはいくらか。
この動画を見る
図のように、内部抵抗の無視できる起電力がそれぞれ6.4V、 2.0Vの電池E₁、E₂、および抵抗値がそれぞれ5.0Ω、2.0Ω、4.0Ωの抵 抗 R₁、R₂、R₃を接続した。このとき、各抵抗を流れる電流の向きと大きさはいくらか。
【高校化学】粒子の振動や直進などの運動を(ア)という。固体、液体、気体のいずれの状態でも構成粒子は(ア)をしており、(ア)の激しさは(イ)の状態が最も激しい(ア)によって空間に拡がっていく現象を(ウ)

単元:
#化学#化学基礎1ー物質の構成#物質の成分と構成元素#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の文中の( )に適当な語句、記号を入れよ。
粒子の振動や直進などの運動を( ア )という。固体、液体、気体のいずれの状態でも構成粒子は(ア)をしており、(ア)の激しさは( イ )の状態が最も激しい。構成粒子が、(ア)によって空間に拡がっていく現象を( ウ )という。
この動画を見る
次の文中の( )に適当な語句、記号を入れよ。
粒子の振動や直進などの運動を( ア )という。固体、液体、気体のいずれの状態でも構成粒子は(ア)をしており、(ア)の激しさは( イ )の状態が最も激しい。構成粒子が、(ア)によって空間に拡がっていく現象を( ウ )という。
【中学受験理科】光①:鏡について、次の問いに答えなさい。問1 次の図のように、鏡の前のX、A~Dの位置に人が立っています。Xの位置に立っている人が鏡を通じて見ることができる人の立っている位置を、A~D

単元:
#理科(中学受験)#物理分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
鏡について、次の問いに答えなさい。
問1 次の図のように、鏡の前のX、A~Dの位置に人が立っています。Xの位置に立っている人が鏡を通じて見ることができる人の立っている位置を、A~Dからすべて選び、記号で答えない。
問2 問1で、Xの位置に立っている人が、鏡を通じてA~Dの位置に立っている人をすべて見られるようにするためには、図の右方向に最後何m移動する必要がありますか。
この動画を見る
鏡について、次の問いに答えなさい。
問1 次の図のように、鏡の前のX、A~Dの位置に人が立っています。Xの位置に立っている人が鏡を通じて見ることができる人の立っている位置を、A~Dからすべて選び、記号で答えない。
問2 問1で、Xの位置に立っている人が、鏡を通じてA~Dの位置に立っている人をすべて見られるようにするためには、図の右方向に最後何m移動する必要がありますか。
【高校物理】電流と電子の速さ:断面積2.0×10-⁶m²のアルミニウムの導線に、4.8Aの電流が流れている。アルミニウム1m³ あたりの自由電子の数を6.0×10²³個、電子の電荷を…

単元:
#物理#電気#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
断面積2.0×10-⁶m²のアルミニウムの導線に、4.8Aの電流が流れている。
アルミニウム1m³ あたりの自由電子の数を6.0×10²³個、電子の電荷を -1.6×10⁻¹⁹Cとして、次の各問に答えよ。
(1) 導線の断面を1s間に通過する電子の数はいくらか。
(2) 電子が移動する平均の速さはいくらか。
この動画を見る
断面積2.0×10-⁶m²のアルミニウムの導線に、4.8Aの電流が流れている。
アルミニウム1m³ あたりの自由電子の数を6.0×10²³個、電子の電荷を -1.6×10⁻¹⁹Cとして、次の各問に答えよ。
(1) 導線の断面を1s間に通過する電子の数はいくらか。
(2) 電子が移動する平均の速さはいくらか。
【受験算数】右の図のような16個の空らんに0以上の整数を記入して、たて、横に加えた和が、らん外に記したA、1、1、1になるようにして表を作る。A=0とすると、この表は何通りできるか。

単元:
#算数(中学受験)#場合の数#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図のような16個の空らんに0以上の整数を記入して、たて、横に加えた和が、らん外に記したA、1、1、1になるようにして表を作る。
(1)A=0とすると、この表は何通りできるか。
(2)A=1とすると、この表は何通りできるか。
(3)A=2とすると、この表は何通りできるか。
(4)A=3とすると、この表は何通りできるか。
この動画を見る
右の図のような16個の空らんに0以上の整数を記入して、たて、横に加えた和が、らん外に記したA、1、1、1になるようにして表を作る。
(1)A=0とすると、この表は何通りできるか。
(2)A=1とすると、この表は何通りできるか。
(3)A=2とすると、この表は何通りできるか。
(4)A=3とすると、この表は何通りできるか。
【解答速報・全問解説】2026年 神奈川大学給費生試験 化学解答速報【化学のタカシー】

単元:
#化学#大学入試過去問(化学)#理科(高校生)#神奈川大学#大学入試解答速報#化学#神奈川大学
指導講師:
理数個別チャンネル
問題文全文(内容文):
著作権の関係で問題を映せないため、お手元に問題をご用意した上でご覧ください。
こちらの動画は、2025年12月21日(日)に実施された、2026年神奈川大学給費生試験の化学の解答速報です。著作権の関係で問題を映せないため、お手元に問題をご用意した上でご覧ください。
当チャンネル講師が独自に行っている解説なので、解答の誤りなどがある場合がございます。その場合はご了承ください。必ず公式に発表される解答をご確認ください。
この動画を見る
著作権の関係で問題を映せないため、お手元に問題をご用意した上でご覧ください。
こちらの動画は、2025年12月21日(日)に実施された、2026年神奈川大学給費生試験の化学の解答速報です。著作権の関係で問題を映せないため、お手元に問題をご用意した上でご覧ください。
当チャンネル講師が独自に行っている解説なので、解答の誤りなどがある場合がございます。その場合はご了承ください。必ず公式に発表される解答をご確認ください。
【解答速報・全問解説】2026年 神奈川大学給費生試験 文系数学解答速報【秋山先生】

単元:
#大学入試解答速報#数学#神奈川大学
指導講師:
理数個別チャンネル
問題文全文(内容文):
著作権の関係で問題を映せないため、お手元に問題をご用意した上でご覧ください。
こちらの動画は、2025年12月21日(日)に実施された、2026年神奈川大学給費生試験の文系数学の解答速報です。著作権の関係で問題を映せないため、お手元に問題をご用意した上でご覧ください。
当チャンネル講師が独自に行っている解説なので、解答の誤りなどがある場合がございます。その場合はご了承ください。必ず公式に発表される解答をご確認ください。
この動画を見る
著作権の関係で問題を映せないため、お手元に問題をご用意した上でご覧ください。
こちらの動画は、2025年12月21日(日)に実施された、2026年神奈川大学給費生試験の文系数学の解答速報です。著作権の関係で問題を映せないため、お手元に問題をご用意した上でご覧ください。
当チャンネル講師が独自に行っている解説なので、解答の誤りなどがある場合がございます。その場合はご了承ください。必ず公式に発表される解答をご確認ください。
【解答速報・全問解説】2026年 神奈川大学給費生試験 理系数学解答速報【理数大明神】

単元:
#大学入試解答速報#数学#神奈川大学
指導講師:
理数個別チャンネル
問題文全文(内容文):
著作権の関係で問題を映せないため、お手元に問題をご用意した上でご覧ください。
こちらの動画は、2025年12月21日(日)に実施された、2026年神奈川大学給費生試験の理系数学の解答速報です。著作権の関係で問題を映せないため、お手元に問題をご用意した上でご覧ください。
当チャンネル講師が独自に行っている解説なので、解答の誤りなどがある場合がございます。その場合はご了承ください。必ず公式に発表される解答をご確認ください。
この動画を見る
著作権の関係で問題を映せないため、お手元に問題をご用意した上でご覧ください。
こちらの動画は、2025年12月21日(日)に実施された、2026年神奈川大学給費生試験の理系数学の解答速報です。著作権の関係で問題を映せないため、お手元に問題をご用意した上でご覧ください。
当チャンネル講師が独自に行っている解説なので、解答の誤りなどがある場合がございます。その場合はご了承ください。必ず公式に発表される解答をご確認ください。
【解答速報・全問解説】2026年 神奈川大学給費生試験 英語解答速報【ゆう☆たろう】

単元:
#大学入試解答速報#英語#神奈川大学
指導講師:
理数個別チャンネル
問題文全文(内容文):
こちらの動画は、2025年12月21日(日)に実施された、2026年神奈川大学給費生試験の英語の解答速報です。著作権の関係で問題を映せないため、お手元に問題をご用意した上でご覧ください。
当チャンネル講師が独自に行っている解説なので、解答の誤りなどがある場合がございます。その場合はご了承ください。必ず公式に発表される解答をご確認ください。
この動画を見る
こちらの動画は、2025年12月21日(日)に実施された、2026年神奈川大学給費生試験の英語の解答速報です。著作権の関係で問題を映せないため、お手元に問題をご用意した上でご覧ください。
当チャンネル講師が独自に行っている解説なので、解答の誤りなどがある場合がございます。その場合はご了承ください。必ず公式に発表される解答をご確認ください。
【解答速報・全問解説】2026年 神奈川大学給費生試験 物理解答速報【NI・SHI・NO】

単元:
#大学入試解答速報#物理#神奈川大学
指導講師:
理数個別チャンネル
問題文全文(内容文):
著作権の関係で問題を映せないため、お手元に問題をご用意した上でご覧ください。
こちらの動画は、2025年12月21日(日)に実施された、2026年神奈川大学給費生試験の物理の解答速報です。著作権の関係で問題を映せないため、お手元に問題をご用意した上でご覧ください。
当チャンネル講師が独自に行っている解説なので、解答の誤りなどがある場合がございます。その場合はご了承ください。必ず公式に発表される解答をご確認ください。
※訂正※
16:30頃に「4アンペアボルト」と話している場面がありますが、正しくは「4Iボルト」になります。
この動画を見る
著作権の関係で問題を映せないため、お手元に問題をご用意した上でご覧ください。
こちらの動画は、2025年12月21日(日)に実施された、2026年神奈川大学給費生試験の物理の解答速報です。著作権の関係で問題を映せないため、お手元に問題をご用意した上でご覧ください。
当チャンネル講師が独自に行っている解説なので、解答の誤りなどがある場合がございます。その場合はご了承ください。必ず公式に発表される解答をご確認ください。
※訂正※
16:30頃に「4アンペアボルト」と話している場面がありますが、正しくは「4Iボルト」になります。
【受験算数】何人かの生徒が、いすに横一列に座っている。これから座り方を変えようと思う。全員が今までとは異なるいすに座る座り方は何通りあるか。以下のそれぞれの人数の場合について答えよ。

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
何人かの生徒が、いすに横一列に座っている。これから座り方を変えようと思う。全員が今までとは異なるいすに座る座り方は何通りあるか。以下のそれぞれの人数の場合について答えよ。ただし、いすは人数と同じ数だけある。
(1)3人のとき。
(2)4人のとき。
(3)5人のとき。
この動画を見る
何人かの生徒が、いすに横一列に座っている。これから座り方を変えようと思う。全員が今までとは異なるいすに座る座り方は何通りあるか。以下のそれぞれの人数の場合について答えよ。ただし、いすは人数と同じ数だけある。
(1)3人のとき。
(2)4人のとき。
(3)5人のとき。
【受験算数】点Oを中心とする円がある。この円の周囲を10等分する点をA,B,C,D,E,F,G,H,I,Jとする。これらの点にさらに点Oを加えた11個の点から、3つの点をとりだし、これらを頂点とする…

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
点Oを中心とする円がある。この円の周囲を10等分する点をA,B,C,D,E,F,G,H,I,Jとする。これらの点にさらに点Oを加えた11個の点から、3つの点をとりだし、これらを頂点とする三角形を作りたい。
(1)点Oを1つの頂点とする三角形は何個できるか。
(2)直角三角形は何個できるか。
(3)三角形は全部で何個作れるか。ただし、三角形ABFのように、三角形の一辺の上に点Oを含むものも、1つの三角形として数える。
この動画を見る
点Oを中心とする円がある。この円の周囲を10等分する点をA,B,C,D,E,F,G,H,I,Jとする。これらの点にさらに点Oを加えた11個の点から、3つの点をとりだし、これらを頂点とする三角形を作りたい。
(1)点Oを1つの頂点とする三角形は何個できるか。
(2)直角三角形は何個できるか。
(3)三角形は全部で何個作れるか。ただし、三角形ABFのように、三角形の一辺の上に点Oを含むものも、1つの三角形として数える。
【高校化学】次の各記述の下線部と状態変化の名称の組み合わせで、正しいものをすべて選べ。(ア)池にはった氷が、昼にはなくなっていた。 昇華(イ)戸外に干しておいた洗濯物が乾いた。 蒸発 (他)

単元:
#化学#化学基礎1ー物質の構成#物質の成分と構成元素#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の各記述の下線部と状態変化の名称の組み合わせで、正しいものをすべて選べ。
(ア)池にはった氷が、昼にはなくなっていた。 昇華
(イ)戸外に干しておいた洗濯物が乾いた。 蒸発
(ウ)アイスクリームの箱の中に入れておいたドライアイスがなくなった。 融解
(エ)熱いお茶を飲もうとしたら、眼鏡が曇った。 凝縮
(オ)冷凍庫の製氷皿に水でぬれた指で触れると、指がくっついた。 凝固
この動画を見る
次の各記述の下線部と状態変化の名称の組み合わせで、正しいものをすべて選べ。
(ア)池にはった氷が、昼にはなくなっていた。 昇華
(イ)戸外に干しておいた洗濯物が乾いた。 蒸発
(ウ)アイスクリームの箱の中に入れておいたドライアイスがなくなった。 融解
(エ)熱いお茶を飲もうとしたら、眼鏡が曇った。 凝縮
(オ)冷凍庫の製氷皿に水でぬれた指で触れると、指がくっついた。 凝固
【受験算数】点Oを中心とする円がある。この円の周囲を6等分する点をA,B,C,D,E,Fとする。これらの点にさらに点Oを加えた7個の点から、3つの点をとりだし、これらを頂点とする三角形を作る。正三角…

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
点Oを中心とする円がある。この円の周囲を6等分する点をA,B,C,D,E,Fとする。これらの点にさらに点Oを加えた7個の点から、3つの点をとりだし、これらを頂点とする三角形を作る。
(1)正三角形は何個できるか。
(2)点Oを1つの頂点とする三角形は何個できるか。
(3)直角三角形は何個できるか。
(4)三角形は全部で何個作れるか。ただし、三角形ABDのように、三角形の一辺の上に点Oを含むものも、1つの三角形として数える。
この動画を見る
点Oを中心とする円がある。この円の周囲を6等分する点をA,B,C,D,E,Fとする。これらの点にさらに点Oを加えた7個の点から、3つの点をとりだし、これらを頂点とする三角形を作る。
(1)正三角形は何個できるか。
(2)点Oを1つの頂点とする三角形は何個できるか。
(3)直角三角形は何個できるか。
(4)三角形は全部で何個作れるか。ただし、三角形ABDのように、三角形の一辺の上に点Oを含むものも、1つの三角形として数える。
【数Ⅲ】【微分】 f(x+y)=f(x)f(y)-sinxsiny,f'(0)=0 のとき次を示せ。 (1)f(0)=1 (2)f'(x)=-sinx (3)-1≦f(x+1)-f(x)≦1

単元:
#微分とその応用#接線と法線・平均値の定理#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#微分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
微分可能な関数f(x)とすべての実数x,yについて次の等式が成り立っている。
f(x+y)=f(x)f(y)-sinxsiny,f'(0)=0
このとき、次のことが成り立つことを示せ。
(1)f(0)=1 (2)f'(x)=-sinx (3)-1≦f(x+1)-f(x)≦1
この動画を見る
微分可能な関数f(x)とすべての実数x,yについて次の等式が成り立っている。
f(x+y)=f(x)f(y)-sinxsiny,f'(0)=0
このとき、次のことが成り立つことを示せ。
(1)f(0)=1 (2)f'(x)=-sinx (3)-1≦f(x+1)-f(x)≦1
【中学受験理科】音③:次の表のような条件で、AB間をはじいて音の高さを調べました。次の問いに答えなさい。ただし、実験2・3・4では同じ高さの音が聞こえました。問1 弦の長さと音の高さの関係を調べるため

単元:
#理科(中学受験)#物理分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の表のような条件で、AB間をはじいて音の高さを調べました。次の問いに答えなさい。ただし、実験2・3・4では同じ高さの音が聞こえました。
問1 弦の長さと音の高さの関係を調べるためには、どの実験とどの実験を比べればよいですか。あるだけ答えなさい。
問2 実験5と実験6ではどちらの方が音が高いですか。
問3 太さ1mm、長さ30cmの弦をはじいたときの音の高さを実験1と同じにするためには、おもりは何個必要ですか。
この動画を見る
次の表のような条件で、AB間をはじいて音の高さを調べました。次の問いに答えなさい。ただし、実験2・3・4では同じ高さの音が聞こえました。
問1 弦の長さと音の高さの関係を調べるためには、どの実験とどの実験を比べればよいですか。あるだけ答えなさい。
問2 実験5と実験6ではどちらの方が音が高いですか。
問3 太さ1mm、長さ30cmの弦をはじいたときの音の高さを実験1と同じにするためには、おもりは何個必要ですか。
【受験算数】たて2cm、横3cmの長方形がある。その周上に10個の点A,B,C,・・・,Jがあり、となりの点と点の間の長さは1cmとする。これら10個の点から適当に3点を選び、三角形を作る。例えば…
単元:
#算数(中学受験)#場合の数#場合の数
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
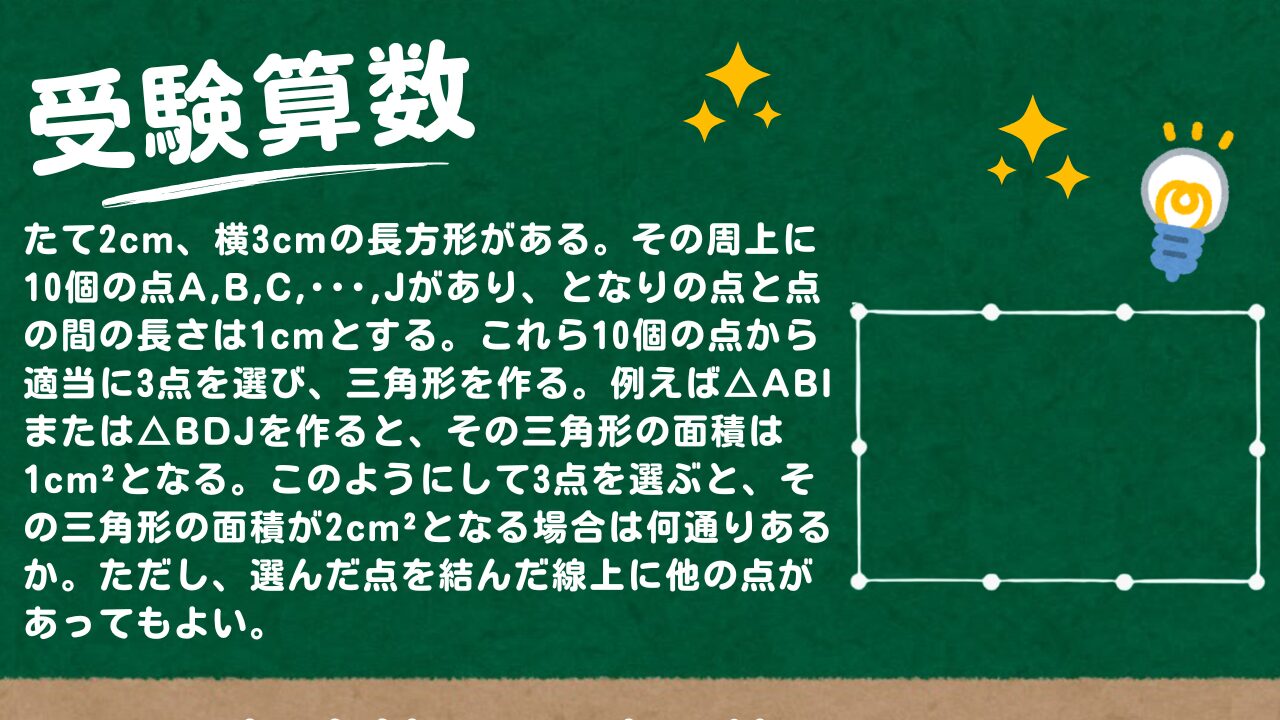
たて2cm、横3cmの長方形がある。その周上に10個の点A,B,C,・・・,Jがあり、となりの点と点の間の長さは1cmとする。これら10個の点から適当に3点を選び、三角形を作る。例えば△ABIまたは△BDJを作ると、その三角形の面積は1cm²となる。このようにして3点を選ぶと、その三角形の面積が2cm²となる場合は何通りあるか。ただし、選んだ点を結んだ線上に他の点があってもよい。
この動画を見る
たて2cm、横3cmの長方形がある。その周上に10個の点A,B,C,・・・,Jがあり、となりの点と点の間の長さは1cmとする。これら10個の点から適当に3点を選び、三角形を作る。例えば△ABIまたは△BDJを作ると、その三角形の面積は1cm²となる。このようにして3点を選ぶと、その三角形の面積が2cm²となる場合は何通りあるか。ただし、選んだ点を結んだ線上に他の点があってもよい。
【高校物理】電気量の変化:図のように、極板の間隔がdで、電気 容量が3×10⁻⁸Fの平行板コンデンサーに、10Vの電池を接続する。次の各問に答えよ。(1) コンデンサーにたくわえられる電荷はいくらか…

単元:
#物理#電気#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
図のように、極板の間隔がdで、電気 容量が3×10⁻⁸Fの平行板コンデンサーに、10Vの電池を接続する。次の各問に答えよ。
(1) コンデンサーにたくわえられる電荷はいくらか。
(2) 電池を接続したまま極板の間隔を3dに広げた。このとき、検流計を何Cの正電荷がどちら向きに移動するか。
向きは図のa、bの記号を用いて答えよ。
この動画を見る
図のように、極板の間隔がdで、電気 容量が3×10⁻⁸Fの平行板コンデンサーに、10Vの電池を接続する。次の各問に答えよ。
(1) コンデンサーにたくわえられる電荷はいくらか。
(2) 電池を接続したまま極板の間隔を3dに広げた。このとき、検流計を何Cの正電荷がどちら向きに移動するか。
向きは図のa、bの記号を用いて答えよ。
【受験算数】たて2cm、横4cmの長方形がある。その周上に12個の点A,B,C,・・・,Lがあり、となりの点と点の間の長さは1cm。これら12個の点から適当に3点を選び、三角形を作る。例えば△ACE…
単元:
#算数(中学受験)#場合の数#場合の数
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
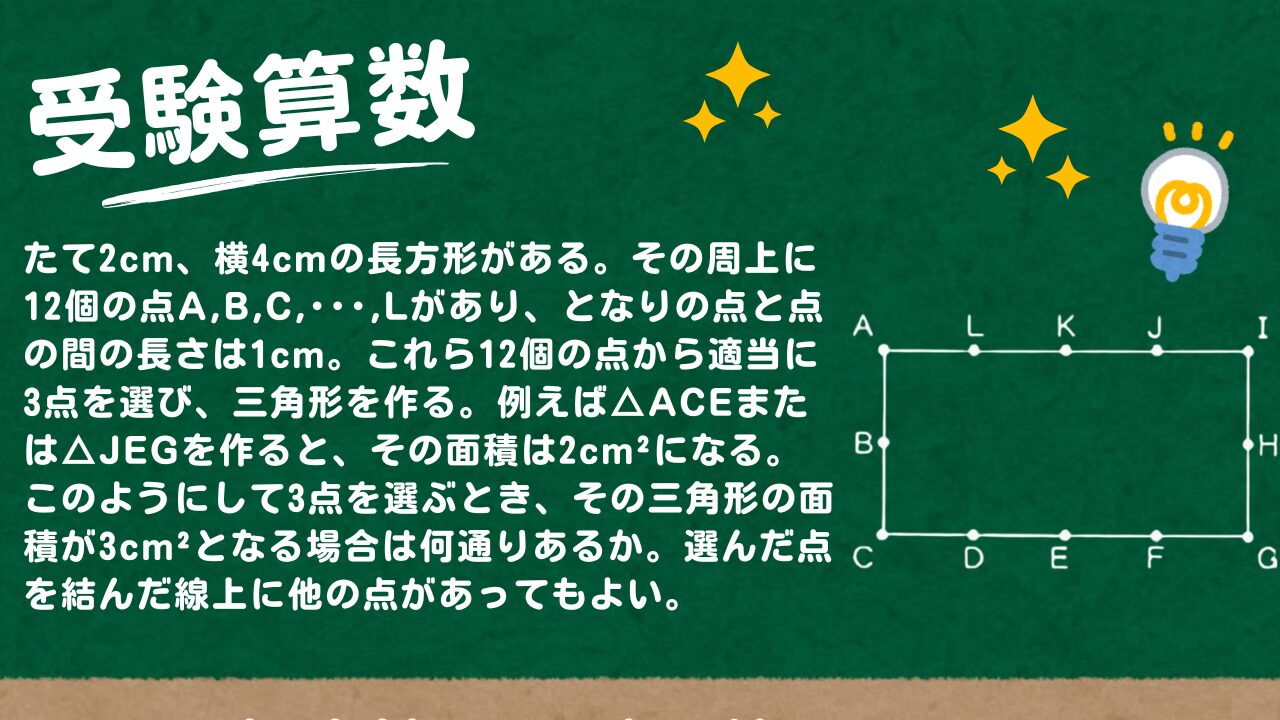
たて2cm、横4cmの長方形がある。その周上に12個の点A,B,C,・・・,Lがあり、となりの点と点の間の長さは1cm。これら12個の点から適当に3点を選び、三角形を作る。例えば△ACEまたは△JEGを作ると、その面積は2cm²になる。このようにして3点を選ぶとき、その三角形の面積が3cm²となる場合は何通りあるか。選んだ点を結んだ線上に他の点があってもよい。
この動画を見る
たて2cm、横4cmの長方形がある。その周上に12個の点A,B,C,・・・,Lがあり、となりの点と点の間の長さは1cm。これら12個の点から適当に3点を選び、三角形を作る。例えば△ACEまたは△JEGを作ると、その面積は2cm²になる。このようにして3点を選ぶとき、その三角形の面積が3cm²となる場合は何通りあるか。選んだ点を結んだ線上に他の点があってもよい。
【数Ⅲ】【関数】f(x)={0 (-1≦x≦1),|x|-1(x<-1,1<x), g(x)={x²-1(x<0), x-1(0≦x)で(gof)(x),(fog)(x)を求めよ。

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\begin{eqnarray}
f(x)
=
\begin{cases}
0 & ( -1 \leqq x \leqq 1 ) \\
|x|-1 & ( x < -1, 1 < x )
\end{cases}
\end{eqnarray}$
$\begin{eqnarray} g(x)
=
\begin{cases}
x^2-1 & ( x < 0 ) \\
x-1 & ( 0\leqq x )
\end{cases}
\end{eqnarray}$
であるとき、
$(g\circ f)(-3),(f\circ g)(-3),(g\circ f)(x),(f\circ g)(x)$
を求めよ。
この動画を見る
$\begin{eqnarray}
f(x)
=
\begin{cases}
0 & ( -1 \leqq x \leqq 1 ) \\
|x|-1 & ( x < -1, 1 < x )
\end{cases}
\end{eqnarray}$
$\begin{eqnarray} g(x)
=
\begin{cases}
x^2-1 & ( x < 0 ) \\
x-1 & ( 0\leqq x )
\end{cases}
\end{eqnarray}$
であるとき、
$(g\circ f)(-3),(f\circ g)(-3),(g\circ f)(x),(f\circ g)(x)$
を求めよ。
【中学受験理科】熱量②:表は、それぞれの物質1gの温度を1°C上昇させるのに必要な熱量です。これについて、次の問いに答えなさい。ただし、問3~問6では熱の移動は金属と水の間でしか行われないものとします

単元:
#理科(中学受験)#化学分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
表は、それぞれの物質1gの温度を1°C上昇させるのに必要な熱量です。これについて、次の問いに答えなさい。ただし、問3~問6では熱の移動は金属と水の間でしか行われないものとします。
問1 40°Cの湯 100gとある温度の湯50gを混ぜると50°Cになりました。ある温度とは何Cですか。
問2-20°Cの氷120gを0°Cの氷にするために必要な熱量は何カロリーですか。
問3 50°Cの水 120gに、130°Cに加熱した40gのアルミニウム球を入れると、55°Cになりました。
① アルミニウム球が失った熱量は何カロリーですか。
②アルミニウム18の温度を1で上昇させるのに必要な熱症は何カロリーですか。
問4 10°Cの水 90gに,200°Cに加熱した50gの鉄球を入れると何℃になりますか。
問5 30°Cの水50gに、300°Cに加熱した鉄球を入れると45°Cになりました。鉄球は何gですか。小数第2位を四捨五入して答えなさい。
問6 ある温度の水 40gに、90°Cに加熱した100gの鉄球を入れると、66°Cになりました。ある温度とは何°Cですか。
この動画を見る
表は、それぞれの物質1gの温度を1°C上昇させるのに必要な熱量です。これについて、次の問いに答えなさい。ただし、問3~問6では熱の移動は金属と水の間でしか行われないものとします。
問1 40°Cの湯 100gとある温度の湯50gを混ぜると50°Cになりました。ある温度とは何Cですか。
問2-20°Cの氷120gを0°Cの氷にするために必要な熱量は何カロリーですか。
問3 50°Cの水 120gに、130°Cに加熱した40gのアルミニウム球を入れると、55°Cになりました。
① アルミニウム球が失った熱量は何カロリーですか。
②アルミニウム18の温度を1で上昇させるのに必要な熱症は何カロリーですか。
問4 10°Cの水 90gに,200°Cに加熱した50gの鉄球を入れると何℃になりますか。
問5 30°Cの水50gに、300°Cに加熱した鉄球を入れると45°Cになりました。鉄球は何gですか。小数第2位を四捨五入して答えなさい。
問6 ある温度の水 40gに、90°Cに加熱した100gの鉄球を入れると、66°Cになりました。ある温度とは何°Cですか。
【受験算数】右の図は一辺1cmの正方形を並べたもの。この図のなかにはいろいろな大きさの長方形がある。長方形(ただし、正方形は除く)は全部で何個あるか。

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図は一辺1cmの正方形を並べたもの。
(1)この図のなかにはいろいろな大きさの正方形がある。正方形は全部で何個あるか。
(2)この図のなかにはいろいろな大きさの長方形がある。長方形(ただし、正方形は除く)は全部で何個あるか。
この動画を見る
右の図は一辺1cmの正方形を並べたもの。
(1)この図のなかにはいろいろな大きさの正方形がある。正方形は全部で何個あるか。
(2)この図のなかにはいろいろな大きさの長方形がある。長方形(ただし、正方形は除く)は全部で何個あるか。
【高校物理】電場と仕事:図は、正負等量の2つの点電荷がつくる電場の様子を、10V間隔の等電位線で表したものである。点Dの電位を0Vとし、電荷qを2.0Cの正の電気量をもつ点電荷とする。次の各問に答え…

単元:
#物理#電気#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
図は、正負等量の2つの点電荷がつくる電場の様子を、10V間隔の等電位線で表したものである。
点Dの電位を0Vとし、電荷qを2.0Cの正の電気量をもつ点電荷とする。次の各問に答えよ。
(1)点Bにおける電荷qの静電気力による位置エネルギーはいくらか。
(2)電荷qをA→B→C→Dの順にゆっくりと運ぶとき、外力が正の仕事をする区間はどれか。また、その仕事は何Jか。
(3)電場が電荷qに正の仕事をする区間はどれか。また、その仕事は何Jか。
(4)点D付近は、一様な電場とみなせる。電荷qを点Dに置いたとき、電荷qにはたらく静電気力の大きさと向きを求めよ。
この動画を見る
図は、正負等量の2つの点電荷がつくる電場の様子を、10V間隔の等電位線で表したものである。
点Dの電位を0Vとし、電荷qを2.0Cの正の電気量をもつ点電荷とする。次の各問に答えよ。
(1)点Bにおける電荷qの静電気力による位置エネルギーはいくらか。
(2)電荷qをA→B→C→Dの順にゆっくりと運ぶとき、外力が正の仕事をする区間はどれか。また、その仕事は何Jか。
(3)電場が電荷qに正の仕事をする区間はどれか。また、その仕事は何Jか。
(4)点D付近は、一様な電場とみなせる。電荷qを点Dに置いたとき、電荷qにはたらく静電気力の大きさと向きを求めよ。
【受験算数】 右の図は一辺1cmの正方形を並べたもの。この図のなかにはいろいろな大きさの正方形がある。正方形は全部で何個あるか。

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図は一辺1cmの正方形を並べたもの。
(1)この図のなかにはいろいろな大きさの正方形がある。正方形は全部で何個あるか。
(2)この図のなかにはいろいろな大きさの長方形がある。長方形(ただし、正方形は除く)は全部で何個あるか。
この動画を見る
右の図は一辺1cmの正方形を並べたもの。
(1)この図のなかにはいろいろな大きさの正方形がある。正方形は全部で何個あるか。
(2)この図のなかにはいろいろな大きさの長方形がある。長方形(ただし、正方形は除く)は全部で何個あるか。
【受験算数】3つの整数G、30、4の最大公約数は15,最小公倍数は450です。Gとして考えらえる整数をすべて答えなさい。

単元:
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題
教材:
#予習シ#予習シ・算数・小6上#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
3つの整数G、30、4の最大公約数は15,最小公倍数は450です。Gとして考えらえる整数をすべて答えなさい。
この動画を見る
3つの整数G、30、4の最大公約数は15,最小公倍数は450です。Gとして考えらえる整数をすべて答えなさい。
【英語】私立一貫校向け英語教材Lesson8--1 Stage3の英文解説

単元:
#英語(高校生)#英文法#否定表現・特別な表現
教材:
#NT ENGLISH SERIES#中高教材#Third Edition Stage3#Lesson8
指導講師:
理数個別チャンネル
問題文全文(内容文):
Tell me what you learned from this book.
I have no idea (as to) why the ancient city disappeared completely.
Why the city disappeared is a mystery, so experts are continuing their research.
The question is who ruled this city two thousand years ago.
What do you think the experts will do with the dinosaur fossils?
I think they will preserve them in a museum.
Who do you suppose is appropriate for the leader of our project?
I suppose Michael is.
この動画を見る
Tell me what you learned from this book.
I have no idea (as to) why the ancient city disappeared completely.
Why the city disappeared is a mystery, so experts are continuing their research.
The question is who ruled this city two thousand years ago.
What do you think the experts will do with the dinosaur fossils?
I think they will preserve them in a museum.
Who do you suppose is appropriate for the leader of our project?
I suppose Michael is.




