 数学を数楽に
数学を数楽に
 数学を数楽に
数学を数楽に
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
長方形と半円 気づけば一瞬!!

単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
長方形と半円
斜線部の面積=?
*図は動画内参照
この動画を見る
長方形と半円
斜線部の面積=?
*図は動画内参照
面積

単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
正方形
円の半径=5
赤線部の面積=?
*図は動画内参照
この動画を見る
正方形
円の半径=5
赤線部の面積=?
*図は動画内参照
不等式の応用 数I 大阪星光学院

単元:
#数学(中学生)#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
xについての不等式$5x+2 \leqq 4a$を満たす最大の整数が3ときaの値の範囲を求めよ。
大阪星光学院高等学校
この動画を見る
xについての不等式$5x+2 \leqq 4a$を満たす最大の整数が3ときaの値の範囲を求めよ。
大阪星光学院高等学校
3秒で答え出ます(剰余の定理)数II 割った余り
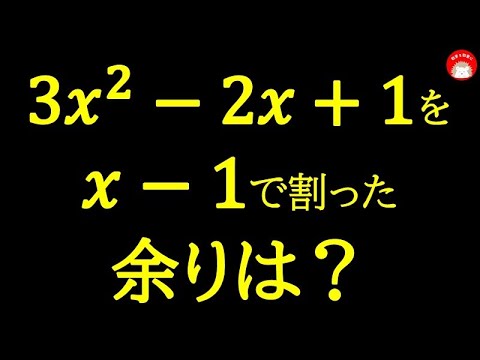
単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$3x^2-2x+1$をx-1で割った余りは?
この動画を見る
$3x^2-2x+1$をx-1で割った余りは?
部屋割り 組分け 他の問題もあり

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
部屋割り・グループ分け
(1)6人がAまたはBまたはCの3部屋に入る方法は何通り?
(1人も入らない部屋があってよい)
(2)6人を2つのグループに分ける方法は何通り?
(各グループは少なくとも2人以上)
(3)6人を3つのグループに分ける方法は何通り?
(各グループは少なくとも1人以上)
この動画を見る
部屋割り・グループ分け
(1)6人がAまたはBまたはCの3部屋に入る方法は何通り?
(1人も入らない部屋があってよい)
(2)6人を2つのグループに分ける方法は何通り?
(各グループは少なくとも2人以上)
(3)6人を3つのグループに分ける方法は何通り?
(各グループは少なくとも1人以上)
条件つき確率とは? 早稲田大学

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
5回に1回の割合で帽子を忘れる少女が3軒の家を訪れ帰宅後帽子を忘れたと気付いたとき2軒目に帽子を忘れる確率は?
早稲田大学
この動画を見る
5回に1回の割合で帽子を忘れる少女が3軒の家を訪れ帰宅後帽子を忘れたと気付いたとき2軒目に帽子を忘れる確率は?
早稲田大学
円周角 暁
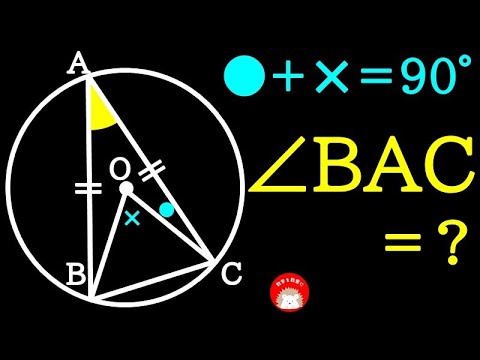
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
○+✖=90°
$\angle BAC=?$
*図は動画内参照
暁高等学校
この動画を見る
○+✖=90°
$\angle BAC=?$
*図は動画内参照
暁高等学校
平方根 式の値 國學院
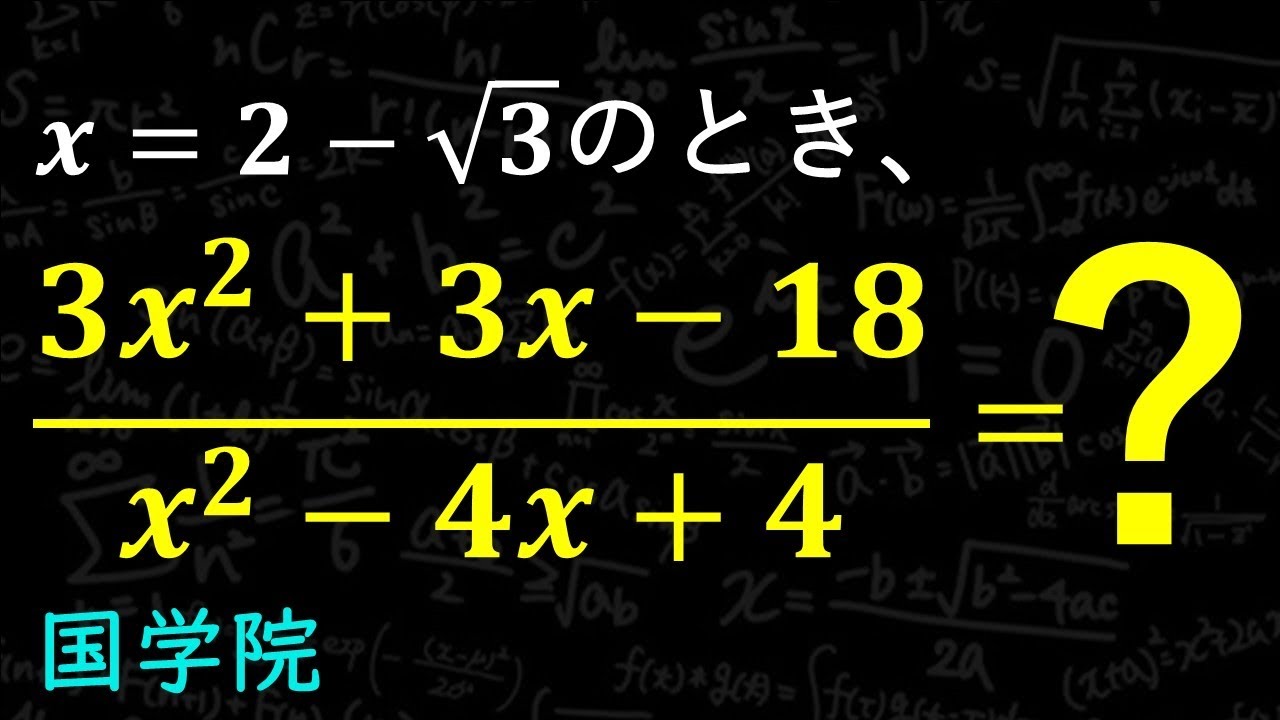
単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x=2-\sqrt 3$のとき
$\frac{3x^2+3x-18}{x^2-4x+4}$
國學院高等学校
この動画を見る
$x=2-\sqrt 3$のとき
$\frac{3x^2+3x-18}{x^2-4x+4}$
國學院高等学校
2次方程式の応用

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x^2-10x+\frac{a}{2} = 0$の解が奇数となるような正の整数aをすべて求めよ。
愛光高等学校
この動画を見る
$x^2-10x+\frac{a}{2} = 0$の解が奇数となるような正の整数aをすべて求めよ。
愛光高等学校
高評価か?低評価か?

加法定理の証明をベクトルで

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
cos(α+β)=cosαcosβ-sinαsinβ
cos(α-β)=cosαcosβ+sinαsinβ
cosα・cosβ+sinα・sinβ =
この動画を見る
cos(α+β)=cosαcosβ-sinαsinβ
cos(α-β)=cosαcosβ+sinαsinβ
cosα・cosβ+sinα・sinβ =
〇〇に注目すれば一瞬!3通りで解説
最短経路 他の問題もあり
単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
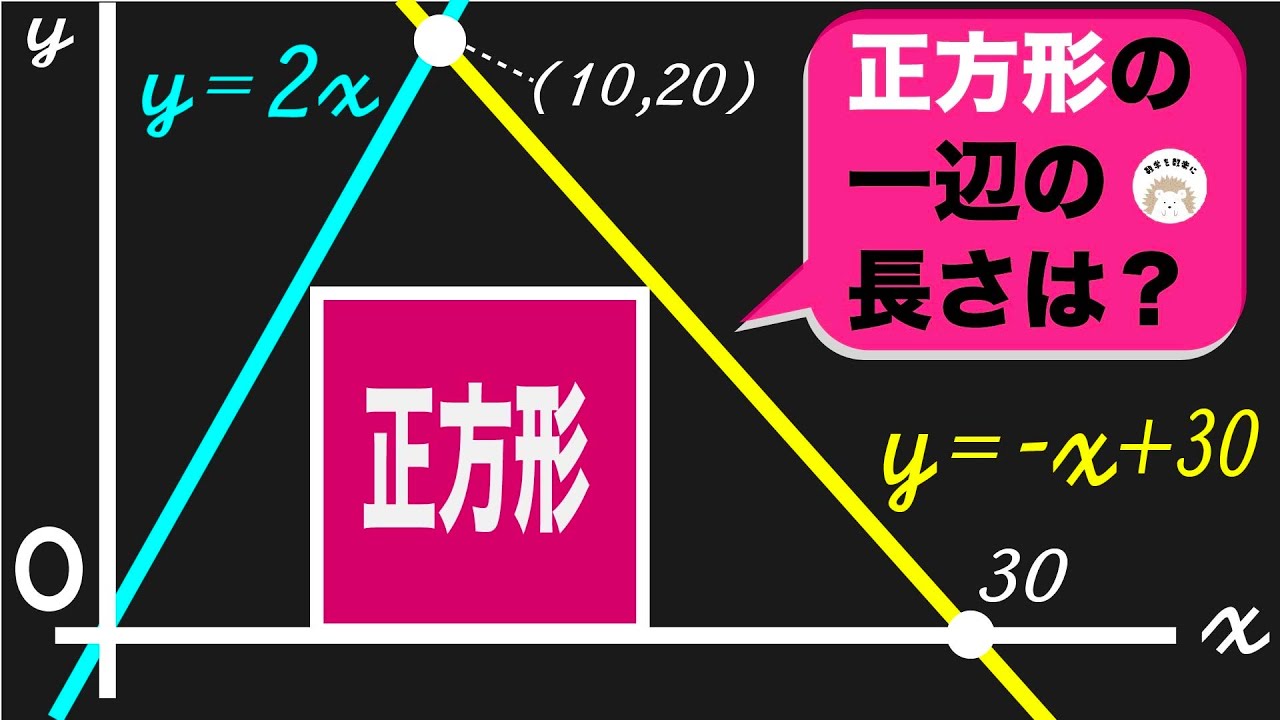
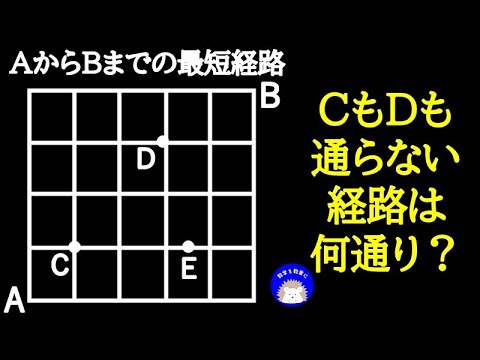
最短経路
AからBまで最短距離で行く。
(1)全部で何通り?
(2)Dを通らない場合は何通り?
(3)Eを通らない場合は何通り?
(4)CもDも通る場合は何通り?
(5)CもDも通らない場合は何通り?
この動画を見る
最短経路
AからBまで最短距離で行く。
(1)全部で何通り?
(2)Dを通らない場合は何通り?
(3)Eを通らない場合は何通り?
(4)CもDも通る場合は何通り?
(5)CもDも通らない場合は何通り?
整数問題 慶應義塾

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
a,b,cは1~9の異なる整数
$\frac{a+b+c}{abc}$の最大値は?
$\frac{a+b+c}{abc}$=
慶應義塾高等学校
この動画を見る
a,b,cは1~9の異なる整数
$\frac{a+b+c}{abc}$の最大値は?
$\frac{a+b+c}{abc}$=
慶應義塾高等学校
何をかけたら3乗になる?広陵

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
450をn倍するとある整数の3乗になった。
最も小さい自然数nは?
広陵高等学校
この動画を見る
450をn倍するとある整数の3乗になった。
最も小さい自然数nは?
広陵高等学校
角度を求める C
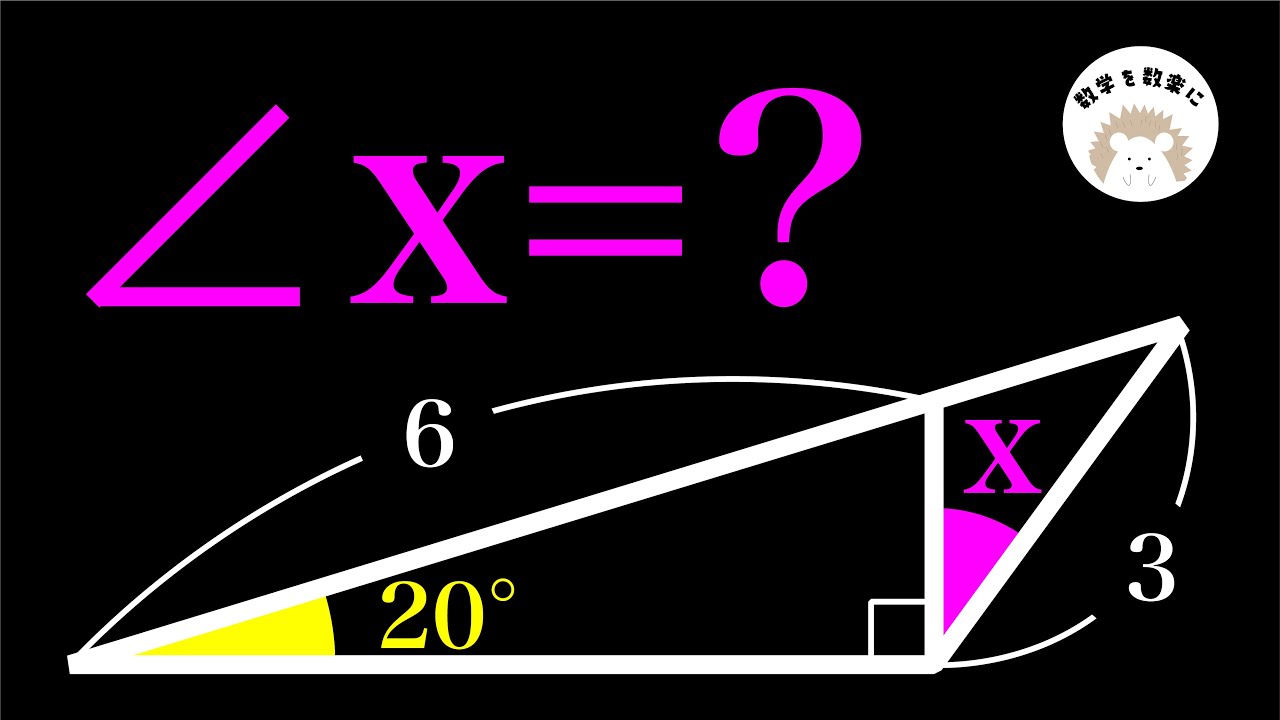
解が一個 2次方程式

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
xについての2次方程式
$x^2+5x+m+\frac{1}{4} = 0$の解が1コのときm=?
名古屋高等学校
この動画を見る
xについての2次方程式
$x^2+5x+m+\frac{1}{4} = 0$の解が1コのときm=?
名古屋高等学校
角度
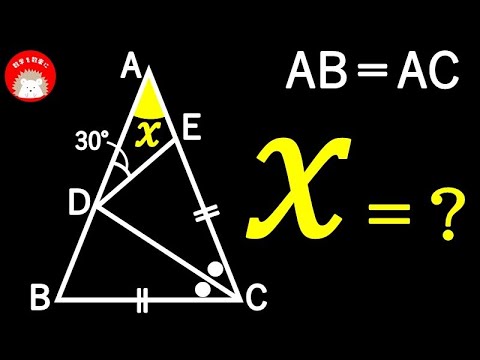
単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
AB=AC
$\angle x= ?$
*図は動画内参照
この動画を見る
AB=AC
$\angle x= ?$
*図は動画内参照
穴埋め問題
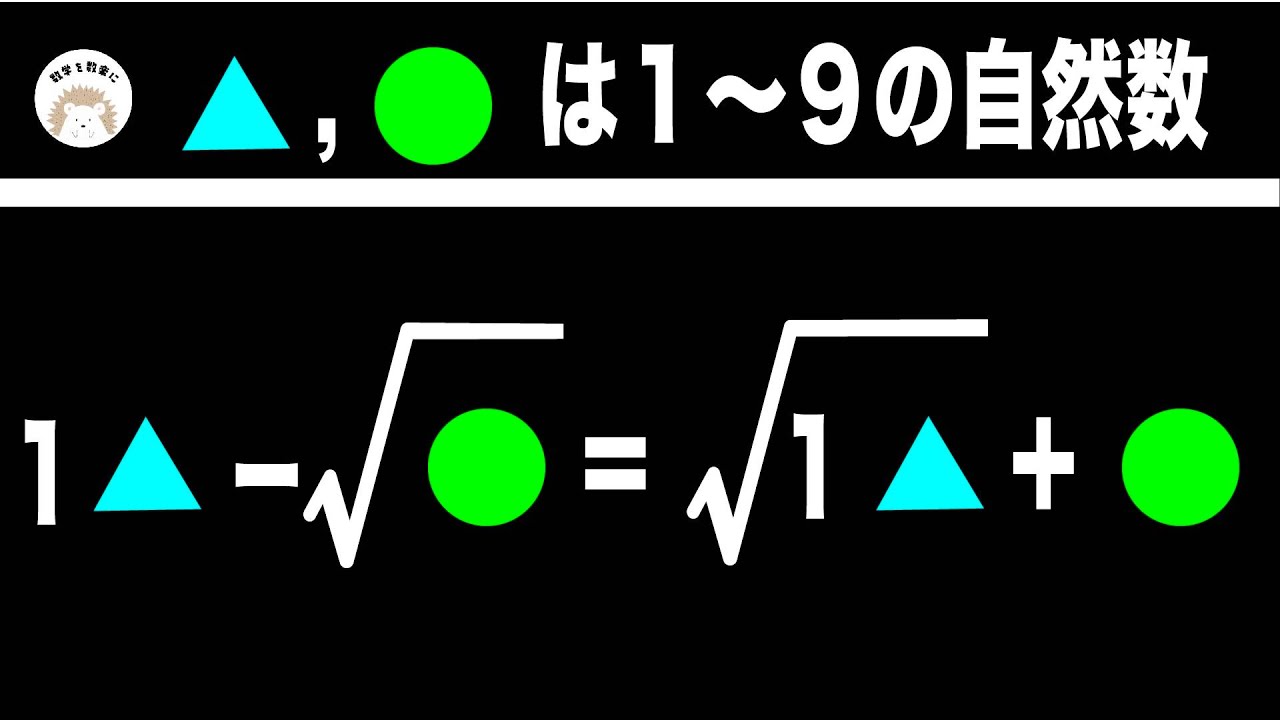
単元:
#数学(中学生)#中3数学#平方根
指導講師:
数学を数楽に
問題文全文(内容文):
$\boxed x$ , $\boxed y$は1~9の自然数
$1\boxed x - \sqrt{\boxed y} = \sqrt{1\boxed x} + \boxed y$
この動画を見る
$\boxed x$ , $\boxed y$は1~9の自然数
$1\boxed x - \sqrt{\boxed y} = \sqrt{1\boxed x} + \boxed y$
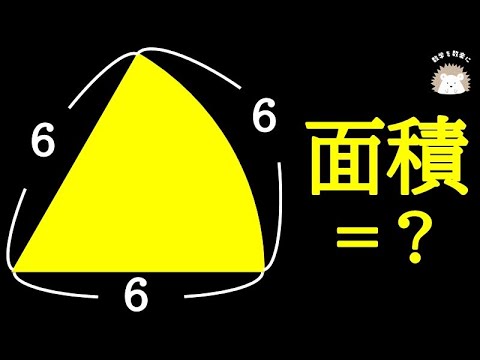
πが消えることを何て言う? おうぎ形の面積
2次方程式 解き方3通り 四天王寺高校

因数分解 東大寺学園

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$(a+1)^4-(4a^2+1)(a+1)^2+4a^2$を因数分解
東大寺学園高等学校
この動画を見る
$(a+1)^4-(4a^2+1)(a+1)^2+4a^2$を因数分解
東大寺学園高等学校
中学生の解き方 高校生の解き方
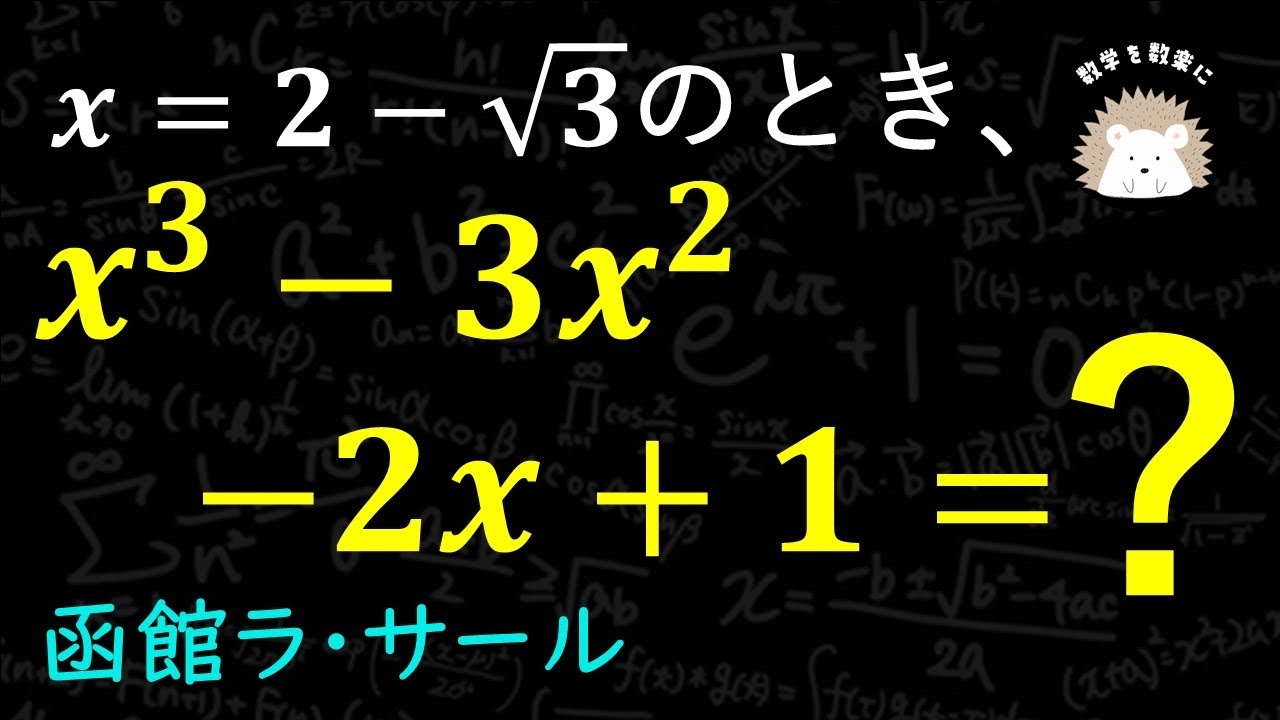
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x=2-\sqrt 3$のとき
$x^3-3x^2-2x+1$
函館ラ・サール高等学校
この動画を見る
$x=2-\sqrt 3$のとき
$x^3-3x^2-2x+1$
函館ラ・サール高等学校
平方根 式の値 早稲田実業

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x=\frac{6-\sqrt{28}}{4}$のとき
$8x^2-24x-5$
早稲田実業学校
この動画を見る
$x=\frac{6-\sqrt{28}}{4}$のとき
$8x^2-24x-5$
早稲田実業学校
角度 解けたら楽しい レベルC
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
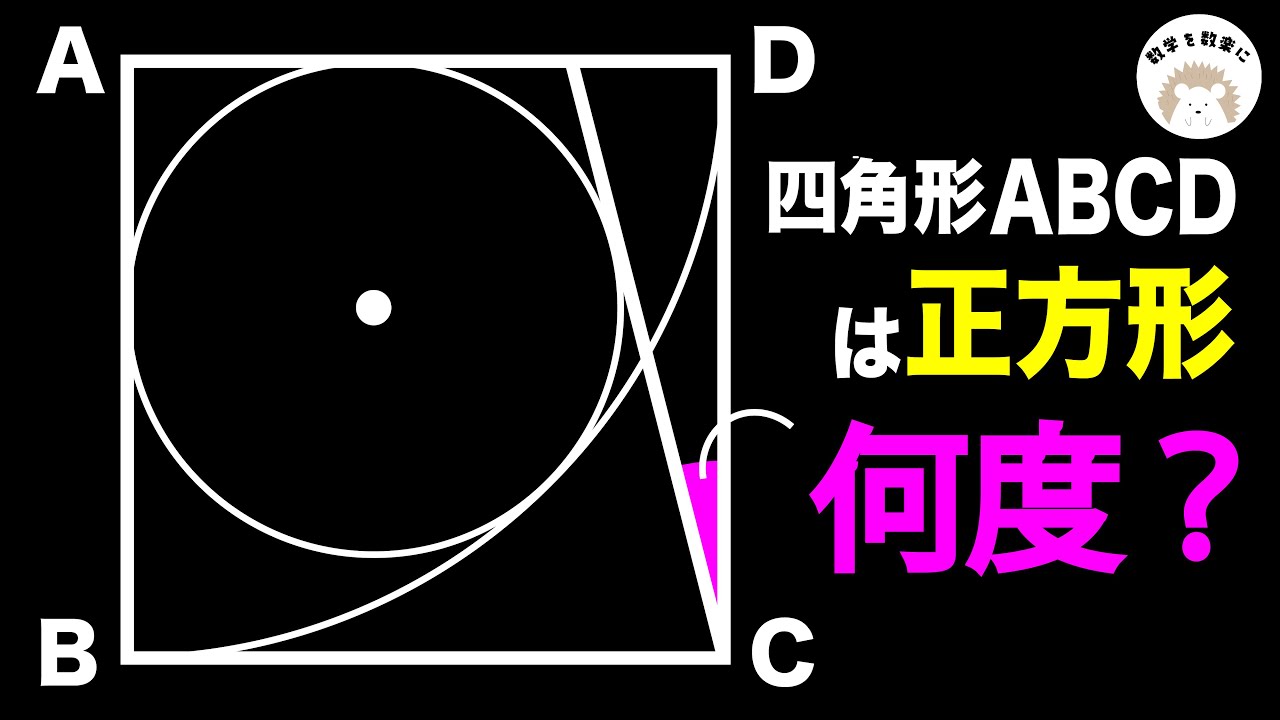
四角形ABCDは正方形
$\angle x=?$
*図は動画内参照
この動画を見る
四角形ABCDは正方形
$\angle x=?$
*図は動画内参照
平方根

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt 3= a$とするとき
$\sqrt{12}$をaで表せ
海星高等学校
この動画を見る
$\sqrt 3= a$とするとき
$\sqrt{12}$をaで表せ
海星高等学校
高校受験 数学 因数分解

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$abc(abc-2c)-3c^2$を因数分解
城西大学付属川越高等学校
この動画を見る
$abc(abc-2c)-3c^2$を因数分解
城西大学付属川越高等学校
□にあてはめる
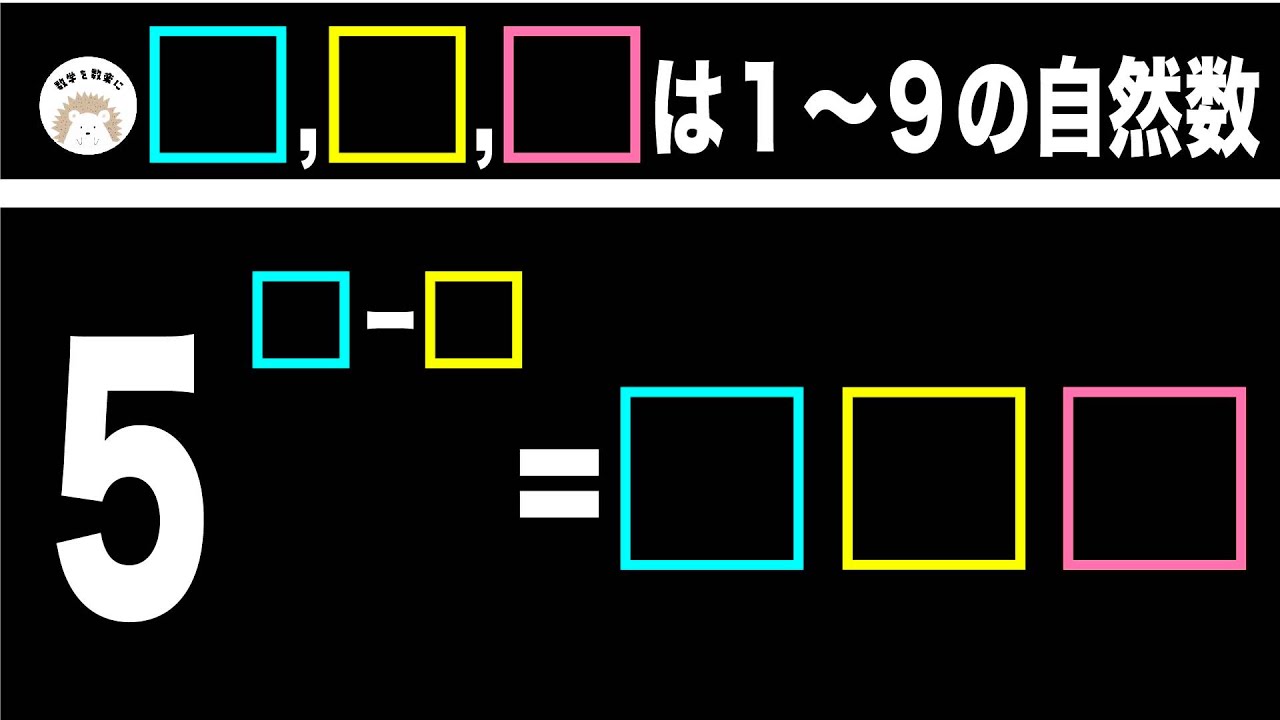
単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
数学を数楽に
問題文全文(内容文):
$5^{\fbox{x} - \fbox{y}} =\fbox{x} \fbox{y} \fbox{z} $
$\fbox{x} \fbox{y} \fbox{z} $(1~9の自然数)
この動画を見る
$5^{\fbox{x} - \fbox{y}} =\fbox{x} \fbox{y} \fbox{z} $
$\fbox{x} \fbox{y} \fbox{z} $(1~9の自然数)
大学入試の因数分解

単元:
#数Ⅰ#数Ⅱ#数と式#複素数と方程式#式の計算(整式・展開・因数分解)#複素数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
整数、実数、複素数の各範囲で因数分解せよ。
$x^4-x^2-2=$
この動画を見る
整数、実数、複素数の各範囲で因数分解せよ。
$x^4-x^2-2=$
他の問題もあり!

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
x.y.zを整数とする。
次の条件を満たす整数の組(x,y,z)は全部で何組か?
(1)$1 \leqq x \leqq 5$ , $1 \leqq y \leqq 5$ , $1 \leqq z \leqq 5$
(2)$1 \leqq x \lt y \lt z \leqq 5$
(3)$x+y+z = 5$ $ \quad x \geqq 1 ,y \geqq 1,z \geqq 1$
(4)$x+y+z = 5$ $ \quad x \geqq 0 ,y \geqq 0,z \geqq 0$
(5)$1 \leqq x \leqq y \leqq z \leqq 5$
大阪経済大学
この動画を見る
x.y.zを整数とする。
次の条件を満たす整数の組(x,y,z)は全部で何組か?
(1)$1 \leqq x \leqq 5$ , $1 \leqq y \leqq 5$ , $1 \leqq z \leqq 5$
(2)$1 \leqq x \lt y \lt z \leqq 5$
(3)$x+y+z = 5$ $ \quad x \geqq 1 ,y \geqq 1,z \geqq 1$
(4)$x+y+z = 5$ $ \quad x \geqq 0 ,y \geqq 0,z \geqq 0$
(5)$1 \leqq x \leqq y \leqq z \leqq 5$
大阪経済大学





