 東邦大学付属東邦中学
東邦大学付属東邦中学
 東邦大学付属東邦中学
東邦大学付属東邦中学
2024年東邦大付属東邦中算数「相似」中学受験指導歴20年のプロ解説

単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#相似と相似を利用した問題#東邦大学付属東邦中学
指導講師:
重吉
問題文全文(内容文):
動画内の図のような、三角形$ABC$があります。
このとき、$AD$の長さは何cmか求めなさい。
ただし、同じしるしはそれぞれ同じ角度を表しています。
出典:東邦大学付属東邦中学校 入試問題
この動画を見る
動画内の図のような、三角形$ABC$があります。
このとき、$AD$の長さは何cmか求めなさい。
ただし、同じしるしはそれぞれ同じ角度を表しています。
出典:東邦大学付属東邦中学校 入試問題
2023年東邦大付属東邦中学校算数「旅人算」

単元:
#算数(中学受験)#過去問解説(学校別)#速さ#旅人算・通過算・流水算#東邦大学付属東邦中学
指導講師:
重吉
問題文全文(内容文):
2023年東邦大付属東邦中学校算数「旅人算」
スタート地点Oを出発してAとCが____分後に出会う場所をP、Bがいる場所をQ、その____分____秒後にBとCが出会う場所をRとする。
PQ間の距離 = OP-OQ
= Aが____分間で進んだ距離で進んだ距離 - Bが____分間で進んだ距離
=____ m/分 $\times$ ____分 - ____ m/分 $\times$ ____分
=(____ - ____) $\times$ ____ = ____ $\times$ ____ = ____m
動画内の図より、BCは____分____秒後にR地点で出会う。
(1)Cさんの速さを求めよ。
(2)池1周が何mか求めよ。
この動画を見る
2023年東邦大付属東邦中学校算数「旅人算」
スタート地点Oを出発してAとCが____分後に出会う場所をP、Bがいる場所をQ、その____分____秒後にBとCが出会う場所をRとする。
PQ間の距離 = OP-OQ
= Aが____分間で進んだ距離で進んだ距離 - Bが____分間で進んだ距離
=____ m/分 $\times$ ____分 - ____ m/分 $\times$ ____分
=(____ - ____) $\times$ ____ = ____ $\times$ ____ = ____m
動画内の図より、BCは____分____秒後にR地点で出会う。
(1)Cさんの速さを求めよ。
(2)池1周が何mか求めよ。
2023年東邦大学付属東邦中学校算数「相似、面積」

単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#相似と相似を利用した問題#東邦大学付属東邦中学
指導講師:
重吉
問題文全文(内容文):
2023年東邦大学付属東邦中学校算数「相似、面積」
長方形があり、影がついた部分の面積を求めよ。
※動画内の図を参照
この動画を見る
2023年東邦大学付属東邦中学校算数「相似、面積」
長方形があり、影がついた部分の面積を求めよ。
※動画内の図を参照
え!?これ小学生でも解けるの?2つ目の解き方が意外過ぎた!【中学受験算数】【東邦大東邦中】
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#東邦大学付属東邦中学
指導講師:
こばちゃん塾
問題文全文(内容文):
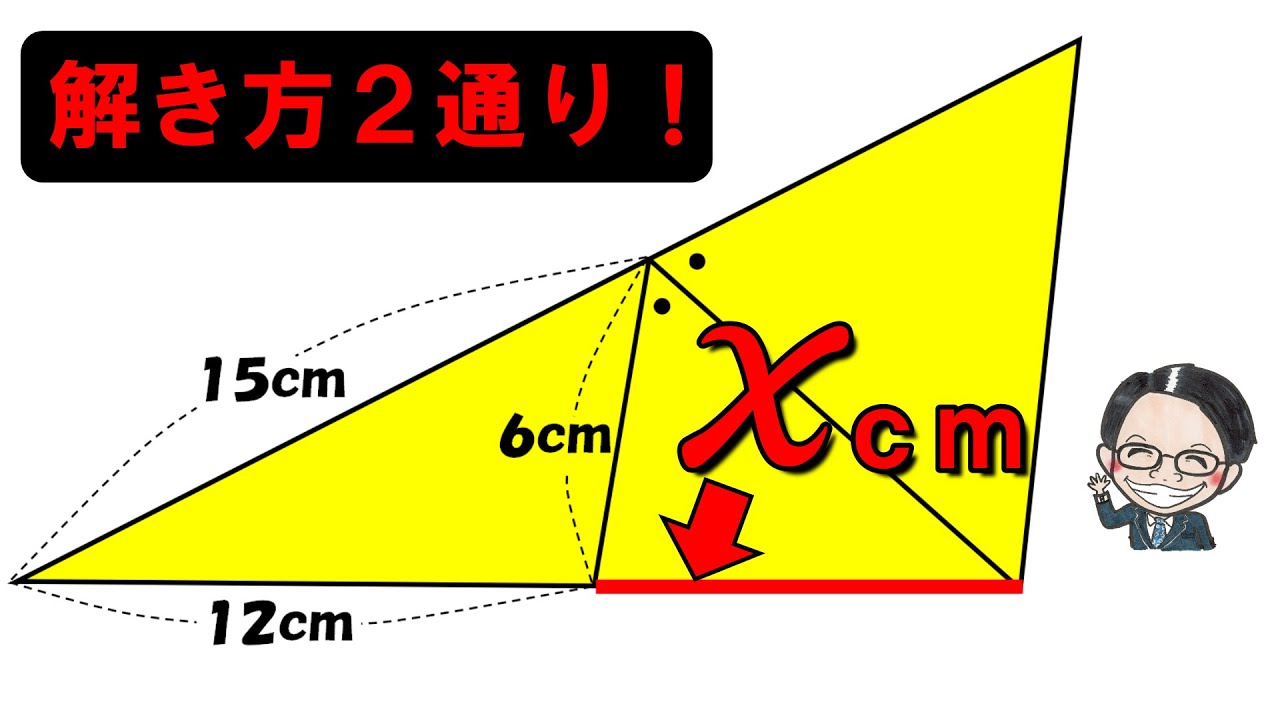
2022東邦大学付属東邦中学校
下図のECの長さは?
*図は動画内参照
この動画を見る
2022東邦大学付属東邦中学校
下図のECの長さは?
*図は動画内参照
この問題面白い!超便利なテクニックも紹介するよ!【中学受験算数】【東邦大学付属東邦中学校(改題)】
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#相似と相似を利用した問題#東邦大学付属東邦中学
指導講師:
こばちゃん塾
問題文全文(内容文):
・左図の長方形ABCDで、BO:ORは?
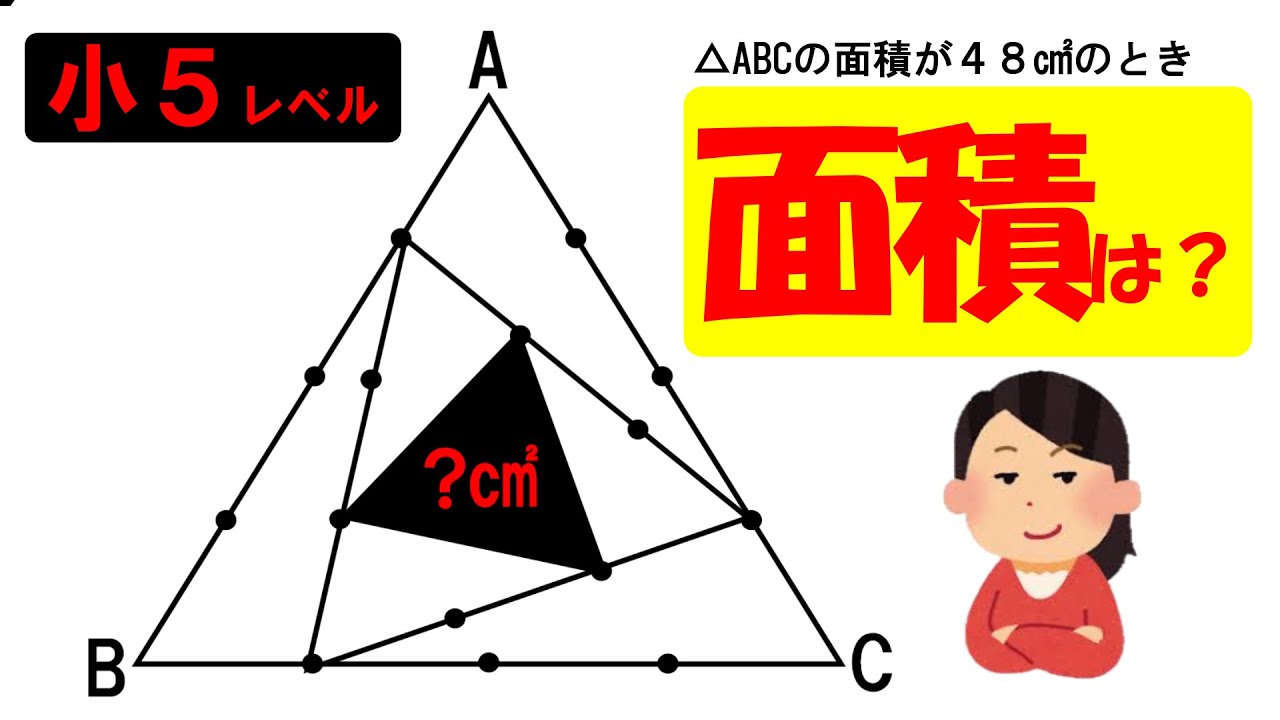
・三角形ABC,三角形DEF,三角形GHIは全て正三角形。
各辺上の点は,辺AB,BC,CAをそれぞれ4等分する点と,辺DE,EF,FDをそれぞれ3等分する点。
三角形ABCの面積が48㎠ のとき,三角形IGHの面積は?
*図は動画内参照
この動画を見る
・左図の長方形ABCDで、BO:ORは?
・三角形ABC,三角形DEF,三角形GHIは全て正三角形。
各辺上の点は,辺AB,BC,CAをそれぞれ4等分する点と,辺DE,EF,FDをそれぞれ3等分する点。
三角形ABCの面積が48㎠ のとき,三角形IGHの面積は?
*図は動画内参照
視聴者様のすご過ぎる解き方6選!視聴者の皆様から寄せられた秀逸な解き方、全て解説します!!【視聴者様参加型企画】
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#東邦大学付属東邦中学
指導講師:
こばちゃん塾
問題文全文(内容文):
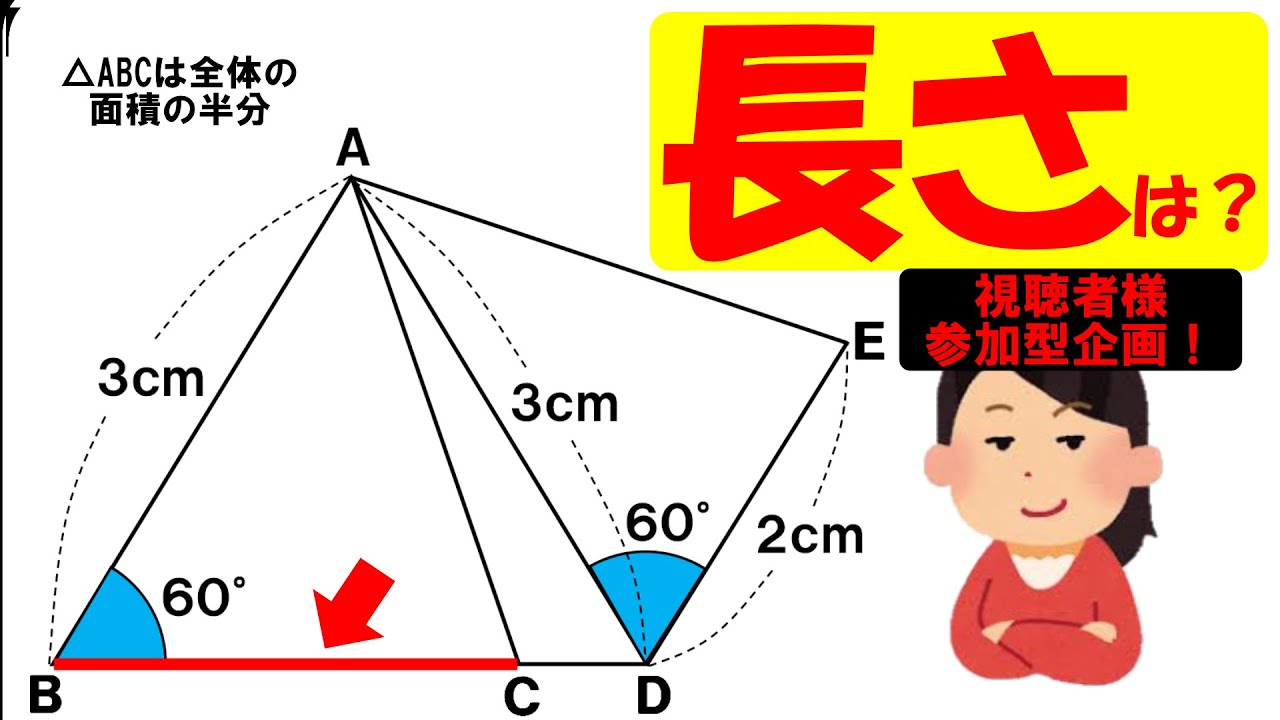
△ABC:四角形ABDE=1:2のとき、BCの長さは?
*図は動画内参照
この動画を見る
△ABC:四角形ABDE=1:2のとき、BCの長さは?
*図は動画内参照
私よりも良い解き方募集します!美しい解法が思いつきませんでした・・・。この問題、どう解く?【東邦大学付属東邦中学校】【2020】
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#東邦大学付属東邦中学
指導講師:
こばちゃん塾
問題文全文(内容文):
・左図の正六角形で、点Gは辺CDを3等分したうちの1つの点です。
正六角形の面積が1㎠のとき、三角形ACGの面積は?
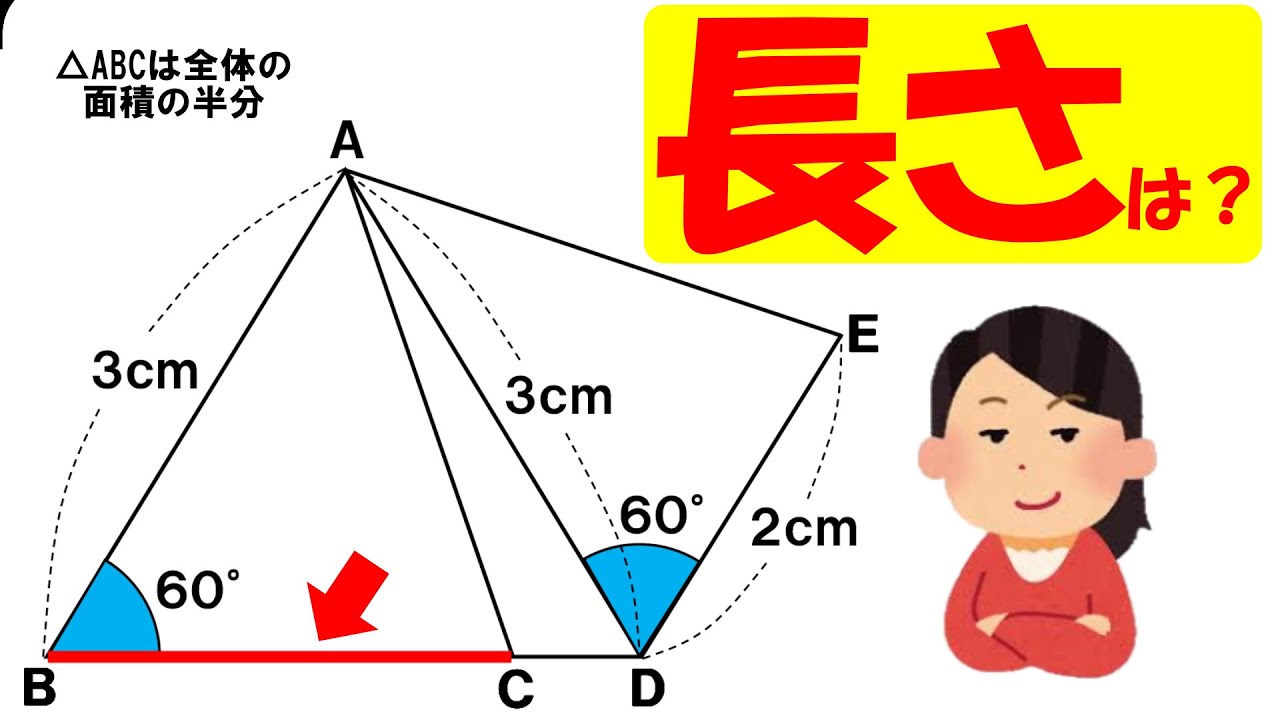
・左図において、三角形ABCの面積と四角形ABDEの面積比が1:2のとき、辺BCの長さは何㎝?
*図は動画内参照
この動画を見る
・左図の正六角形で、点Gは辺CDを3等分したうちの1つの点です。
正六角形の面積が1㎠のとき、三角形ACGの面積は?
・左図において、三角形ABCの面積と四角形ABDEの面積比が1:2のとき、辺BCの長さは何㎝?
*図は動画内参照
【第27問】東邦大学付属東邦中学2021年の入試問題【気付けばスッキリ!受験算数】

単元:
#過去問解説(学校別)#東邦大学付属東邦中学
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
$6468×2+939×5$を$13$で割ったあまりを求めよ
あまりの性質を利用しましょう.
東邦大学付属東邦中学2021年の入試問題
この動画を見る
$6468×2+939×5$を$13$で割ったあまりを求めよ
あまりの性質を利用しましょう.
東邦大学付属東邦中学2021年の入試問題
