 計算と数の性質
計算と数の性質
 計算と数の性質
計算と数の性質
計算速い人の頭はこんな感じ?
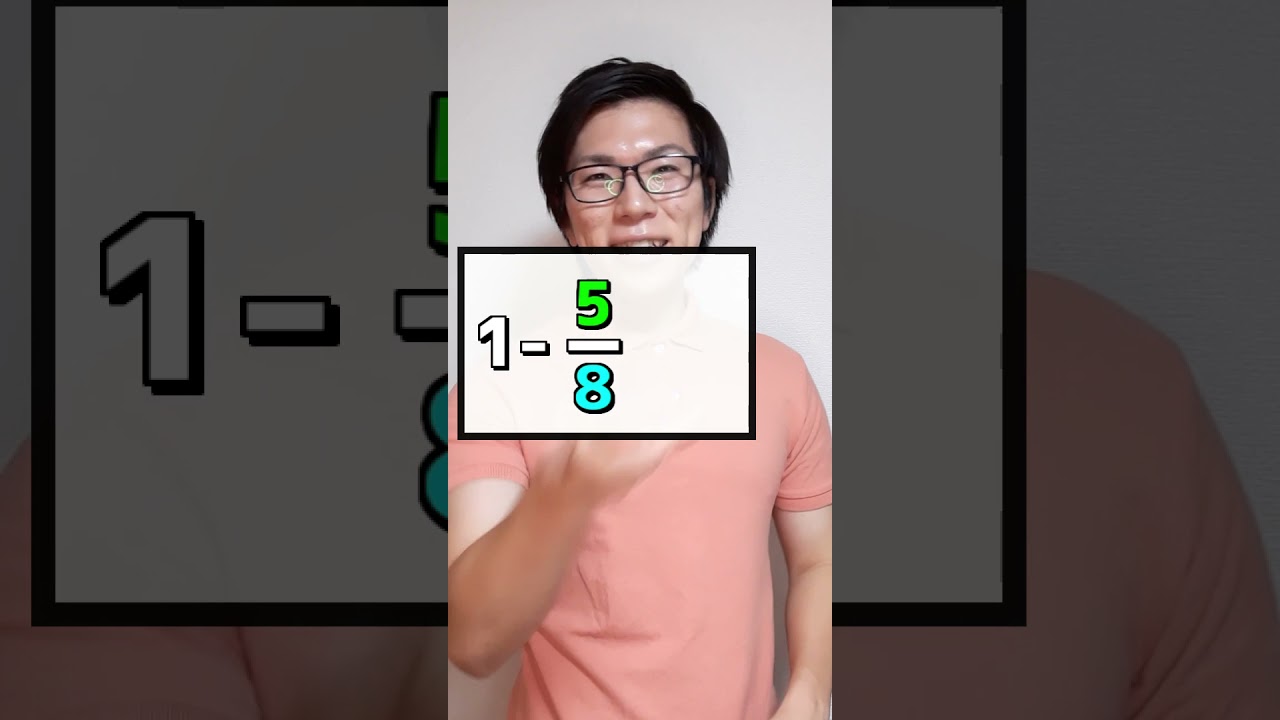
挑戦あれ!!

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
数学を数楽に
問題文全文(内容文):
$
\begin{array}{r}
▢▢▢ \\[-3pt]
\underline{\times\phantom{0}8▢}\\[-3pt]
▢▢▢▢ \\[-3pt]
\underline{\phantom{8}▢▢▢\phantom{00}} \\[-3pt]
▢▢▢▢
\end{array}
$
この動画を見る
$
\begin{array}{r}
▢▢▢ \\[-3pt]
\underline{\times\phantom{0}8▢}\\[-3pt]
▢▢▢▢ \\[-3pt]
\underline{\phantom{8}▢▢▢\phantom{00}} \\[-3pt]
▢▢▢▢
\end{array}
$
【裏技】単位変換

単元:
#算数(中学受験)#計算と数の性質#数学(中学生)#単位・比と割合・比例・反比例#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
単位変換の説明動画です
この動画を見る
単位変換の説明動画です
これ説明して

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#数学(中学生)#中1数学#中2数学#中3数学#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
2$\div \displaystyle \frac{1}{2}$
この動画を見る
2$\div \displaystyle \frac{1}{2}$
【裏技】これすげぇ

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#数学(中学生)#中1数学#中2数学#中3数学#約数・倍数を利用する問題#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
約分のテクニック紹介動画です
この動画を見る
約分のテクニック紹介動画です
【受験算数】規則性:1232112321…の20番目、34番目の数字を求めなさい。また、1~34番目までの和を求めなさい。

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#予習シ#予習シ算数・小4上#中学受験教材#規則性
指導講師:
理数個別チャンネル
問題文全文(内容文):
1232112321…の20番目、34番目の数字を求めなさい。また、1~34番目までの和を求めなさい。
この動画を見る
1232112321…の20番目、34番目の数字を求めなさい。また、1~34番目までの和を求めなさい。
【受験算数】規則性:ACBAACBAACBA…の30番目のアルファベットを求めなさい。

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#予習シ#予習シ算数・小4上#中学受験教材#規則性
指導講師:
理数個別チャンネル
問題文全文(内容文):
ACBAACBAACBA…の30番目のアルファベットを求めなさい。
この動画を見る
ACBAACBAACBA…の30番目のアルファベットを求めなさい。
約分の裏技・テクニック~意外と知らない~

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#数学(中学生)#中1数学#中2数学#中3数学#約数・倍数を利用する問題#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
2つの数字の公約数は、2つの数字の差の約数になる次の分数を約分せよ。
(1)$\displaystyle \frac{51}{68}$
(2)$\displaystyle \frac{10}{35}$
(3)$\displaystyle \frac{161}{115}$
(4)$\displaystyle \frac{5080}{5207}$
この動画を見る
2つの数字の公約数は、2つの数字の差の約数になる次の分数を約分せよ。
(1)$\displaystyle \frac{51}{68}$
(2)$\displaystyle \frac{10}{35}$
(3)$\displaystyle \frac{161}{115}$
(4)$\displaystyle \frac{5080}{5207}$
【受験算数】規則性:ABCABCABC…の30番目のアルファベットを求めなさい。

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#予習シ#予習シ算数・小4上#中学受験教材#規則性
指導講師:
理数個別チャンネル
問題文全文(内容文):
ABCABCABC…の30番目のアルファベットを求めなさい。
この動画を見る
ABCABCABC…の30番目のアルファベットを求めなさい。
【裏技】学校では教えてもらえない技

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#数学(中学生)#中1数学#中2数学#中3数学#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
8000のようなキリのいい数字に使えるひっ算の簡単計算方法紹介動画です
この動画を見る
8000のようなキリのいい数字に使えるひっ算の簡単計算方法紹介動画です
【裏技】×5の簡単な出し方

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#数学(中学生)#中1数学#中2数学#中3数学#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
×5の簡単な計算方法紹介動画です
この動画を見る
×5の簡単な計算方法紹介動画です
福田の数学〜上智大学2021年TEAP利用理系第1問(2)〜n進法

単元:
#計算と数の性質#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#規則性(周期算・方陣算・数列・日暦算・N進法)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(2)nを20以上の整数とする。n進法で表したとき、$n^3$の位の数が$1,n^2$の位の数が2,
$n^1$の位の数が$3,n^0$の位の数が0である数$1230_{(n)}$を$n+1$進法で表すと$(n+1)^2$の位
の数は$\boxed{\ \ あ\ \ }$であり、$(n+1)^1$の位の数は$\boxed{\ \ い\ \ }$であり、$(n+1)^0$の位の数は$\boxed{\ \ う\ \ }$である。
$\boxed{\ \ あ\ \ }\ ~\ \boxed{\ \ う\ \ }$の選択肢:
$(\textrm{a})0 (\textrm{b})1 (\textrm{c})2 (\textrm{d})3$
$(\textrm{e})n-2 (\textrm{f})n-3 (\textrm{g})n-1 (\textrm{g})n$
2021上智大学理系過去問
この動画を見る
${\Large\boxed{1}}$(2)nを20以上の整数とする。n進法で表したとき、$n^3$の位の数が$1,n^2$の位の数が2,
$n^1$の位の数が$3,n^0$の位の数が0である数$1230_{(n)}$を$n+1$進法で表すと$(n+1)^2$の位
の数は$\boxed{\ \ あ\ \ }$であり、$(n+1)^1$の位の数は$\boxed{\ \ い\ \ }$であり、$(n+1)^0$の位の数は$\boxed{\ \ う\ \ }$である。
$\boxed{\ \ あ\ \ }\ ~\ \boxed{\ \ う\ \ }$の選択肢:
$(\textrm{a})0 (\textrm{b})1 (\textrm{c})2 (\textrm{d})3$
$(\textrm{e})n-2 (\textrm{f})n-3 (\textrm{g})n-1 (\textrm{g})n$
2021上智大学理系過去問
【裏技】こんな×25の計算あり?

数理クイズ

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
指導講師:
鈴木貫太郎
問題文全文(内容文):
数理クイズを求めよ.$b=a+1$とする.
$2\times 2=4$
$3\times 3=1\boxed{a}$
$4\times 4=\boxed{a}\boxed{a}$
$5\times 5=\boxed{b}4$
$10 \times 10=100$
$11\times 11=121$
$12\times 12=144$
$13\times 13=\boxed{?}$
この動画を見る
数理クイズを求めよ.$b=a+1$とする.
$2\times 2=4$
$3\times 3=1\boxed{a}$
$4\times 4=\boxed{a}\boxed{a}$
$5\times 5=\boxed{b}4$
$10 \times 10=100$
$11\times 11=121$
$12\times 12=144$
$13\times 13=\boxed{?}$
数理クイズ

単元:
#計算と数の性質#いろいろな計算
指導講師:
鈴木貫太郎
問題文全文(内容文):
数理クイズ
$2\times 2=4$
$3\times 3=1\boxed{a}$
$4\times 4=\boxed{a}\boxed{a}$
$5\times 5=\boxed{b}4$
$b=a+1$
$10\times 10=100$
$11\times 11=121$
$12\times 12=144$
$13\times 13=\boxed{?}$
この動画を見る
数理クイズ
$2\times 2=4$
$3\times 3=1\boxed{a}$
$4\times 4=\boxed{a}\boxed{a}$
$5\times 5=\boxed{b}4$
$b=a+1$
$10\times 10=100$
$11\times 11=121$
$12\times 12=144$
$13\times 13=\boxed{?}$
4をかけるとひっくり返る4桁の数 浦和学院

単元:
#計算と数の性質#いろいろな計算#数学(中学生)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
\begin{array}{r}
ABCD \\[-3pt]
\underline{\times\phantom{00000}4}\\[-3pt]
DCBA \\[-3pt]
\end{array}
浦和学院高等学校
この動画を見る
\begin{array}{r}
ABCD \\[-3pt]
\underline{\times\phantom{00000}4}\\[-3pt]
DCBA \\[-3pt]
\end{array}
浦和学院高等学校
約数の個数が3個 専修大学松戸

単元:
#計算と数の性質#数学(中学生)#約数・倍数を利用する問題#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
1~50の自然数の中で約数が3コである数は全部で何コ?
専修大学松戸高等学校
この動画を見る
1~50の自然数の中で約数が3コである数は全部で何コ?
専修大学松戸高等学校
【裏技】5で終わる数の2乗の計算

9の引き算の新たな計算方法発見した

日大東北 筆算してもいいけど解けるかな?
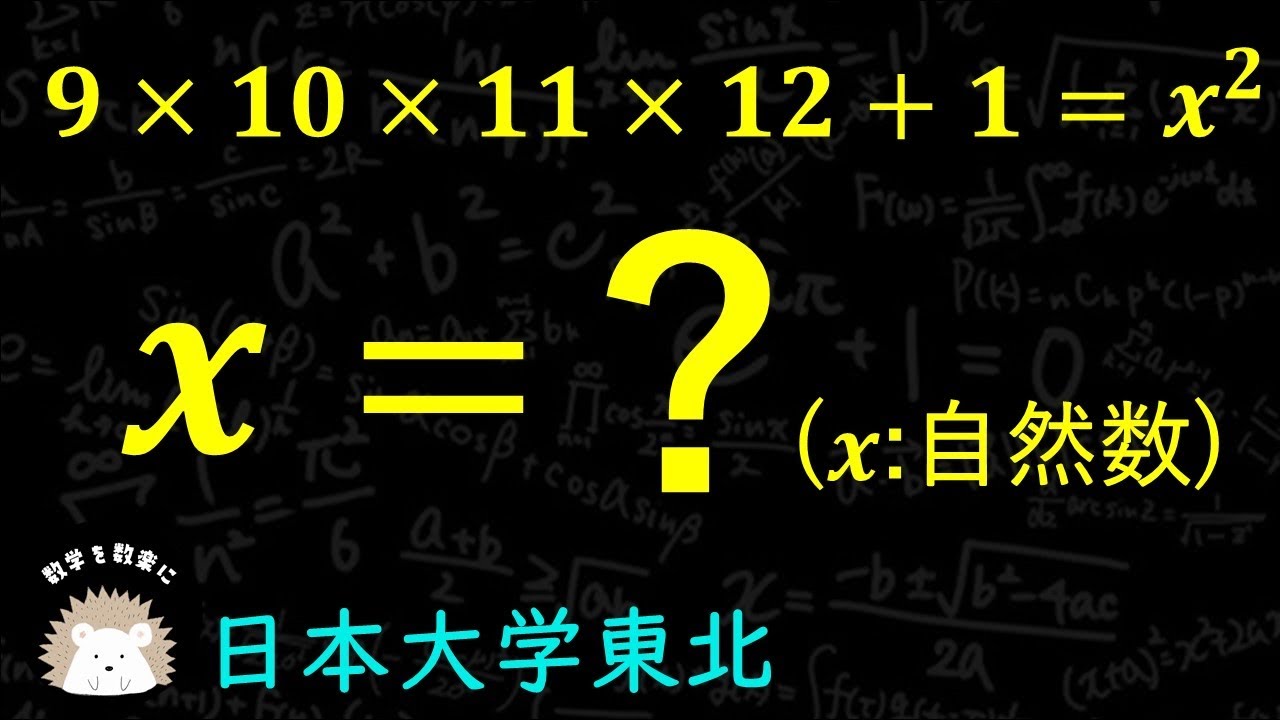
単元:
#計算と数の性質#いろいろな計算#数学(中学生)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$9×10×11×12+1 = x^2$(xは自然数)
日本大学東北高等学校
この動画を見る
$9×10×11×12+1 = x^2$(xは自然数)
日本大学東北高等学校
面白い数字集~完全数・友愛数・婚約数・ナルシシスト数~

単元:
#算数(中学受験)#計算と数の性質#数の性質その他#数学(中学生)#約数・倍数を利用する問題#規則性(周期算・方陣算・数列・日暦算・N進法)#その他#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
面白い数字集(完全数・友愛数・婚約数・ナルシシスト数)の紹介動画です
この動画を見る
面白い数字集(完全数・友愛数・婚約数・ナルシシスト数)の紹介動画です
最大公約数と最小公倍数の関係 東海大菅生 整数問題 知っていれば一瞬!!

単元:
#計算と数の性質#数学(中学生)#約数・倍数を利用する問題#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
aと12の
最小公倍数=180
最大公約数=6
a=?
東海大学菅生高等学校
この動画を見る
aと12の
最小公倍数=180
最大公約数=6
a=?
東海大学菅生高等学校
【裏技】×99の計算テクニック

【裏技】こんな計算方法あり?

1=0.999…になるんやけど?
中学入試 算数 中央大附属横浜

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)
指導講師:
数学を数楽に
問題文全文(内容文):
20.21×2020-202.1×▢=2021
中央大学附属横浜中学校
この動画を見る
20.21×2020-202.1×▢=2021
中央大学附属横浜中学校
中学入試 算数 覆面算 日大日吉中

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)
指導講師:
数学を数楽に
問題文全文(内容文):
\begin{array}{r}
A \\[-3pt]
AA \\[-3pt]
AAA \\[-3pt]
AAAA \\[-3pt]
AAAAA \\[-3pt]
AAAAAA \\[-3pt]
\underline{\times\phantom{0}AAAAAAA}\\[-3pt]
ABCABCD \\[-3pt]
\end{array}
日本大学中学校
この動画を見る
\begin{array}{r}
A \\[-3pt]
AA \\[-3pt]
AAA \\[-3pt]
AAAA \\[-3pt]
AAAAA \\[-3pt]
AAAAAA \\[-3pt]
\underline{\times\phantom{0}AAAAAAA}\\[-3pt]
ABCABCD \\[-3pt]
\end{array}
日本大学中学校
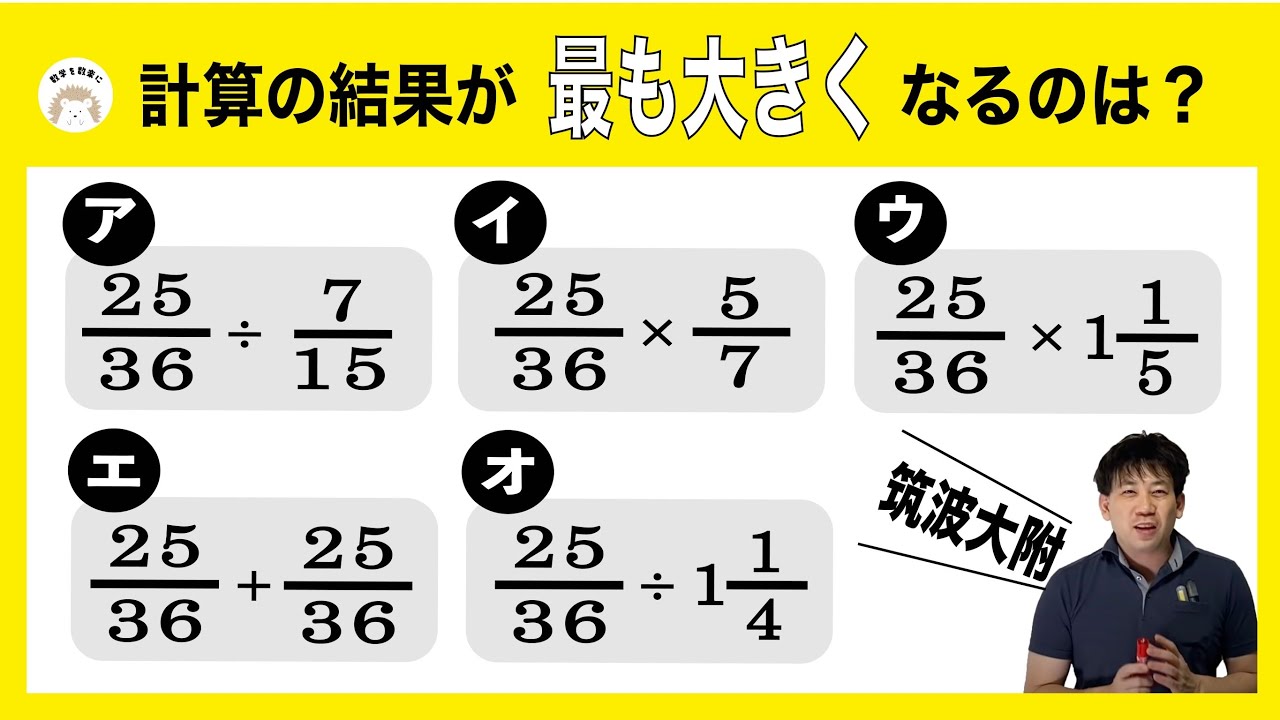
中学入試 算数 筑波大学附属中
単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)
指導講師:
数学を数楽に
問題文全文(内容文):
計算の結果が最も大きくなるのはどれ?
(ア) $\frac{25}{36} \div \frac{7}{15}$
(イ) $\frac{25}{36} \times \frac{5}{7}$
(ウ) $\frac{25}{36} \times 1\frac{1}{5}$
(エ) $\frac{25}{36} + \frac{25}{36}$
(オ) $\frac{25}{36} \div 1\frac{1}{4}$
筑波大学附属中学校
この動画を見る
計算の結果が最も大きくなるのはどれ?
(ア) $\frac{25}{36} \div \frac{7}{15}$
(イ) $\frac{25}{36} \times \frac{5}{7}$
(ウ) $\frac{25}{36} \times 1\frac{1}{5}$
(エ) $\frac{25}{36} + \frac{25}{36}$
(オ) $\frac{25}{36} \div 1\frac{1}{4}$
筑波大学附属中学校
数学 高校入試 3つの素数 日本女子大学附属高校

単元:
#計算と数の性質#数の性質その他#数学(中学生)#約数・倍数を利用する問題#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
条件を満たす3つの素数は?
・3つの数の積は偶数
・3つの数の和は24
・どの2つの数の差も2以上
日本女子大学附属高等学校
この動画を見る
条件を満たす3つの素数は?
・3つの数の積は偶数
・3つの数の和は24
・どの2つの数の差も2以上
日本女子大学附属高等学校
【中学数学】規則性の裏技~n番目を一瞬で求めます~
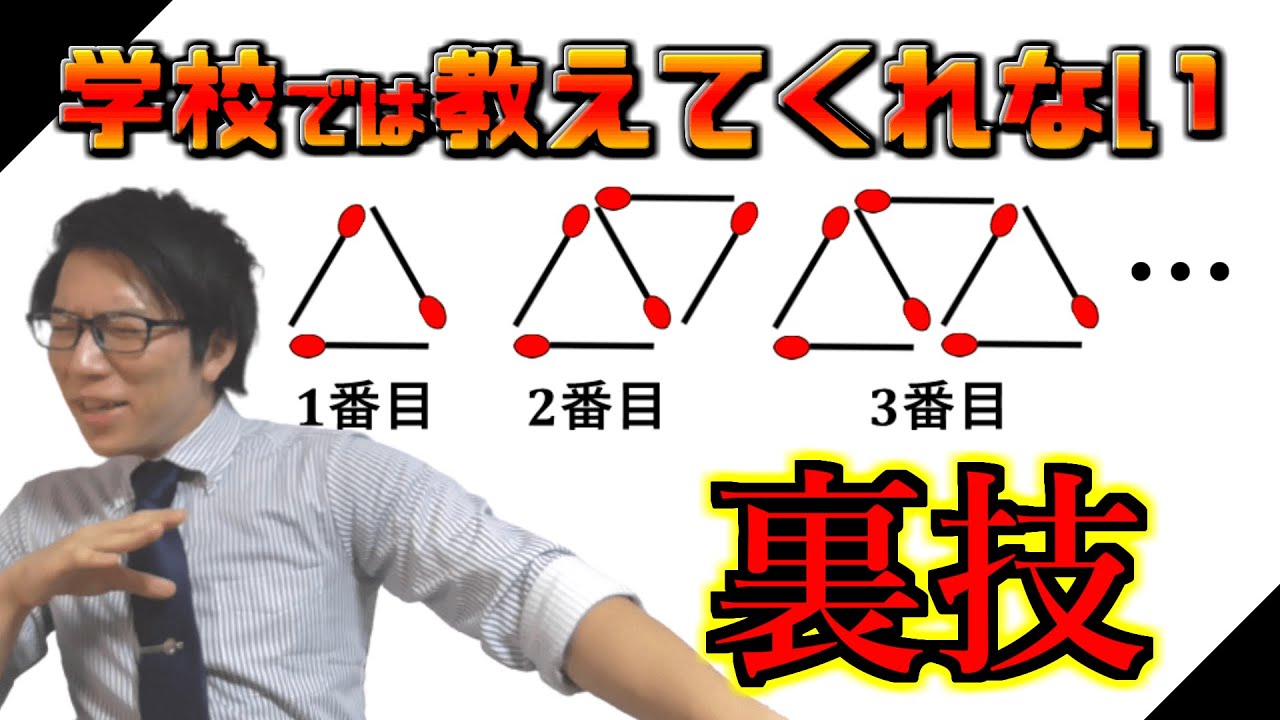
単元:
#算数(中学受験)#計算と数の性質#数学(中学生)#中1数学#中2数学#中3数学#規則性(周期算・方陣算・数列・日暦算・N進法)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
【中学数学】規則性の裏技紹介動画です
この動画を見る
【中学数学】規則性の裏技紹介動画です
