計算と数の性質
計算と数の性質
【中学受験算数】【分配算】ゼロから始める中学受験算数１１ わかる！和差算・分配算！
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師：
こばちゃん塾
問題文全文(内容文)：
1⃣和が52、差が16である2つの整数を求めよ。
2⃣和が116差が18である2つの整数を求めよ。
3⃣A,B,C3つの数があり、その和は378です。
BはAより2大きく、CはBより5大きいとき、Aはいくつですか。
4⃣60個のおはじきを姉と妹で分けたら、姉の個数は妹の個数の3倍よりも4個多くなりました。姉の個数は何個ですか。
5⃣90枚のカードを兄と弟で分けたら、兄の枚数は弟の枚数の2倍よりも6枚多くなりました。2人のカードはそれぞれ何枚ですか。
この動画を見る
1⃣和が52、差が16である2つの整数を求めよ。
2⃣和が116差が18である2つの整数を求めよ。
3⃣A,B,C3つの数があり、その和は378です。
BはAより2大きく、CはBより5大きいとき、Aはいくつですか。
4⃣60個のおはじきを姉と妹で分けたら、姉の個数は妹の個数の3倍よりも4個多くなりました。姉の個数は何個ですか。
5⃣90枚のカードを兄と弟で分けたら、兄の枚数は弟の枚数の2倍よりも6枚多くなりました。2人のカードはそれぞれ何枚ですか。
【中学受験算数】【数列】ゼロから始める中学受験算数１０ 数列を徹底攻略！！！
単元：
#算数(中学受験)#計算と数の性質#規則性（周期算・方陣算・数列・日暦算・N進法）
指導講師：
こばちゃん塾
問題文全文(内容文)：
1⃣次の数列の$\boxed ア$、$\boxed イ$にあてはまる数を答えましょう。
(1)2,4,6,$\boxed ア$,10,12,$\boxed イ$,16・・・
(2)1,2,4,7,11,16,$\boxed ア$,$\boxed イ$,37・・・
(3)1,4,9,$\boxed ア$,25,36,$\boxed イ$,64,81・・・
(4)1,1,2,3,5,8,$\boxed ア$,21,$\boxed イ$,55・・・
2⃣次の数列の$\boxed ア$,$\boxed イ$にあてはまる数を答えましょう。
(1)1,8,27,$\boxed ア$,125,216,$\boxed イ$,512・・・
(2)6,7,13,20,$\boxed ア$,53,86,$\boxed イ$,225・・・
3⃣4,7,10,13,16,19,22,25・・・という数列で
(1)|5|は左から何番目ですか。
(2)はじめから30番目までの和はいくつですか。
4⃣1,5,9,13,17,21,25,29・・・という数列で
(1)左から25番目の数はいくつですか。
(2)149は左から何番目の数ですか。
(3)はじめの数から100番目の数までの和を求めましょう。
この動画を見る
1⃣次の数列の$\boxed ア$、$\boxed イ$にあてはまる数を答えましょう。
(1)2,4,6,$\boxed ア$,10,12,$\boxed イ$,16・・・
(2)1,2,4,7,11,16,$\boxed ア$,$\boxed イ$,37・・・
(3)1,4,9,$\boxed ア$,25,36,$\boxed イ$,64,81・・・
(4)1,1,2,3,5,8,$\boxed ア$,21,$\boxed イ$,55・・・
2⃣次の数列の$\boxed ア$,$\boxed イ$にあてはまる数を答えましょう。
(1)1,8,27,$\boxed ア$,125,216,$\boxed イ$,512・・・
(2)6,7,13,20,$\boxed ア$,53,86,$\boxed イ$,225・・・
3⃣4,7,10,13,16,19,22,25・・・という数列で
(1)|5|は左から何番目ですか。
(2)はじめから30番目までの和はいくつですか。
4⃣1,5,9,13,17,21,25,29・・・という数列で
(1)左から25番目の数はいくつですか。
(2)149は左から何番目の数ですか。
(3)はじめの数から100番目の数までの和を求めましょう。
【中学受験算数】【分数】ゼロから始める中学受験算数９ 小数と分数の問題はこれだけでOK！！
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師：
こばちゃん塾
問題文全文(内容文)：
1⃣$\frac{3}{7},0.45,\frac{4}{9},\frac{2}{5}$を小さいほうから順に並べましょう。
2⃣$\frac{7}{9},0.78,\frac{11}{15},\frac{5}{7},\frac{8}{11}$を小さいほうから順に並べましょう。
3⃣$\frac{3}{10}$と$\frac{5}{12}$の間にあり、分母が5である分数を求めましょう。
4⃣$\frac{3}{4}$と$\frac{8}{9}$の間にあり、分母が6である分数を求めましょう。
5⃣分母と分子の和が102で約分すると$\frac{2}{15}$になる分数を求めましょう。
6⃣分母と分子の和が238で約分すると$\frac{3}{11}$になる分数を求めましょう。
この動画を見る
1⃣$\frac{3}{7},0.45,\frac{4}{9},\frac{2}{5}$を小さいほうから順に並べましょう。
2⃣$\frac{7}{9},0.78,\frac{11}{15},\frac{5}{7},\frac{8}{11}$を小さいほうから順に並べましょう。
3⃣$\frac{3}{10}$と$\frac{5}{12}$の間にあり、分母が5である分数を求めましょう。
4⃣$\frac{3}{4}$と$\frac{8}{9}$の間にあり、分母が6である分数を求めましょう。
5⃣分母と分子の和が102で約分すると$\frac{2}{15}$になる分数を求めましょう。
6⃣分母と分子の和が238で約分すると$\frac{3}{11}$になる分数を求めましょう。
【中学受験算数】【整数】ゼロから始める中学受験算数８ ややこしさを瞬殺！整数の問題を攻略せよ！！（上級問題）
単元：
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題
指導講師：
こばちゃん塾
問題文全文(内容文)：
1⃣18と34のどちらをわっても2あまる整数をすべて求めましょう。
2⃣118と82のどちらをわっても10あまる整数をすべて求めましょう。
3⃣7でわっても4でわっても3あまる整数のうち、100にいちばん近い数を求めよ。
4⃣4でわっても6でわっても1あまる整数のうち、100にいちばん近い数を求めよ。
5⃣○○○○○は0、○○○○●は1、○○○●○は2、○○○●●は3、○○●○○は4、
○○●○●は5、○●○○○は8、○●○●○は10
(1)●○●○●はいくつ？
(2)30を5つの○に色をぬって表しましょう。
6⃣○○○○○は0、△○○○○は1、○△○○○は2、○○△○○は4、△○○△○は9、
○○△○△は20
(1)○△△△○はいくつ？
(2)27を○と△を5個すべて表しましょう。
この動画を見る
1⃣18と34のどちらをわっても2あまる整数をすべて求めましょう。
2⃣118と82のどちらをわっても10あまる整数をすべて求めましょう。
3⃣7でわっても4でわっても3あまる整数のうち、100にいちばん近い数を求めよ。
4⃣4でわっても6でわっても1あまる整数のうち、100にいちばん近い数を求めよ。
5⃣○○○○○は0、○○○○●は1、○○○●○は2、○○○●●は3、○○●○○は4、
○○●○●は5、○●○○○は8、○●○●○は10
(1)●○●○●はいくつ？
(2)30を5つの○に色をぬって表しましょう。
6⃣○○○○○は0、△○○○○は1、○△○○○は2、○○△○○は4、△○○△○は9、
○○△○△は20
(1)○△△△○はいくつ？
(2)27を○と△を5個すべて表しましょう。
【受験算数】小数・分数：分数を分子1の足し算に分ける問題
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$\dfrac{3}{5}=\dfrac{1}{ア}+\dfrac{1}{イ}$のときア、イに当てはまる整数を求めなさ。ただし、$ア\ltイ$する。
この動画を見る
$\dfrac{3}{5}=\dfrac{1}{ア}+\dfrac{1}{イ}$のときア、イに当てはまる整数を求めなさ。ただし、$ア\ltイ$する。
中学入試問題 駒場東邦 整数問題
単元：
#算数(中学受験)#計算と数の性質#数の性質その他#過去問解説(学校別)#駒場東邦中学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$121 \times 122 \times 123 \times 124 \times 125 \times 126 \times 127 \times$
$ 128 \times 129 \times 130$
1の位から順にみて最初に現れる0以外の数字は？
出典：駒場東邦中学校 過去問
この動画を見る
$121 \times 122 \times 123 \times 124 \times 125 \times 126 \times 127 \times$
$ 128 \times 129 \times 130$
1の位から順にみて最初に現れる0以外の数字は？
出典：駒場東邦中学校 過去問
【受験算数】循環小数(応用)：0.481818181…の分数を小数で表すには！？
単元：
#算数(中学受験)#計算と数の性質#規則性（周期算・方陣算・数列・日暦算・N進法）
教材：
#SPX#6年算数W-支援#中学受験教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の小数を分数で表しなさい。(3)$0.481818181…$
但し、$\dfrac{1}{9}=0.1111…、\dfrac{1}{99}=0.010101…、\dfrac{1}{999}=0.001001001…$を利用する
この動画を見る
次の小数を分数で表しなさい。(3)$0.481818181…$
但し、$\dfrac{1}{9}=0.1111…、\dfrac{1}{99}=0.010101…、\dfrac{1}{999}=0.001001001…$を利用する
【受験算数】数の性質：1×2×3×4×...×100 この数3で何回割れるでしょう？
単元：
#算数(中学受験)#計算と数の性質#数の性質その他
指導講師：
理数個別チャンネル
問題文全文(内容文)：
①1~100まで掛け算した答えを3で割っていくと何回割ることができるか
②1~50まで掛け算した答えには０が何個並ぶのか
この動画を見る
①1~100まで掛け算した答えを3で割っていくと何回割ることができるか
②1~50まで掛け算した答えには０が何個並ぶのか
リクエスト頂いた規則性やっていきましょう【中学受験】
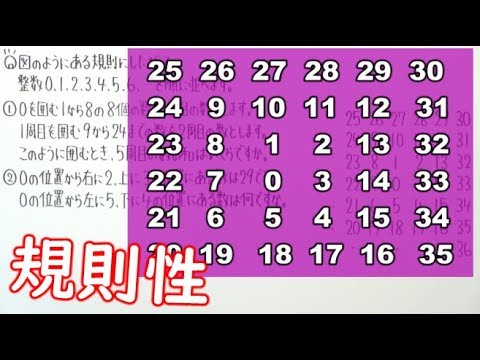
単元：
#算数(中学受験)#計算と数の性質#規則性（周期算・方陣算・数列・日暦算・N進法）
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
図のようにある規則にしたがって、整数0.1.2.3.4.5.6...を順に並べます。
①
0を囲む1から8の8個の数を1周目の数とします。
1周目を囲む9から24までの数を2周目の数とします。
このように囲むとき、5周目の数の和はいくらですか。
②
0の位置から右に2、上に3の位置にある数は29です。
0の位置から左に5、下に4の位置にある数は何ですか。
この動画を見る
図のようにある規則にしたがって、整数0.1.2.3.4.5.6...を順に並べます。
①
0を囲む1から8の8個の数を1周目の数とします。
1周目を囲む9から24までの数を2周目の数とします。
このように囲むとき、5周目の数の和はいくらですか。
②
0の位置から右に2、上に3の位置にある数は29です。
0の位置から左に5、下に4の位置にある数は何ですか。
中学入試の問題をやってみます【お試し】
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$12×(\frac{1}{2}-\frac{1}{3})-(\frac{1}{2}\div 0.75-\frac{4}{9})×9$
②$93-89+83-71+59-53+50-47+41-29+17-11+7$
③$(954-459-25×16+0.4)\div(\frac{1}{12}+\frac{1}{84}+\frac{1}{210}) $
④$(0.375×24+2.5×0.625×16)×19-25×12-125×16-1.4×190$
⑤$1×1×1+3+5+3×3×3+13+15+17+19+5×5×5+31+33+35+37+39+41$
この動画を見る
①$12×(\frac{1}{2}-\frac{1}{3})-(\frac{1}{2}\div 0.75-\frac{4}{9})×9$
②$93-89+83-71+59-53+50-47+41-29+17-11+7$
③$(954-459-25×16+0.4)\div(\frac{1}{12}+\frac{1}{84}+\frac{1}{210}) $
④$(0.375×24+2.5×0.625×16)×19-25×12-125×16-1.4×190$
⑤$1×1×1+3+5+3×3×3+13+15+17+19+5×5×5+31+33+35+37+39+41$
【数学】分数分の分数～意外と知らないテクニック～
灘中 整数問題
単元：
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題#過去問解説(学校別)#灘中学校
指導講師：
鈴木貫太郎
問題文全文(内容文)：
灘中学校 過去問
次の999個の整数のうち、12の倍数は何個あるか？
1×1998、2×1997、3×1996・・・999×1000
この動画を見る
灘中学校 過去問
次の999個の整数のうち、12の倍数は何個あるか？
1×1998、2×1997、3×1996・・・999×1000
名古屋市立（医） Mathematics Japanese university entrance exam
単元：
#計算と数の性質#数の性質その他#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋市立大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
'08名古屋市立大学過去問題
$99^{100}$と$100^{99}$
大小比較
この動画を見る
'08名古屋市立大学過去問題
$99^{100}$と$100^{99}$
大小比較
西暦3200年は閏年か？超無駄な雑学
灘中 整数問題
単元：
#算数(中学受験)#計算と数の性質#数の性質その他#過去問解説(学校別)#灘中学校
指導講師：
鈴木貫太郎
問題文全文(内容文)：
灘中学校過去問題
連続する4つの数(0,1,2,3),(1,2,3,4)~(6,7,8,9)から3つの数を選んで3桁の数を作る。その3桁の数と残りの数を3で割ったときの余りが同じになるものは全部で何個か。
この動画を見る
灘中学校過去問題
連続する4つの数(0,1,2,3),(1,2,3,4)~(6,7,8,9)から3つの数を選んで3桁の数を作る。その3桁の数と残りの数を3で割ったときの余りが同じになるものは全部で何個か。
灘中 整数問題
単元：
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題#過去問解説(学校別)#灘中学校
指導講師：
鈴木貫太郎
問題文全文(内容文)：
灘中学校過去問題
15÷4=3.75 , 15÷125=0.12
のように15をある自然数で割るとき、ちょうど小数第2位を求めたところで割り算が終わる。
このような自然数の個数。
この動画を見る
灘中学校過去問題
15÷4=3.75 , 15÷125=0.12
のように15をある自然数で割るとき、ちょうど小数第2位を求めたところで割り算が終わる。
このような自然数の個数。
灘中
単元：
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題#過去問解説(学校別)#灘中学校
指導講師：
鈴木貫太郎
問題文全文(内容文)：
灘中学校過去問題
6桁の整数ABCDEFの一番上の位のAを一の位に移した数BCDEFAがもとの数の3倍になるのは2つある。大きい方をxとする
x=▢ $\frac{x}{999999}$を約分
この動画を見る
灘中学校過去問題
6桁の整数ABCDEFの一番上の位のAを一の位に移した数BCDEFAがもとの数の3倍になるのは2つある。大きい方をxとする
x=▢ $\frac{x}{999999}$を約分
灘中 中学入試問題シリーズ 整数問題
単元：
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題#過去問解説(学校別)#灘中学校
指導講師：
鈴木貫太郎
問題文全文(内容文)：
灘中学校過去問題
6桁の整数 5ABC15が999の倍数である。
ABCを求めよ。
この動画を見る
灘中学校過去問題
6桁の整数 5ABC15が999の倍数である。
ABCを求めよ。
灘中 中学入試 整数問題
単元：
#算数(中学受験)#約数・倍数を利用する問題#過去問解説(学校別)#灘中学校
指導講師：
鈴木貫太郎
問題文全文(内容文)：
灘中学校過去問題
①4つの異なる数字
1,3,▢,9から異なる数字を取り出して並べる3桁の整数は24個でその平均は555
②5桁の36の倍数で2,3,5のどれもがいずれかの桁に現れる整数のうち最小のもの。
この動画を見る
灘中学校過去問題
①4つの異なる数字
1,3,▢,9から異なる数字を取り出して並べる3桁の整数は24個でその平均は555
②5桁の36の倍数で2,3,5のどれもがいずれかの桁に現れる整数のうち最小のもの。
灘中 中学入試にチャレンジ
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#灘中学校
指導講師：
鈴木貫太郎
問題文全文(内容文)：
灘中学校過去問題
$\quad$10桁 $\quad\quad$ 10桁
7777777777 7777777777
は計算すると20桁になる。この20桁の上10桁と下10桁の数の和を求めよ。
上2桁と下2桁の和とは1234なら12+34のこと
この動画を見る
灘中学校過去問題
$\quad$10桁 $\quad\quad$ 10桁
7777777777 7777777777
は計算すると20桁になる。この20桁の上10桁と下10桁の数の和を求めよ。
上2桁と下2桁の和とは1234なら12+34のこと
我が強いあなたの勉強法～「素直さ」と「ワガママさ」を両立させる方法～京大模試全国一位の勉強法【篠原好】
単元：
#計算と数の性質#その他#勉強法
指導講師：
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文)：
「素直さ」と「ワガママさ」を両立させる方法
「我が強い人の勉強法」についてお話しています。
この動画を見る
「素直さ」と「ワガママさ」を両立させる方法
「我が強い人の勉強法」についてお話しています。
【高校数学】 数B－７１ 複利計算
単元：
#計算と数の性質#いろいろな計算#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①毎年初めに$x$円ずつ積み立てて,5年間で10万円にするには,
何円ずつ貯金すればよいか求めよう.
ただし,年利率2%,1年ごとの複利で,$(1.02)^5=1.10$として計算し,
円未満は切り上げること.
②年利5%の1年ごとの複利で,毎年度の初めに20万円ずつ積み立てるとき,
元利合計は,7年度末にいくらになるか求めよう.
ただし,$(1.05)^7=1.4071$とし,1万円未満は切り捨てること.
この動画を見る
①毎年初めに$x$円ずつ積み立てて,5年間で10万円にするには,
何円ずつ貯金すればよいか求めよう.
ただし,年利率2%,1年ごとの複利で,$(1.02)^5=1.10$として計算し,
円未満は切り上げること.
②年利5%の1年ごとの複利で,毎年度の初めに20万円ずつ積み立てるとき,
元利合計は,7年度末にいくらになるか求めよう.
ただし,$(1.05)^7=1.4071$とし,1万円未満は切り捨てること.
【算数】小4-12 わり算の筆算②
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
【レベル３】
①
$\begin{array}{r}
\\[-3pt]
3\enclose{longdiv}{795\phantom{0}} \\[-3pt]
{\phantom{.0}} \\[-3pt]
\phantom{.} \\[-3pt]
{\phantom{.}} \\[-3pt]
\phantom{000}
\end{array}$
②
$\begin{array}{r}
\\[-3pt]
6\enclose{longdiv}{689\phantom{0}} \\[-3pt]
{\phantom{.0}} \\[-3pt]
\phantom{.} \\[-3pt]
{\phantom{.}} \\[-3pt]
\phantom{000}
\end{array}$
③
$\begin{array}{r}
\\[-3pt]
3\enclose{longdiv}{28\phantom{0}} \\[-3pt]
{\phantom{.0}} \\[-3pt]
\phantom{.} \\[-3pt]
{\phantom{.}} \\[-3pt]
\phantom{000}
\end{array}$
【レベル４】
④
$\begin{array}{r}
\\[-3pt]
6\enclose{longdiv}{312\phantom{0}} \\[-3pt]
{\phantom{.0}} \\[-3pt]
\phantom{.} \\[-3pt]
{\phantom{.}} \\[-3pt]
\phantom{000}
\end{array}$
⑤
$\begin{array}{r}
\\[-3pt]
4\enclose{longdiv}{53\phantom{0}} \\[-3pt]
{\phantom{.0}} \\[-3pt]
\phantom{.} \\[-3pt]
{\phantom{.}} \\[-3pt]
\phantom{000}
\end{array}$
⑥
$\begin{array}{r}
\\[-3pt]
3\enclose{longdiv}{323\phantom{0}} \\[-3pt]
{\phantom{.0}} \\[-3pt]
\phantom{.} \\[-3pt]
{\phantom{.}} \\[-3pt]
\phantom{000}
\end{array}$
⑦
$\begin{array}{r}
\\[-3pt]
3\enclose{longdiv}{992\phantom{0}} \\[-3pt]
{\phantom{.0}} \\[-3pt]
\phantom{.} \\[-3pt]
{\phantom{.}} \\[-3pt]
\phantom{000}
\end{array}$
⑧
$\begin{array}{r}
\\[-3pt]
6\enclose{longdiv}{33\phantom{0}} \\[-3pt]
{\phantom{.0}} \\[-3pt]
\phantom{.} \\[-3pt]
{\phantom{.}} \\[-3pt]
\phantom{000}
\end{array}$
⑨
$\begin{array}{r}
\\[-3pt]
8\enclose{longdiv}{480\phantom{0}} \\[-3pt]
{\phantom{.0}} \\[-3pt]
\phantom{.} \\[-3pt]
{\phantom{.}} \\[-3pt]
\phantom{000}
\end{array}$
この動画を見る
【レベル３】
①
$\begin{array}{r}
\\[-3pt]
3\enclose{longdiv}{795\phantom{0}} \\[-3pt]
{\phantom{.0}} \\[-3pt]
\phantom{.} \\[-3pt]
{\phantom{.}} \\[-3pt]
\phantom{000}
\end{array}$
②
$\begin{array}{r}
\\[-3pt]
6\enclose{longdiv}{689\phantom{0}} \\[-3pt]
{\phantom{.0}} \\[-3pt]
\phantom{.} \\[-3pt]
{\phantom{.}} \\[-3pt]
\phantom{000}
\end{array}$
③
$\begin{array}{r}
\\[-3pt]
3\enclose{longdiv}{28\phantom{0}} \\[-3pt]
{\phantom{.0}} \\[-3pt]
\phantom{.} \\[-3pt]
{\phantom{.}} \\[-3pt]
\phantom{000}
\end{array}$
【レベル４】
④
$\begin{array}{r}
\\[-3pt]
6\enclose{longdiv}{312\phantom{0}} \\[-3pt]
{\phantom{.0}} \\[-3pt]
\phantom{.} \\[-3pt]
{\phantom{.}} \\[-3pt]
\phantom{000}
\end{array}$
⑤
$\begin{array}{r}
\\[-3pt]
4\enclose{longdiv}{53\phantom{0}} \\[-3pt]
{\phantom{.0}} \\[-3pt]
\phantom{.} \\[-3pt]
{\phantom{.}} \\[-3pt]
\phantom{000}
\end{array}$
⑥
$\begin{array}{r}
\\[-3pt]
3\enclose{longdiv}{323\phantom{0}} \\[-3pt]
{\phantom{.0}} \\[-3pt]
\phantom{.} \\[-3pt]
{\phantom{.}} \\[-3pt]
\phantom{000}
\end{array}$
⑦
$\begin{array}{r}
\\[-3pt]
3\enclose{longdiv}{992\phantom{0}} \\[-3pt]
{\phantom{.0}} \\[-3pt]
\phantom{.} \\[-3pt]
{\phantom{.}} \\[-3pt]
\phantom{000}
\end{array}$
⑧
$\begin{array}{r}
\\[-3pt]
6\enclose{longdiv}{33\phantom{0}} \\[-3pt]
{\phantom{.0}} \\[-3pt]
\phantom{.} \\[-3pt]
{\phantom{.}} \\[-3pt]
\phantom{000}
\end{array}$
⑨
$\begin{array}{r}
\\[-3pt]
8\enclose{longdiv}{480\phantom{0}} \\[-3pt]
{\phantom{.0}} \\[-3pt]
\phantom{.} \\[-3pt]
{\phantom{.}} \\[-3pt]
\phantom{000}
\end{array}$
【小５ 算数】 小５－４０ 分数のたし算・ひき算③ ・ 小数とのコラボ編
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$0.7+\displaystyle \frac{4}{5}=$
②$3\displaystyle \frac{3}{4}-0.5=$
③$2\displaystyle \frac{7}{20}+0.45=$
④$1\displaystyle \frac{8}{15}-0.35=$
⑤$0.6-\displaystyle \frac{1}{3}=$
⑥$\displaystyle \frac{1}{3}+0.75=$
この動画を見る
①$0.7+\displaystyle \frac{4}{5}=$
②$3\displaystyle \frac{3}{4}-0.5=$
③$2\displaystyle \frac{7}{20}+0.45=$
④$1\displaystyle \frac{8}{15}-0.35=$
⑤$0.6-\displaystyle \frac{1}{3}=$
⑥$\displaystyle \frac{1}{3}+0.75=$
【小５ 算数】 小５－３９ 分数のたし算・ひき算② ・ 帯分数編
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$1\displaystyle \frac{3}{5}+\displaystyle \frac{1}{4}=$
②$3\displaystyle \frac{3}{4}-1\displaystyle \frac{5}{12}=$
③$2\displaystyle \frac{2}{3}-2\displaystyle \frac{1}{6}=$
④$1\displaystyle \frac{4}{5}+\displaystyle \frac{7}{10}=$
⑤$3\displaystyle \frac{2}{5}-\displaystyle \frac{1}{2}=$
⑥$2\displaystyle \frac{3}{4}-\displaystyle \frac{7}{8}=$
この動画を見る
①$1\displaystyle \frac{3}{5}+\displaystyle \frac{1}{4}=$
②$3\displaystyle \frac{3}{4}-1\displaystyle \frac{5}{12}=$
③$2\displaystyle \frac{2}{3}-2\displaystyle \frac{1}{6}=$
④$1\displaystyle \frac{4}{5}+\displaystyle \frac{7}{10}=$
⑤$3\displaystyle \frac{2}{5}-\displaystyle \frac{1}{2}=$
⑥$2\displaystyle \frac{3}{4}-\displaystyle \frac{7}{8}=$
【小５ 算数】 小５－３８ 分数のたし算・ひき算① ・ 基本編
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$\displaystyle \frac{3}{7}+\displaystyle \frac{2}{7}=$
②$\displaystyle \frac{2}{3}+\displaystyle \frac{1}{2}=$
③$\displaystyle \frac{7}{5}-\displaystyle \frac{2}{3}=$
④$\displaystyle \frac{4}{5}-\displaystyle \frac{3}{10}=$
⑤$\displaystyle \frac{5}{14}+\displaystyle \frac{1}{2}=$
⑥$\displaystyle \frac{2}{3}-\displaystyle \frac{4}{9}=$
⑦$\displaystyle \frac{3}{4}-\displaystyle \frac{1}{6}+\displaystyle \frac{2}{3}=$
この動画を見る
①$\displaystyle \frac{3}{7}+\displaystyle \frac{2}{7}=$
②$\displaystyle \frac{2}{3}+\displaystyle \frac{1}{2}=$
③$\displaystyle \frac{7}{5}-\displaystyle \frac{2}{3}=$
④$\displaystyle \frac{4}{5}-\displaystyle \frac{3}{10}=$
⑤$\displaystyle \frac{5}{14}+\displaystyle \frac{1}{2}=$
⑥$\displaystyle \frac{2}{3}-\displaystyle \frac{4}{9}=$
⑦$\displaystyle \frac{3}{4}-\displaystyle \frac{1}{6}+\displaystyle \frac{2}{3}=$
【小５ 算数】 小５－３７ 分数の技④ ・ 時間と分数編
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算#数の性質その他
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
分→時間、秒→分にするときには、分母に①＿＿＿＿をつける！
◎時間の単位を変えてみよう！
②7分=＿＿＿＿＿＿＿＿＿＿＿＿時間
③15分=＿＿＿＿＿＿＿＿＿＿＿＿時間
④36秒=＿＿＿＿＿＿＿＿＿＿＿＿分
⑤150秒=＿＿＿＿＿＿＿＿＿＿＿＿分
⑥1時間18分=＿＿＿＿＿＿＿＿＿＿＿＿時間
⑦3時間=＿＿＿＿＿＿＿＿＿＿＿＿分
⑧7分=＿＿＿＿＿＿＿＿＿＿＿＿秒
⑨168秒=＿＿＿＿＿＿＿＿＿＿＿＿分
この動画を見る
分→時間、秒→分にするときには、分母に①＿＿＿＿をつける！
◎時間の単位を変えてみよう！
②7分=＿＿＿＿＿＿＿＿＿＿＿＿時間
③15分=＿＿＿＿＿＿＿＿＿＿＿＿時間
④36秒=＿＿＿＿＿＿＿＿＿＿＿＿分
⑤150秒=＿＿＿＿＿＿＿＿＿＿＿＿分
⑥1時間18分=＿＿＿＿＿＿＿＿＿＿＿＿時間
⑦3時間=＿＿＿＿＿＿＿＿＿＿＿＿分
⑧7分=＿＿＿＿＿＿＿＿＿＿＿＿秒
⑨168秒=＿＿＿＿＿＿＿＿＿＿＿＿分
【小５ 算数】 小５－３６ 分数の技③ ・ 通分編
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①＿＿＿＿をそろえることを通分といって②＿＿＿＿算を使うんだ！
◎( )の中の分数を通分しよう！
③$(\displaystyle \frac{2}{3},\displaystyle \frac{1}{4})=( , )$
④$(\displaystyle \frac{3}{2},\displaystyle \frac{5}{8})=( , )$
⑤$(1\displaystyle \frac{5}{6},2\displaystyle \frac{1}{4})=( , )$
⑥$(\displaystyle \frac{1}{2},\displaystyle \frac{2}{3},\displaystyle \frac{5}{9})=( , )$
◎$□$にあてはまる等号や不等号を書こう！
⑦$\displaystyle \frac{3}{5}□\displaystyle \frac{2}{3}$
⑧$\displaystyle \frac{3}{4}□\displaystyle \frac{7}{12}$
⑨$\displaystyle \frac{10}{15}□\displaystyle \frac{6}{9}$
この動画を見る
①＿＿＿＿をそろえることを通分といって②＿＿＿＿算を使うんだ！
◎( )の中の分数を通分しよう！
③$(\displaystyle \frac{2}{3},\displaystyle \frac{1}{4})=( , )$
④$(\displaystyle \frac{3}{2},\displaystyle \frac{5}{8})=( , )$
⑤$(1\displaystyle \frac{5}{6},2\displaystyle \frac{1}{4})=( , )$
⑥$(\displaystyle \frac{1}{2},\displaystyle \frac{2}{3},\displaystyle \frac{5}{9})=( , )$
◎$□$にあてはまる等号や不等号を書こう！
⑦$\displaystyle \frac{3}{5}□\displaystyle \frac{2}{3}$
⑧$\displaystyle \frac{3}{4}□\displaystyle \frac{7}{12}$
⑨$\displaystyle \frac{10}{15}□\displaystyle \frac{6}{9}$
【小５ 算数】 小５－３５ 分数の技② ・ 約分編
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
分母と分子を同じ数で①＿＿＿＿ことを約分っていうんだ！
◎次の文数を約分しよう！
②$\displaystyle \frac{4}{6}=$
③$\displaystyle \frac{24}{16}=$
④$2\displaystyle \frac{15}{18}=$
⑤$\displaystyle \frac{21}{28}=$
⑥$\displaystyle \frac{56}{72}=$
⑦$\displaystyle \frac{84}{156}=$
⑧次の文数の中で$\displaystyle \frac{9}{12}$と同じ大きさの分数に〇をつけよう！
$\displaystyle \frac{4}{5}, \displaystyle \frac{6}{8}, \displaystyle \frac{10}{15},
\displaystyle \frac{10}{13}, \displaystyle \frac{3}{4}$
この動画を見る
分母と分子を同じ数で①＿＿＿＿ことを約分っていうんだ！
◎次の文数を約分しよう！
②$\displaystyle \frac{4}{6}=$
③$\displaystyle \frac{24}{16}=$
④$2\displaystyle \frac{15}{18}=$
⑤$\displaystyle \frac{21}{28}=$
⑥$\displaystyle \frac{56}{72}=$
⑦$\displaystyle \frac{84}{156}=$
⑧次の文数の中で$\displaystyle \frac{9}{12}$と同じ大きさの分数に〇をつけよう！
$\displaystyle \frac{4}{5}, \displaystyle \frac{6}{8}, \displaystyle \frac{10}{15},
\displaystyle \frac{10}{13}, \displaystyle \frac{3}{4}$
【小５ 算数】 小５－３４ 分数の技① ・ 基本編
単元：
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
分数は、分母と分子を①＿＿＿＿でかけたり、わったりしていいんだよ！
◎$□$にあてはまる数を書こう！
②$\displaystyle \frac{3}{4}=\displaystyle \frac{□}{8}$
③$\displaystyle \frac{2}{3}=\displaystyle \frac{□}{9}$
④$\displaystyle \frac{10}{12}=\displaystyle \frac{□}{6}$
⑤$\displaystyle \frac{1}{5}=\displaystyle \frac{□}{10}=\displaystyle \frac{4}{□}$
⑥$\displaystyle \frac{6}{9}=\displaystyle \frac{□}{3}=\displaystyle \frac{□}{15}$
⑦$\displaystyle \frac{6}{12}=\displaystyle \frac{□}{14}$
この動画を見る
分数は、分母と分子を①＿＿＿＿でかけたり、わったりしていいんだよ！
◎$□$にあてはまる数を書こう！
②$\displaystyle \frac{3}{4}=\displaystyle \frac{□}{8}$
③$\displaystyle \frac{2}{3}=\displaystyle \frac{□}{9}$
④$\displaystyle \frac{10}{12}=\displaystyle \frac{□}{6}$
⑤$\displaystyle \frac{1}{5}=\displaystyle \frac{□}{10}=\displaystyle \frac{4}{□}$
⑥$\displaystyle \frac{6}{9}=\displaystyle \frac{□}{3}=\displaystyle \frac{□}{15}$
⑦$\displaystyle \frac{6}{12}=\displaystyle \frac{□}{14}$