 算数(中学受験)
算数(中学受験)
 算数(中学受験)
算数(中学受験)
【受験算数】右の図のように、内側の一辺が12個であるよう5列の中空方陣をご石で作り、くさり状につないだ。(1)この外側のご石は何個か。(2)ご石の総数は何個か。

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図のように、内側の一辺が12個であるよう5列の中空方陣をご石で作り、くさり状につないだ。
(1)この外側のご石は何個か。
(2)ご石の総数は何個か。
この動画を見る
右の図のように、内側の一辺が12個であるよう5列の中空方陣をご石で作り、くさり状につないだ。
(1)この外側のご石は何個か。
(2)ご石の総数は何個か。
【受験算数】右の図のように、内側の一辺が6個であるよう3列の中空方陣をご石で作り、くさり状につないだ。(1)この外側のご石は何個か。(2)ご石の総数は何個か。

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図のように、内側の一辺が6個であるよう3列の中空方陣をご石で作り、くさり状につないだ。
(1)この外側のご石は何個か。
(2)ご石の総数は何個か。
この動画を見る
右の図のように、内側の一辺が6個であるよう3列の中空方陣をご石で作り、くさり状につないだ。
(1)この外側のご石は何個か。
(2)ご石の総数は何個か。
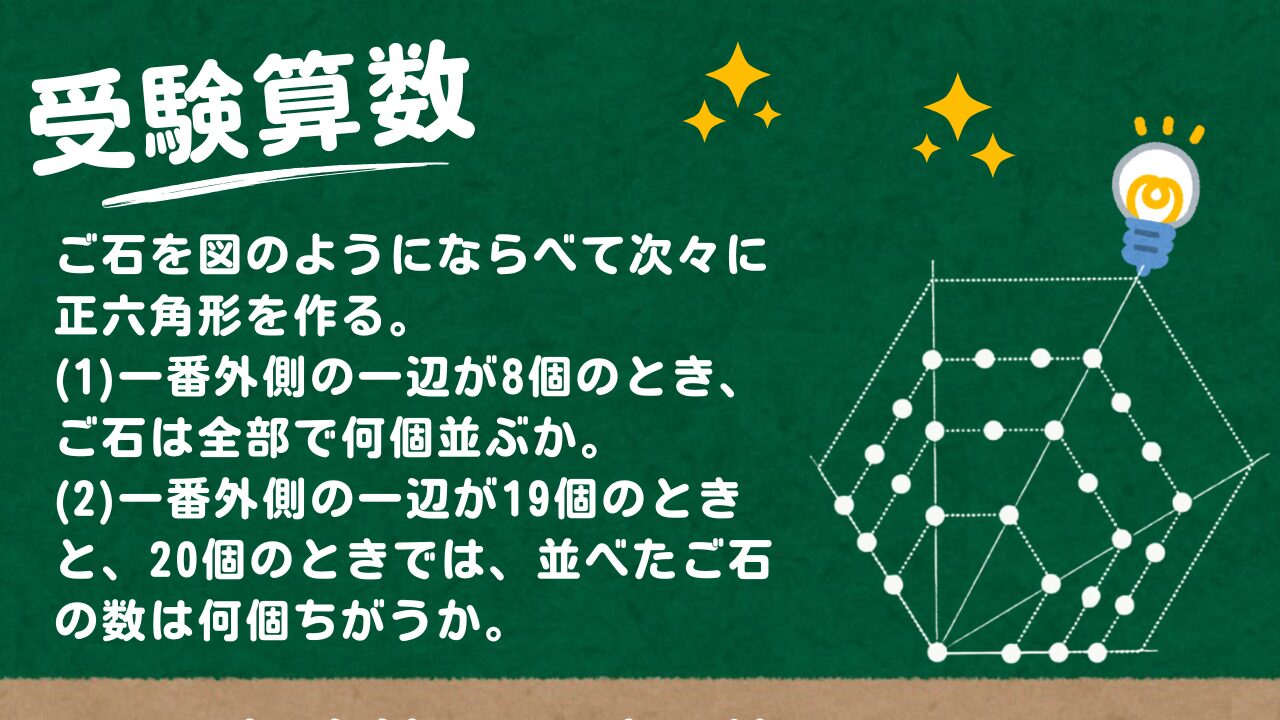
【受験算数】ご石を図のようにならべて次々に正六角形を作る。(1)一番外側の一辺が8個のとき、ご石は全部で何個並ぶか。(2)一番外側の一辺が19個のときと、20個のときでは、並べたご石の数は何個ちがうか
単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
ご石を図のようにならべて次々に正六角形を作る。
(1)一番外側の一辺が8個のとき、ご石は全部で何個並ぶか。
(2)一番外側の一辺が19個のときと、20個のときでは、並べたご石の数は何個ちがうか。
この動画を見る
ご石を図のようにならべて次々に正六角形を作る。
(1)一番外側の一辺が8個のとき、ご石は全部で何個並ぶか。
(2)一番外側の一辺が19個のときと、20個のときでは、並べたご石の数は何個ちがうか。
【受験算数】ご石を図のようにならべて次々に正五角形を作る。(1)一番外側の一辺が9個のとき、ご石は全部で何個並ぶか。(2)一番外側の一辺が16個のときと、17個のときでは、並べたご石の数は何個ちがうか

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
ご石を図のようにならべて次々に正五角形を作る。
(1)一番外側の一辺が9個のとき、ご石は全部で何個並ぶか。
(2)一番外側の一辺が16個のときと、17個のときでは、並べたご石の数は何個ちがうか。
この動画を見る
ご石を図のようにならべて次々に正五角形を作る。
(1)一番外側の一辺が9個のとき、ご石は全部で何個並ぶか。
(2)一番外側の一辺が16個のときと、17個のときでは、並べたご石の数は何個ちがうか。
【受験算数】長方形の土地がある。この土地の北側には6mごとに、西側には8mごとに木を植える計画を立て、その分にあたるなえ木を61本買った。実際は、どちらの側にも7.5mごとに植えたので、なえ木が8本…

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
長方形の土地がある。この土地の北側には6mごとに、西側には8mごとに木を植える計画を立て、その分にあたるなえ木を61本買った。実際は、どちらの側にも7.5mごとに植えたので、なえ木が8本残った。土地のかどには必ずなえ木を植えるように計画し、実際に植えました。この土地の面積は何aか。
この動画を見る
長方形の土地がある。この土地の北側には6mごとに、西側には8mごとに木を植える計画を立て、その分にあたるなえ木を61本買った。実際は、どちらの側にも7.5mごとに植えたので、なえ木が8本残った。土地のかどには必ずなえ木を植えるように計画し、実際に植えました。この土地の面積は何aか。
【受験算数】長方形の土地がある。この土地の北側には2mごとに、西側には4mごとに木を植える計画を立て、その分にあたるなえ木を81本買った。実際は、どちらの側にも5mごとに植えたので、なえ木が38本…

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
長方形の土地がある。この土地の北側には2mごとに、西側には4mごとに木を植える計画を立て、その分にあたるなえ木を81本買った。実際は、どちらの側にも5mごとに植えたので、なえ木が38本残った。土地のかどには必ずなえ木を植えるように計画し、実際に植えた。この土地の面積は何aか。
この動画を見る
長方形の土地がある。この土地の北側には2mごとに、西側には4mごとに木を植える計画を立て、その分にあたるなえ木を81本買った。実際は、どちらの側にも5mごとに植えたので、なえ木が38本残った。土地のかどには必ずなえ木を植えるように計画し、実際に植えた。この土地の面積は何aか。
【受験算数】チョコレートのいちばん外側のつつみ紙を6枚集めると、新しいチョコレート1個といつでも引きかえられるようなチョコレートがあるとします。次の問いに答えよ。このチョコレートを123個買った人が…

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
チョコレートのいちばん外側のつつみ紙を6枚集めると、新しいチョコレート1個といつでも引きかえられるようなチョコレートがあるとします。次の問いに答えよ。
(1)このチョコレートを123個買った人が、つつみ紙で引きかえられるものはすべて引きかえるとすると、買ったものも合わせて全部で何個のチョコレートを手に入れることができるか。
(2)300個のチョコレートを手に入れるためには、少なくとも何個のチョコレートを買えばよいか。
この動画を見る
チョコレートのいちばん外側のつつみ紙を6枚集めると、新しいチョコレート1個といつでも引きかえられるようなチョコレートがあるとします。次の問いに答えよ。
(1)このチョコレートを123個買った人が、つつみ紙で引きかえられるものはすべて引きかえるとすると、買ったものも合わせて全部で何個のチョコレートを手に入れることができるか。
(2)300個のチョコレートを手に入れるためには、少なくとも何個のチョコレートを買えばよいか。
【受験算数】チョコレートのいちばん外側のつつみ紙を4枚集めると、新しいチョコレート1個といつでも引きかえられるようなチョコレートがある。このチョコレートを35個買った人が、つつみ紙で引きかえ…

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
チョコレートのいちばん外側のつつみ紙を4枚集めると、新しいチョコレート1個といつでも引きかえられるようなチョコレートがある。
(1)このチョコレートを35個買った人が、つつみ紙で引きかえられるものはすべて引きかえるとすると、買ったものも合わせて全部で何個のチョコレートを手に入れることができるか。
(2)135個のチョコレートを手に入れるためには、少なくとも何個のチョコレートを買えばよいか。
この動画を見る
チョコレートのいちばん外側のつつみ紙を4枚集めると、新しいチョコレート1個といつでも引きかえられるようなチョコレートがある。
(1)このチョコレートを35個買った人が、つつみ紙で引きかえられるものはすべて引きかえるとすると、買ったものも合わせて全部で何個のチョコレートを手に入れることができるか。
(2)135個のチョコレートを手に入れるためには、少なくとも何個のチョコレートを買えばよいか。
【受験算数】一辺の長さが整数であるような正方形のたてと横を1cmはばに等分して、いくつかの小さな正方形にわける。左上のすみに1を書き、その下へ順に2,3,4,5,…という数を書き入れる。突きあたる…

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
一辺の長さが整数であるような正方形のたてと横を1cmはばに等分して、いくつかの小さな正方形にわける。左上のすみに1を書き、その下へ順に2,3,4,5,…という数を書き入れる。突きあたるごとに直角にまがり、うずまき状に進む。例えば(A)図は、一辺5cmの正方形について、この方法で書き入れたもの。(B)図は一辺がxcmの正方形について同じ方法で書き入れたものの一部だけを見せたもの。図(B)について、次の問いに答えよ。
(1)この正方形の一辺xcmを求めよ
(2)この正方形に書き入れてある数のうちで、いちばん大きい数は何か
(3)アのところに書いてある数は何か
この動画を見る
一辺の長さが整数であるような正方形のたてと横を1cmはばに等分して、いくつかの小さな正方形にわける。左上のすみに1を書き、その下へ順に2,3,4,5,…という数を書き入れる。突きあたるごとに直角にまがり、うずまき状に進む。例えば(A)図は、一辺5cmの正方形について、この方法で書き入れたもの。(B)図は一辺がxcmの正方形について同じ方法で書き入れたものの一部だけを見せたもの。図(B)について、次の問いに答えよ。
(1)この正方形の一辺xcmを求めよ
(2)この正方形に書き入れてある数のうちで、いちばん大きい数は何か
(3)アのところに書いてある数は何か
【受験算数】一辺の長さが整数であるような正方形のたてと横を1cmはばに等分して、いくつかの小さな正方形にわける。左上のすみに1を書き、その下へ順に2,3,4,5,…という数を書き入れる。突きあたる…

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
一辺の長さが整数であるような正方形のたてと横を1cmはばに等分して、いくつかの小さな正方形にわける。左上のすみに1を書き、その下へ順に2,3,4,5,…という数を書き入れる。突きあたるごとに直角にまがり、うずまき状に進む。例えば(A)図は、一辺5cmの正方形について、この方法で書き入れたもの。(B)図は一辺がxcmの正方形について同じ方法で書き入れたものの一部だけを見せたもの。図(B)について、次の問いに答えよ。
(1)この正方形の一辺xcmを求めよ
(2)この正方形に書き入れてある数のうちで、いちばん大きい数は何か
(3)アのところに書いてある数は何か
この動画を見る
一辺の長さが整数であるような正方形のたてと横を1cmはばに等分して、いくつかの小さな正方形にわける。左上のすみに1を書き、その下へ順に2,3,4,5,…という数を書き入れる。突きあたるごとに直角にまがり、うずまき状に進む。例えば(A)図は、一辺5cmの正方形について、この方法で書き入れたもの。(B)図は一辺がxcmの正方形について同じ方法で書き入れたものの一部だけを見せたもの。図(B)について、次の問いに答えよ。
(1)この正方形の一辺xcmを求めよ
(2)この正方形に書き入れてある数のうちで、いちばん大きい数は何か
(3)アのところに書いてある数は何か
【受験算数】 1から240までの数を書いたカード240枚を上から数の小さい順に並べる。これをそのまま手にもって、上から順に左、右、左、右、...と交互に配り、配った順に上につみ重ねていって、240枚…

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
1から240までの数を書いたカード240枚を上から数の小さい順に並べる。これをそのまま手にもって、上から順に左、右、左、右、...と交互に配り、配った順に上につみ重ねていって、240枚のカードを2つの山に分け、左側の山のカードは捨てて、右側の山のカードを再び数の小さい順に並べる。ここまでの操作を1回として、この操作をカードがなくなるまで続ける。
(1)この操作を3回くり返したとき、残っているカードは何枚か。このとき上から4枚目のカードに書かれた数はいくつか。
(2)この操作を何回くり返すと、残ったカードの数の和がはじめて400より小さくなるか。
(3)1枚のカードが残るまでに、何回この操作をくり返すか。そのカードに書かれた数を答えよ。
この動画を見る
1から240までの数を書いたカード240枚を上から数の小さい順に並べる。これをそのまま手にもって、上から順に左、右、左、右、...と交互に配り、配った順に上につみ重ねていって、240枚のカードを2つの山に分け、左側の山のカードは捨てて、右側の山のカードを再び数の小さい順に並べる。ここまでの操作を1回として、この操作をカードがなくなるまで続ける。
(1)この操作を3回くり返したとき、残っているカードは何枚か。このとき上から4枚目のカードに書かれた数はいくつか。
(2)この操作を何回くり返すと、残ったカードの数の和がはじめて400より小さくなるか。
(3)1枚のカードが残るまでに、何回この操作をくり返すか。そのカードに書かれた数を答えよ。
【受験算数】1から127までの数を書いたカード127枚を上から数の小さい順に並べる。これをそのまま手にもって、上から順に左、右、左、右、...と交互に配り、配った順に上につみ重ねていって、127枚の…

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
1から127までの数を書いたカード127枚を上から数の小さい順に並べる。これをそのまま手にもって、上から順に左、右、左、右、...と交互に配り、配った順に上につみ重ねていって、127枚のカードを2つの山に分け、左側の山のカードは捨てて、右側の山のカードを再び数の小さい順に並べる。ここまでの操作を1回として、この操作をカードがなくなるまで続ける。
(1)この操作を2回くり返したとき、残っているカードは何枚か。このとき上から5枚目のカードに書かれた数を答えよ。
(2)この操作を何回くり返すと、残ったカードの数の和がはじめて400より小さくなるか。
(3)1枚のカードが残るまでに、何回この操作をくり返すか。そのカードに書かれた数を答えよ。
この動画を見る
1から127までの数を書いたカード127枚を上から数の小さい順に並べる。これをそのまま手にもって、上から順に左、右、左、右、...と交互に配り、配った順に上につみ重ねていって、127枚のカードを2つの山に分け、左側の山のカードは捨てて、右側の山のカードを再び数の小さい順に並べる。ここまでの操作を1回として、この操作をカードがなくなるまで続ける。
(1)この操作を2回くり返したとき、残っているカードは何枚か。このとき上から5枚目のカードに書かれた数を答えよ。
(2)この操作を何回くり返すと、残ったカードの数の和がはじめて400より小さくなるか。
(3)1枚のカードが残るまでに、何回この操作をくり返すか。そのカードに書かれた数を答えよ。
【受験算数】たかし君は、所持金の40%で本を買いました。次に、残りの所持金の5/9で文ぼう具を買ったところ、残りの所持金ははじめの所持金の1/3よりも240円少なくなりました。文ぼう具の代金は…

単元:
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題
教材:
#予習シ#予習シ算数・小5上#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
たかし君は、所持金の40%で本を買いました。次に、残りの所持金の5/9で文ぼう具を買ったところ、残りの所持金ははじめの所持金の1/3よりも240円少なくなりました。これについて、 次の問いに答えなさい。
(1) 文ぼう具の代金は、はじめの所持金の何分のいくつですか。分数で答えなさい。
(2) はじめの所持金は何円でしたか。
この動画を見る
たかし君は、所持金の40%で本を買いました。次に、残りの所持金の5/9で文ぼう具を買ったところ、残りの所持金ははじめの所持金の1/3よりも240円少なくなりました。これについて、 次の問いに答えなさい。
(1) 文ぼう具の代金は、はじめの所持金の何分のいくつですか。分数で答えなさい。
(2) はじめの所持金は何円でしたか。
【受験算数】120をわると12あまり、85をわると13あまる整数のうち、最も小さい整数はいくつですか。9でわると5あまり、13でわると9あまる整数のうち、1000に最も近い整数はいくつですか。

単元:
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題
教材:
#予習シ#予習シ算数・小5上#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の問いに答えなさい。
(1) 120をわると12あまり、85をわると13あまる整数のうち、最も小さい整数はいくつですか。
(2) 9でわると5あまり、13でわると9あまる整数のうち、1000に最も近い整数はいくつですか。
この動画を見る
次の問いに答えなさい。
(1) 120をわると12あまり、85をわると13あまる整数のうち、最も小さい整数はいくつですか。
(2) 9でわると5あまり、13でわると9あまる整数のうち、1000に最も近い整数はいくつですか。
【受験算数】右の図は、正方形の中に三角形をかいたものです。色のついた部分の面積は何㎠ですか。

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#予習シ#予習シ算数・小5上#中学受験教材#平面図形
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図は、正方形の中に三角形をかいたものです。
色のついた部分の面積は何㎠ですか。
この動画を見る
右の図は、正方形の中に三角形をかいたものです。
色のついた部分の面積は何㎠ですか。
【受験算数】野球の大会に40チームが出場します。大会は、はじめに5チームずつのグループに分かれて、 各グループごとにリーグ戦で予選が行われます。そして、各グループの上位2チームずつが本戦に勝ち残り…

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#予習シ#予習シ算数・小5上#中学受験教材#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
野球の大会に40チームが出場します。大会は、はじめに5チームずつのグループに分かれて、 各グループごとにリーグ戦で予選が行われます。そして、各グループの上位2チームずつが本戦に勝ち残り、本戦はトーナメント戦で優勝が決まります。この大会では、全部で何試合行われますか。ただし、予選のリーグ戦は、グループ内の他のチームと1試合ずつ行います。また、 どの試合も引き分けはなく、3位決定戦などは行わないものとします。
この動画を見る
野球の大会に40チームが出場します。大会は、はじめに5チームずつのグループに分かれて、 各グループごとにリーグ戦で予選が行われます。そして、各グループの上位2チームずつが本戦に勝ち残り、本戦はトーナメント戦で優勝が決まります。この大会では、全部で何試合行われますか。ただし、予選のリーグ戦は、グループ内の他のチームと1試合ずつ行います。また、 どの試合も引き分けはなく、3位決定戦などは行わないものとします。
【受験算数】1, 1, 2, 3, 4, 5 の6枚のカードがあります。この中から3枚を取り出してならべ。3けたの整数を作ります。これについて、次の問いに答えなさい。4の倍数は何通りできますか…

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#予習シ#予習シ算数・小5上#中学受験教材#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
1, 1, 2, 3, 4, 5 の6枚のカードがあります。この中から3枚を取り出してならべ。3けたの整数を作ります。これについて、次の問いに答えなさい。
(1)4の倍数は何通りできますか。
(2)3の倍数は何通りできますか。
この動画を見る
1, 1, 2, 3, 4, 5 の6枚のカードがあります。この中から3枚を取り出してならべ。3けたの整数を作ります。これについて、次の問いに答えなさい。
(1)4の倍数は何通りできますか。
(2)3の倍数は何通りできますか。
【受験算数】A, B, C, D, E, F, Gの7人が旅行に行き、旅館にとまることになりました。旅館では、3人がとまれる「鶴の間」と、4人がとまれる「亀の間」の2部屋に分かれてとまることにします…

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#予習シ#予習シ算数・小5上#中学受験教材#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
A, B, C, D, E, F, Gの7人が旅行に行き、旅館にとまることになりました。旅館では、3人がとまれる「鶴の間」と、4人がとまれる「亀の間」の2部屋に分かれてとまることにします。これについて、次の問いに答えなさい。
(1)とまり方は何通りありますか。
(2)AとBが同じ部屋になるとまり方は何通りありますか。
この動画を見る
A, B, C, D, E, F, Gの7人が旅行に行き、旅館にとまることになりました。旅館では、3人がとまれる「鶴の間」と、4人がとまれる「亀の間」の2部屋に分かれてとまることにします。これについて、次の問いに答えなさい。
(1)とまり方は何通りありますか。
(2)AとBが同じ部屋になるとまり方は何通りありますか。
【受験算数】5枚の同じコインを、A, B, Cの3人で分けます。(1)全員、必ず1枚はもらえるとすると、分け方は何通りありますか(2) 1枚ももらえない人がいてもよいとすると、分け方は何通りありますか

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#予習シ#予習シ算数・小5上#中学受験教材#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
5枚の同じコインを、A, B, Cの3人で分けます。これについて、次の問いに答えなさい。
(1)全員、必ず1枚はもらえるとすると、分け方は何通りありますか。
(2) 1枚ももらえない人がいてもよいとすると、分け方は何通りありますか。
この動画を見る
5枚の同じコインを、A, B, Cの3人で分けます。これについて、次の問いに答えなさい。
(1)全員、必ず1枚はもらえるとすると、分け方は何通りありますか。
(2) 1枚ももらえない人がいてもよいとすると、分け方は何通りありますか。
【受験算数】右の図で、5つの直線ア、イ、ウ、エ、オは互いに平行で、4つの直線力、キ、ク、ケは互いに平行です。この図の中に平行四辺形は何個ありますか。

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#予習シ#予習シ算数・小5上#中学受験教材#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図で、5つの直線ア、イ、ウ、エ、オは互いに平行で、4つの直線力、キ、ク、ケは互いに平行です。この図の中に平行四辺形は何個ありますか。
この動画を見る
右の図で、5つの直線ア、イ、ウ、エ、オは互いに平行で、4つの直線力、キ、ク、ケは互いに平行です。この図の中に平行四辺形は何個ありますか。
【受験算数】A, B, C, D, E, F, Gの7人の男子とP, Q, R, Sの4人の女子がいます。男子から3人、女子から2人の合計5人を音楽係として選ぶ方法は何通りありますか。

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#予習シ#予習シ算数・小5上#中学受験教材#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
A, B, C, D, E, F, Gの7人の男子とP, Q, R, Sの4人の女子がいます。
これについて、次の問いに答えなさい。
(1) 男子から3人、女子から2人の合計5人を音楽係として選ぶ方法は何通りありますか。
(2)この11人を、指揮者1人、リコーダー担当8人、ハーモニカ担当2人に分けるとき、分け方は何通りありますか。
この動画を見る
A, B, C, D, E, F, Gの7人の男子とP, Q, R, Sの4人の女子がいます。
これについて、次の問いに答えなさい。
(1) 男子から3人、女子から2人の合計5人を音楽係として選ぶ方法は何通りありますか。
(2)この11人を、指揮者1人、リコーダー担当8人、ハーモニカ担当2人に分けるとき、分け方は何通りありますか。
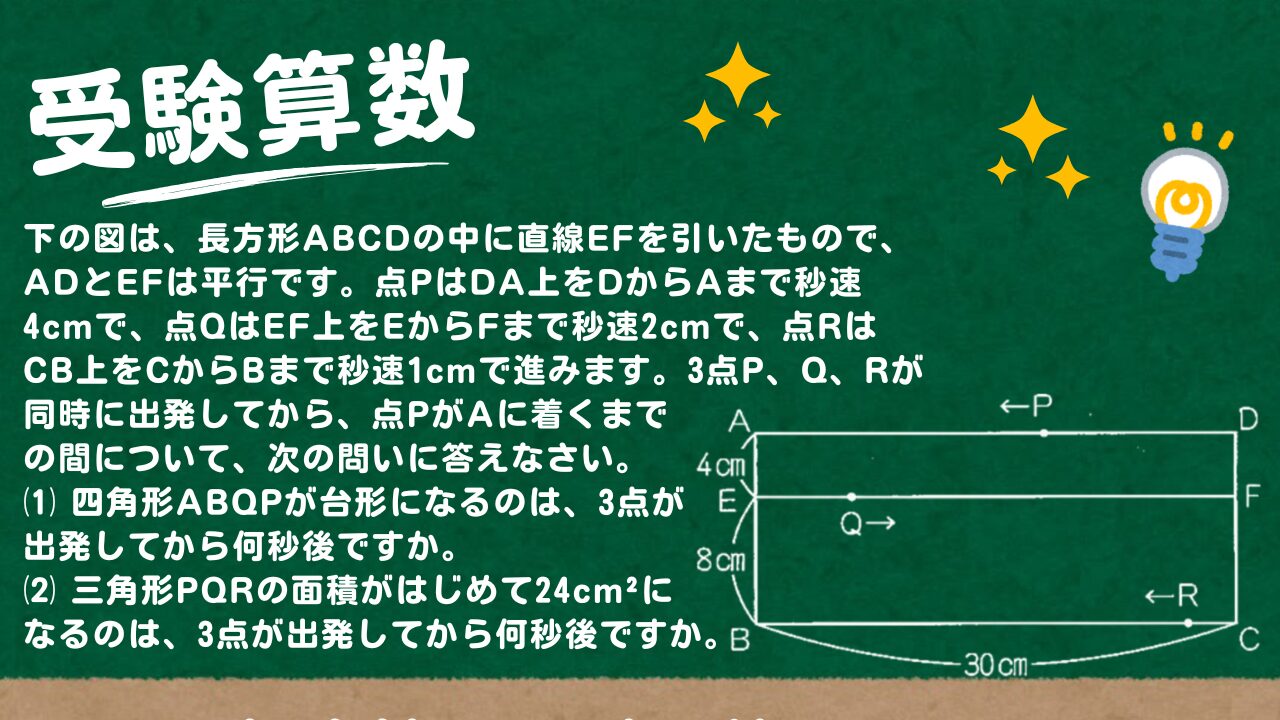
【受験算数】下の図は、長方形ABCDの中に直線EFを引いたもので、ADとEFは平行です。点PはDA上をDからAまで秒速4cmで、点QはEF上をEからFまで秒速2cmで、点RはCB上をCからBまで…
単元:
#算数(中学受験)#速さ#点の移動・時計算
教材:
#予習シ#予習シ・算数・小6上#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
下の図は、長方形ABCDの中に直線EFを引いたもので、ADとEFは平行です。点PはDA上をDからAまで秒速4cmで、点QはEF上をEからFまで秒速2cmで、点RはCB上をCからBまで秒速1cmで進みます。3点P、Q、Rが同時に出発してから、点PがAに着くまでの間について、次の問いに答えなさい。
⑴ 四角形ABQPが台形になるのは、3点が出発してから何秒後ですか。
⑵ 三角形PQRの面積がはじめて24cm²になるのは、3点が出発してから何秒後ですか。
この動画を見る
下の図は、長方形ABCDの中に直線EFを引いたもので、ADとEFは平行です。点PはDA上をDからAまで秒速4cmで、点QはEF上をEからFまで秒速2cmで、点RはCB上をCからBまで秒速1cmで進みます。3点P、Q、Rが同時に出発してから、点PがAに着くまでの間について、次の問いに答えなさい。
⑴ 四角形ABQPが台形になるのは、3点が出発してから何秒後ですか。
⑵ 三角形PQRの面積がはじめて24cm²になるのは、3点が出発してから何秒後ですか。
【受験算数】下の図のように、半径5cmの円Oがあります。2つの円P,Qの半径はどちらも1cmで、PはOの外側にそって、QはOの内側にそってそれぞれすべらないように転がって1周し、もとの位置に戻ります。

単元:
#算数(中学受験)#平面図形#図形の移動
教材:
#予習シ#予習シ・算数・小6上#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
下の図のように、半径5cmの円Oがあります。2つの円P,Qの半径はどちらも1cmで、PはOの外側にそって、QはOの内側にそってそれぞれすべらないように転がって1周し、もとの位置に戻ります。これについて次の問に答えなさい。
1)PがOの外側にそって1周する間にP自身は何回転しますか?
2)QがOの内側にそって1周する間にQ自身は何回転しますか?
この動画を見る
下の図のように、半径5cmの円Oがあります。2つの円P,Qの半径はどちらも1cmで、PはOの外側にそって、QはOの内側にそってそれぞれすべらないように転がって1周し、もとの位置に戻ります。これについて次の問に答えなさい。
1)PがOの外側にそって1周する間にP自身は何回転しますか?
2)QがOの内側にそって1周する間にQ自身は何回転しますか?
【受験算数】原価が400円の品物に520円の定価をつけて売りました。仕入れた品物の個数全体の75%より2個多く売れたとき、売り上げた金額は仕入れた金額に等しくなりました。仕入れた品物は何個ですか?

単元:
#算数(中学受験)#文章題#売買損益と食塩水
教材:
#予習シ#予習シ・算数・小6上#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
原価が400円の品物に520円の定価をつけて売りました。仕入れた品物の個数全体の75%より2個多く売れたとき、売り上げた金額は仕入れた金額に等しくなりました。仕入れた品物は何個ですか?
この動画を見る
原価が400円の品物に520円の定価をつけて売りました。仕入れた品物の個数全体の75%より2個多く売れたとき、売り上げた金額は仕入れた金額に等しくなりました。仕入れた品物は何個ですか?
【受験算数】下の図のようにすべての辺の長さが等しい三角すいAーBCDがあります。辺AC、ADをそれぞれ3等分点のうち、頂点C、Dに近い方の点をそれぞれ点P、Qとし、点Rは辺AB上の点とします。この…

単元:
#算数(中学受験)#立体図形#立体切断#体積・表面積・回転体・水量・変化のグラフ
教材:
#予習シ#予習シ・算数・小6上#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
下の図のようにすべての辺の長さが等しい三角すいAーBCDがあります。辺AC、ADをそれぞれ3等分点のうち、頂点C、Dに近い方の点をそれぞれ点P、Qとし、点Rは辺AB上の点とします。
この立体を点P、Q、Rで切ったとき、頂点Aを含む方の立体の体積は三角すいA―BCDの体積の1/3になりました。このとき、AR:RBを求めなさい。
この動画を見る
下の図のようにすべての辺の長さが等しい三角すいAーBCDがあります。辺AC、ADをそれぞれ3等分点のうち、頂点C、Dに近い方の点をそれぞれ点P、Qとし、点Rは辺AB上の点とします。
この立体を点P、Q、Rで切ったとき、頂点Aを含む方の立体の体積は三角すいA―BCDの体積の1/3になりました。このとき、AR:RBを求めなさい。
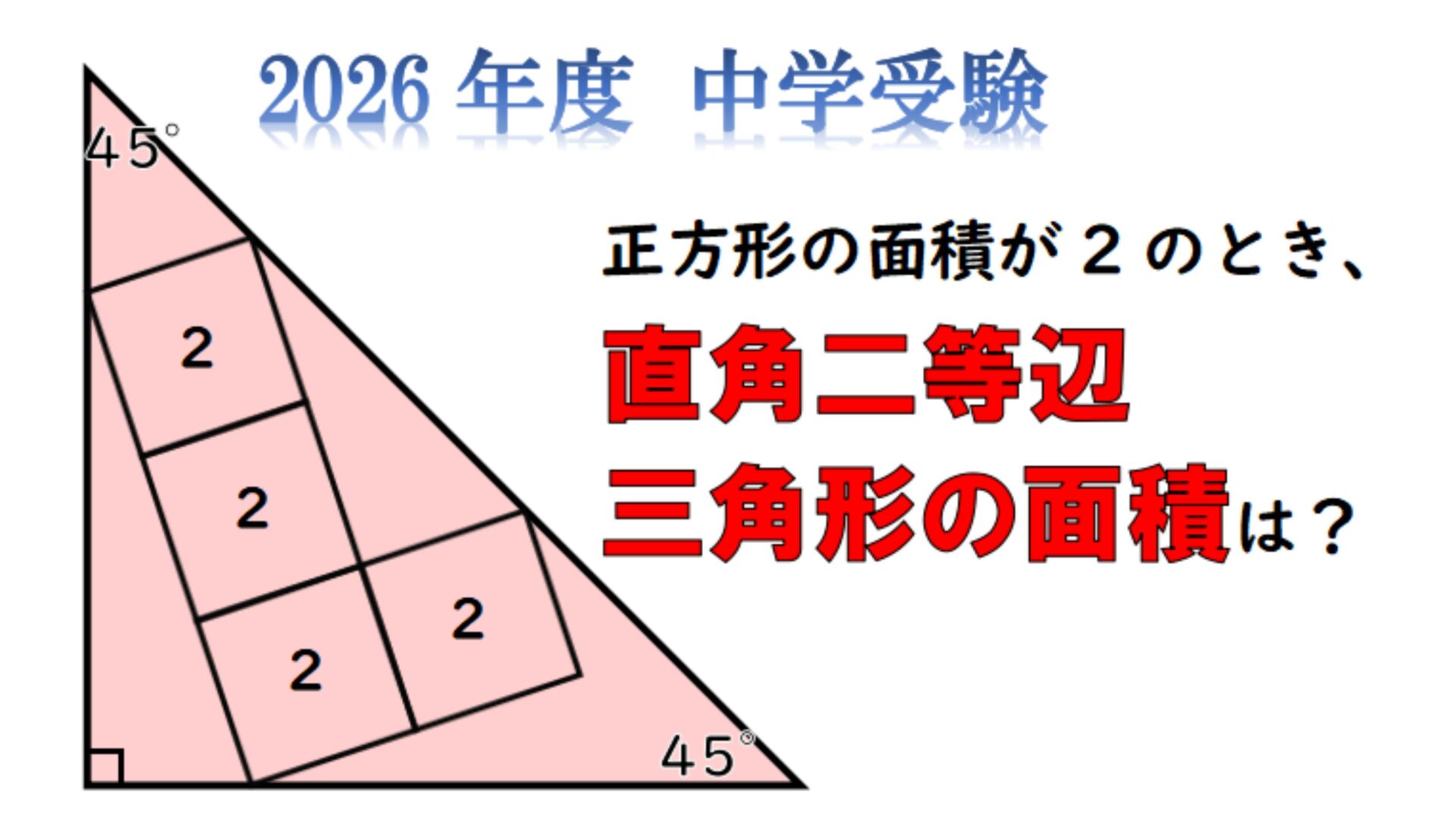
【受験算数】2026年度 中学入試 平面図形 大宮開成中
【受験算数】下の図のかげをつけた図形は、1辺6cmの正方形を3個組み合わせたものです。1辺6cmの正三角形ABCをこの図形の辺にそって、アの位置から矢印の方向にイの位置まですべらないように転がし…

単元:
#算数(中学受験)#平面図形#図形の移動#平面図形その他
教材:
#予習シ#予習シ・算数・小6上#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
下の図のかげをつけた図形は、1辺6cmの正方形を3個組み合わせたものです。
1辺6cmの正三角形ABCをこの図形の辺にそって、アの位置から矢印の方向にイの位置まですべらないように転がしました。これについて次の問に答えなさい。
1)頂点Aが動いたあとの線の長さは何cmですか?
2)正三角形ABCが動いたあとの図形の面積は何㎠ですか?
この動画を見る
下の図のかげをつけた図形は、1辺6cmの正方形を3個組み合わせたものです。
1辺6cmの正三角形ABCをこの図形の辺にそって、アの位置から矢印の方向にイの位置まですべらないように転がしました。これについて次の問に答えなさい。
1)頂点Aが動いたあとの線の長さは何cmですか?
2)正三角形ABCが動いたあとの図形の面積は何㎠ですか?
【受験算数】下の図で、図形アは半径8cm四分円OPQです。はじめ、円イの円周上の点RがPと重なるように置き、円イが矢印の向きにすべることなく転がります。点Rが再びおうぎ形の周状にきたとき、点Rは…

単元:
#算数(中学受験)#平面図形#図形の移動#平面図形その他
教材:
#予習シ#予習シ・算数・小6上#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
下の図で、図形アは半径8cm四分円OPQです。はじめ、円イの円周上の点RがPと重なるように置き、円イが矢印の向きにすべることなく転がります。点Rが再びおうぎ形の周状にきたとき、点RはQと重なりました。円イは図形アのまわりを1周してもとの位置に戻ったところで止まりました。このとき、円イが動いたあとの図形の面積は何cm²ですか。ただし、点Rはもとの位置に戻るとは限りません。
この動画を見る
下の図で、図形アは半径8cm四分円OPQです。はじめ、円イの円周上の点RがPと重なるように置き、円イが矢印の向きにすべることなく転がります。点Rが再びおうぎ形の周状にきたとき、点RはQと重なりました。円イは図形アのまわりを1周してもとの位置に戻ったところで止まりました。このとき、円イが動いたあとの図形の面積は何cm²ですか。ただし、点Rはもとの位置に戻るとは限りません。
【受験算数】第1問あるきまりにしたがって、数が並んでいます。□にあてはまる数を答えなさい。(1)1,5,9,13,17,□,25,…(2)1,3,9,27,81,□,729,…

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
第1問
あるきまりにしたがって、数が並んでいます。□にあてはまる数を答えなさい。
(1)1,5,9,13,17,□,25,…
(2)1,3,9,27,81,□,729,…
(3)1,3,6,10,15,□,28,…
(4)1,4,9,16,25,□,49,…
第2問
あるきまりにしたがって、数が並んでいます。□にあてはまる数を答えなさい。
(1)1,5,9,13,17,□,25,…
(2)1,3,9,27,81,□,729,…
(3)1,3,6,10,15,□,28,…
(4)1,4,9,16,25,□,49,…
この動画を見る
第1問
あるきまりにしたがって、数が並んでいます。□にあてはまる数を答えなさい。
(1)1,5,9,13,17,□,25,…
(2)1,3,9,27,81,□,729,…
(3)1,3,6,10,15,□,28,…
(4)1,4,9,16,25,□,49,…
第2問
あるきまりにしたがって、数が並んでいます。□にあてはまる数を答えなさい。
(1)1,5,9,13,17,□,25,…
(2)1,3,9,27,81,□,729,…
(3)1,3,6,10,15,□,28,…
(4)1,4,9,16,25,□,49,…
【受験算数】下のように、あるきまりにしたがって左から順に数が並んでいます。20番目の数は何ですか。1,2,4,7,11,16,22,29,…

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
第1問 下のように、あるきまりにしたがって左から順に数が並んでいます。20番目の数は何ですか。
1,2,4,7,11,16,22,29,…
第2問 下のように、あるきまりにしたがって左から順に数が並んでいます。25番目の数は何ですか。
1,2,6,13,23,36,52,71,…
この動画を見る
第1問 下のように、あるきまりにしたがって左から順に数が並んでいます。20番目の数は何ですか。
1,2,4,7,11,16,22,29,…
第2問 下のように、あるきまりにしたがって左から順に数が並んでいます。25番目の数は何ですか。
1,2,6,13,23,36,52,71,…
