 センター試験・共通テスト関連
センター試験・共通テスト関連
 センター試験・共通テスト関連
センター試験・共通テスト関連
【残り9日】共テ数学IAの全大問解説、まとめました【流し見OK】

単元:
#大学入試過去問(数学)#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
共通テスト数学IAの全大問解説、まとめ動画です
この動画を見る
共通テスト数学IAの全大問解説、まとめ動画です
共通テストでめちゃ使えるベクトルの裏技(s, t問題)(公式)

単元:
#大学入試過去問(数学)#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#センター試験・共通テスト関連#共通テスト#数学(高校生)#数C
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
共通テストで使えるベクトルの裏技説明動画です(s, t問題)
この動画を見る
共通テストで使えるベクトルの裏技説明動画です(s, t問題)
5年連続的中!共通テスト2024出題予想~問題流出同然の「今年はコレが出る」一覧

単元:
#大学入試過去問(数学)#化学#生物#センター試験・共通テスト関連#共通テスト#大学入試過去問(化学)#英語(高校生)#国語(高校生)#社会(高校生)#日本史#世界史#大学入試過去問(英語)#大学入試過去問(国語)#共通テスト#共通テスト(現代文)#大学入試過去問(生物)#共通テスト・センター試験#共通テスト(古文)#共通テスト#大学入試過去問・共通テスト・模試関連#大学入試過去問・共通テスト・模試関連#数学(高校生)#理科(高校生)
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
共通テスト2024の出題予想です。
この動画では私、篠原が過去の問題の傾向から、2024年の共通テストの問題を予想します。
英語・数学・国語・理科・社会に分けて、出題予想、対策方法を紹介しています。
受験生のみなさん、合格目指してラストスパート頑張りましょう!
#共通テスト
#出題予想
#受験生
#共通テスト2024予想
#篠原好
#京都大学
#勉強法
#大学受験
#受験勉強
#大学入試
この動画を見る
共通テスト2024の出題予想です。
この動画では私、篠原が過去の問題の傾向から、2024年の共通テストの問題を予想します。
英語・数学・国語・理科・社会に分けて、出題予想、対策方法を紹介しています。
受験生のみなさん、合格目指してラストスパート頑張りましょう!
#共通テスト
#出題予想
#受験生
#共通テスト2024予想
#篠原好
#京都大学
#勉強法
#大学受験
#受験勉強
#大学入試
【共テ数学IIB】知らなきゃ損な裏技集__これで解答時間をキュッと短縮します(指数・対数、微分積分、数列、ベクトル)

単元:
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#指数関数と対数関数#微分法と積分法#指数関数#対数関数#数列#数列とその和(等差・等比・階差・Σ)#センター試験・共通テスト関連#共通テスト#数学(高校生)#数B#数C
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
【共テ数学IIB】解答時間短縮裏技集 紹介動画です(指数・対数、微分積分、数列、ベクトル)
この動画を見る
【共テ数学IIB】解答時間短縮裏技集 紹介動画です(指数・対数、微分積分、数列、ベクトル)
【共テ数学IIB】知らなきゃ損な裏技集__これで解答時間をキュッと短縮します(指数・対数、微分積分、数列、ベクトル)

単元:
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#指数関数と対数関数#微分法と積分法#指数関数#対数関数#数列#センター試験・共通テスト関連#共通テスト#数学(高校生)#数B#数C
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
【共テ数学IIB】解答時間短縮、裏技集説明動画です。(指数・対数、微分積分、数列、ベクトル)
この動画を見る
【共テ数学IIB】解答時間短縮、裏技集説明動画です。(指数・対数、微分積分、数列、ベクトル)
【共通テスト】数学IA 第3問確率がめっちゃ簡単になる本質テクニック、教えます(2023年本試)

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
【共通テスト】数学IA 第3問確率が簡単になるテクニック、解説動画です
球が4つある。
赤、青、黄、緑、紫のうちいずれか1色でそれぞれ塗る。
1本の紐で繋がれた2つの球は異なる色。
赤をちょうど2回使う塗り方は何通り?
この動画を見る
【共通テスト】数学IA 第3問確率が簡単になるテクニック、解説動画です
球が4つある。
赤、青、黄、緑、紫のうちいずれか1色でそれぞれ塗る。
1本の紐で繋がれた2つの球は異なる色。
赤をちょうど2回使う塗り方は何通り?
【共通テスト】数学IA 第2問でスラスラ解けるテクニック、解説します(2023年本試)

単元:
#数Ⅰ#大学入試過去問(数学)#データの分析#データの分析#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
【共通テスト】数学IA 第2問で解けるテクニック、解説動画です
この動画を見る
【共通テスト】数学IA 第2問で解けるテクニック、解説動画です
【共通テスト】数学IA 第1問で満点取る思考回路、解説します(2023年本試)

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#図形と計量#一次不等式(不等式・絶対値のある方程式・不等式)#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
【共通テスト】数学IA 第1問で満点取る思考回路、解説
(1)
実数$x$についての不等式$|x+6| \leqq 2$の解は[アイ]$ \leqq x \leqq $[ウエ]である。
よって実数$a,b,c,d$が$|(1-\sqrt{ 3 }(a-b)(c-d)+6|\leqq 2$を満たしているとき、
$1-\sqrt{ 3 }$は負であることに注意すると、$(a-b)(c-d)$のとり得る値の範囲は
[オ]+[カ]$\sqrt{ 3 } \leqq (a-b)(c-d) \leqq$[キ]+[ク]$\sqrt{ 3 }$であることがわかる。
$(a-b)(c-d)=$[キ]+[ク]$\sqrt{ 3 }$・・・・①
であるとき、さらに
$(a-b)(c-d)=-3+\sqrt{ 3 }$・・・・②
が成り立つならば
$(a-b)(c-d)=$[ケ]+[コ]$\sqrt{ 3 }$・・・・③
であることが、等式①、②、③の左辺を展開して比較することによりわかる。
(2)
点Oを中心とし、半径が5である円0がある。
この円周上に2点A,BをAB=6となるようにとる。
また、円Oの円周上に、2点A,Bとは異なる点Cをとる。
①$\sin \angle ACB =$[サ]である。また、点Cを$\angle ACB$が純角となるようにとるとき、$\cos \angle ACB =$[シ]である。
②点Cを$\triangle ABC$の面積が最大となるようにとる。点Cから直角ABに垂直な直線を引き、直線ABとの交点をDとするとき、$\tan \angle OAD =$[ス]である。
また、$\triangle ABC$の面積は[セソ]である。
この動画を見る
【共通テスト】数学IA 第1問で満点取る思考回路、解説
(1)
実数$x$についての不等式$|x+6| \leqq 2$の解は[アイ]$ \leqq x \leqq $[ウエ]である。
よって実数$a,b,c,d$が$|(1-\sqrt{ 3 }(a-b)(c-d)+6|\leqq 2$を満たしているとき、
$1-\sqrt{ 3 }$は負であることに注意すると、$(a-b)(c-d)$のとり得る値の範囲は
[オ]+[カ]$\sqrt{ 3 } \leqq (a-b)(c-d) \leqq$[キ]+[ク]$\sqrt{ 3 }$であることがわかる。
$(a-b)(c-d)=$[キ]+[ク]$\sqrt{ 3 }$・・・・①
であるとき、さらに
$(a-b)(c-d)=-3+\sqrt{ 3 }$・・・・②
が成り立つならば
$(a-b)(c-d)=$[ケ]+[コ]$\sqrt{ 3 }$・・・・③
であることが、等式①、②、③の左辺を展開して比較することによりわかる。
(2)
点Oを中心とし、半径が5である円0がある。
この円周上に2点A,BをAB=6となるようにとる。
また、円Oの円周上に、2点A,Bとは異なる点Cをとる。
①$\sin \angle ACB =$[サ]である。また、点Cを$\angle ACB$が純角となるようにとるとき、$\cos \angle ACB =$[シ]である。
②点Cを$\triangle ABC$の面積が最大となるようにとる。点Cから直角ABに垂直な直線を引き、直線ABとの交点をDとするとき、$\tan \angle OAD =$[ス]である。
また、$\triangle ABC$の面積は[セソ]である。
【共通テスト本番】数学2Bのテクニック5選

単元:
#大学入試過去問(数学)#センター試験・共通テスト関連#共通テスト#その他#勉強法#数学(高校生)
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
数学2Bのテクニック5選
この動画を見る
数学2Bのテクニック5選
【共通テスト本番】数学1Aのテクニック5選

単元:
#大学入試過去問(数学)#センター試験・共通テスト関連#共通テスト#その他#勉強法#数学(高校生)
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
数学1Aのテクニック5選
この動画を見る
数学1Aのテクニック5選
【篠原共通塾】2021年度「数学1A」共通テスト過去問解説

単元:
#大学入試過去問(数学)#センター試験・共通テスト関連#共通テスト#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
2021年度「数学1A」共通テスト過去問解説です。
この動画を見る
2021年度「数学1A」共通テスト過去問解説です。
【篠原共通塾】2021年度「数学2B」共通テスト過去問解説

単元:
#大学入試過去問(数学)#センター試験・共通テスト関連#共通テスト#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
2021年度共通テスト「数学2B」の解説動画です。
この動画を見る
2021年度共通テスト「数学2B」の解説動画です。
戦う準備はできているか。共通テストまで残り40日

単元:
#化学#生物#情報Ⅰ(高校生)#センター試験・共通テスト関連#共通テスト#英語(高校生)#国語(高校生)#社会(高校生)#世界史#共通テスト#共通テスト(現代文)#共通テスト・センター試験#共通テスト(古文)#共通テスト#大学入試過去問・共通テスト・模試関連#大学入試過去問・共通テスト・模試関連#数学(高校生)#理科(高校生)#数学#共通テスト#英語#化学#物理#共通テスト#共通テスト#共通テスト#共通テスト#【河合塾】全統共通テスト模試
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
共通テストまで40日。点数アップのための方法解説動画です
この動画を見る
共通テストまで40日。点数アップのための方法解説動画です
【篠原共通塾】2022年度「数学2B」共通テスト過去問解説

単元:
#大学入試過去問(数学)#センター試験・共通テスト関連#共通テスト#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
2022年度共通テスト「数学2B」の解説動画です。
この動画を見る
2022年度共通テスト「数学2B」の解説動画です。
【篠原共通塾】2022年度「数学1A」共通テスト過去問解説

単元:
#大学入試過去問(数学)#センター試験・共通テスト関連#共通テスト#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
2022年度共通テスト「数学1A」の解説動画
この動画を見る
2022年度共通テスト「数学1A」の解説動画
【12月勉強】この優先順位で勉強すると伸びます。

単元:
#大学入試過去問(数学)#物理#化学#生物#センター試験・共通テスト関連#共通テスト#その他#大学入試過去問(物理)#大学入試過去問(化学)#英語(高校生)#国語(高校生)#社会(高校生)#日本史#世界史#勉強法・その他#大学入試過去問(英語)#大学入試過去問(国語)#共通テスト#共通テスト(現代文)#勉強法#勉強法#その他#大学入試過去問(生物)#共通テスト・センター試験#共通テスト(古文)#共通テスト#勉強法#大学入試過去問・共通テスト・模試関連#大学入試過去問・共通テスト・模試関連#数学(高校生)#理科(高校生)#大学入試解答速報#数学#共通テスト#英語#化学#物理#共通テスト#共通テスト#共通テスト#共通テスト#世界史#共通テスト
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
12月の勉強法 優先順位説明動画です
この動画を見る
12月の勉強法 優先順位説明動画です
福田の数学〜共通テスト対策にもってこい〜明治大学2023年全学部統一ⅠⅡAB第3問〜四面体の体積
単元:
#数A#大学入試過去問(数学)#図形の性質#センター試験・共通テスト関連#学校別大学入試過去問解説(数学)#共通テスト#空間における垂直と平行と多面体(オイラーの法則)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
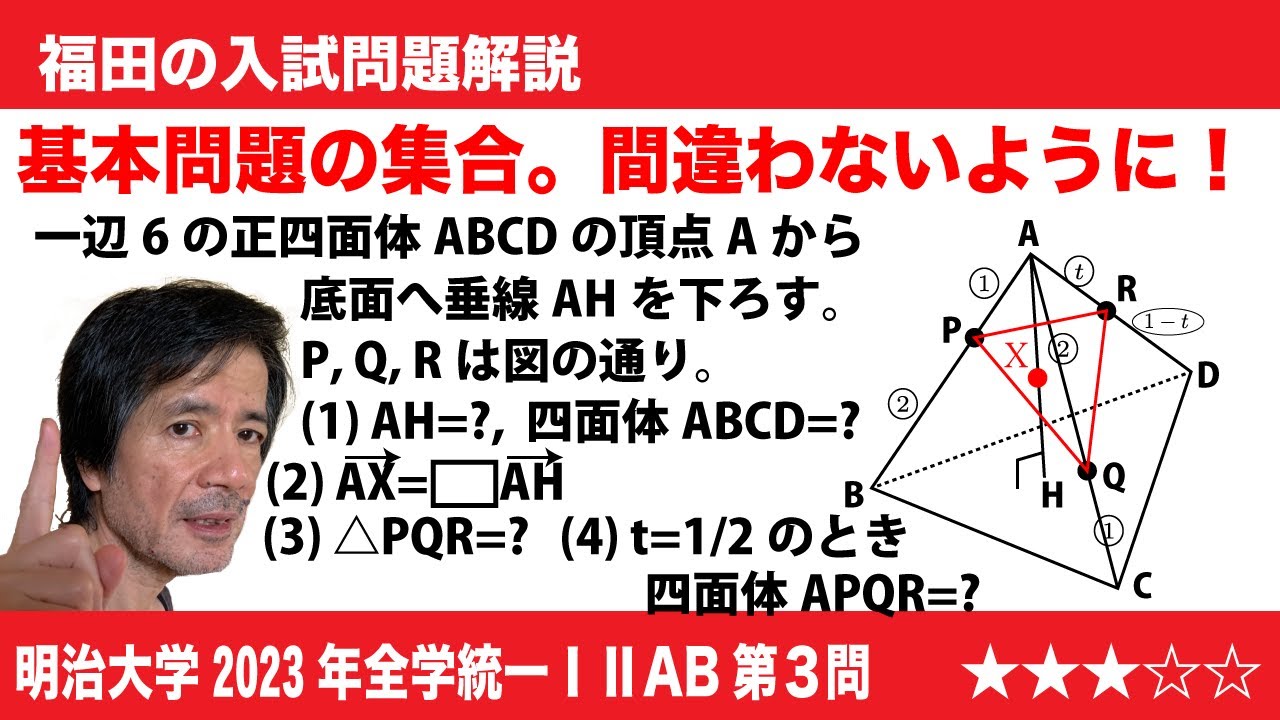
$\Large{\boxed{3}}$ 一辺の長さが6の正四面体ABCDにおいて、点Aから3点B,C,Dを含む平面に垂線AHを下ろす。また、辺ABを1:2に内分する点をP、辺ACを2:1に内分する点をQ、辺ADを$t$:1-$t$に内分する点をRとする。ただし、
0<$t$<1 とする。
(1)AHの長さは$\boxed{\ \ ア\ \ }\sqrt{\boxed{\ \ イ\ \ }}$ であり、正四面体ABCDの体積は$\boxed{\ \ ウエ\ \ }\sqrt{\boxed{\ \ オ\ \ }}$ である。
(2)AHと三角形PQRの交点をXとすると、$\overrightarrow{AX}$=$\boxed{\ \ カ\ \ }\overrightarrow{AH}$ である。
(3)三角形PQRの面積は$\sqrt{\boxed{\ \ キク\ \ }t^2-\boxed{\ \ ケコ\ \ }t+\boxed{\ \ サシ\ \ }}$ である。
(4)$t$=$\frac{1}{2}$ のとき、四面体APQRの体積は$\boxed{\ \ ス\ \ }\sqrt{\boxed{\ \ セ\ \ }}$で、点Aから3点P,Q,Rを通る平面に垂線AYを下ろすと、AYの長さは$\frac{\boxed{\ \ ソ\ \ }\sqrt{\boxed{\ \ タ\ \ }}}{\boxed{\ \ チ\ \ }}$ である。
この動画を見る
$\Large{\boxed{3}}$ 一辺の長さが6の正四面体ABCDにおいて、点Aから3点B,C,Dを含む平面に垂線AHを下ろす。また、辺ABを1:2に内分する点をP、辺ACを2:1に内分する点をQ、辺ADを$t$:1-$t$に内分する点をRとする。ただし、
0<$t$<1 とする。
(1)AHの長さは$\boxed{\ \ ア\ \ }\sqrt{\boxed{\ \ イ\ \ }}$ であり、正四面体ABCDの体積は$\boxed{\ \ ウエ\ \ }\sqrt{\boxed{\ \ オ\ \ }}$ である。
(2)AHと三角形PQRの交点をXとすると、$\overrightarrow{AX}$=$\boxed{\ \ カ\ \ }\overrightarrow{AH}$ である。
(3)三角形PQRの面積は$\sqrt{\boxed{\ \ キク\ \ }t^2-\boxed{\ \ ケコ\ \ }t+\boxed{\ \ サシ\ \ }}$ である。
(4)$t$=$\frac{1}{2}$ のとき、四面体APQRの体積は$\boxed{\ \ ス\ \ }\sqrt{\boxed{\ \ セ\ \ }}$で、点Aから3点P,Q,Rを通る平面に垂線AYを下ろすと、AYの長さは$\frac{\boxed{\ \ ソ\ \ }\sqrt{\boxed{\ \ タ\ \ }}}{\boxed{\ \ チ\ \ }}$ である。
共通テストまで、あと90日。受験生がやるべきこと3選。

単元:
#大学入試過去問(数学)#物理#化学#生物#センター試験・共通テスト関連#共通テスト#大学入試過去問(物理)#大学入試過去問(化学)#英語(高校生)#国語(高校生)#社会(高校生)#日本史#世界史#大学入試過去問(英語)#大学入試過去問(国語)#共通テスト#共通テスト(現代文)#その他#大学入試過去問(生物)#共通テスト・センター試験#共通テスト(古文)#共通テスト#勉強法#大学入試過去問・共通テスト・模試関連#大学入試過去問・共通テスト・模試関連#数学(高校生)#理科(高校生)#共通テスト
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
共通テストまで、あと90日。受験生がやるべきこと3選。
この動画を見る
共通テストまで、あと90日。受験生がやるべきこと3選。
数学IIB、〇〇ができれば「50点」<共通テスト>

単元:
#センター試験・共通テスト関連#共通テスト#数学(高校生)#数B
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
数学IIB、最短で50点獲得する勉強法紹介動画です
この動画を見る
数学IIB、最短で50点獲得する勉強法紹介動画です
【共通テスト】数IAを最短で50点にする方法はこれです。

単元:
#センター試験・共通テスト関連#共通テスト#その他#勉強法#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
【共通テスト】数IAを最短で50点にする方法紹介動画です
この動画を見る
【共通テスト】数IAを最短で50点にする方法紹介動画です
福田の数学〜2023年共通テスト速報〜数学IIB第3問確率分布〜正規分布と二項分布

単元:
#大学入試過去問(数学)#確率分布と統計的な推測#確率分布#センター試験・共通テスト関連#共通テスト#数学(高校生)#大学入試解答速報#数学#共通テスト#数B
指導講師:
福田次郎
問題文全文(内容文):
第3問
以下の問題を解答するにあたっては、必要に応じて43ページの正規分布表を用いてもよい。
(1)ある生産地で生産されるピーマン全体を母集団とし、この母集団におけるピーマン1個の重さ(単位はg)を表す確率変数をXとする。mとσを正の実数とし、Xは正規分布N(m, $\sigma^2$)に従うとする。
(i)この母集団から1個のピーマンを無作為に抽出したとき、重さがm g以上である確率P(X≧m)は
P(X≧m)=P$\left(\frac{X-m}{\sigma}\geqq \boxed{\ \ ア\ \ }\right)$=$\frac{\boxed{\ \ イ\ \ }}{\boxed{\ \ ウ\ \ }}$
である。
(ii)母集団から無作為に抽出された大きさnの標本$X_1$, $X_2$, ..., $X_n$の標本平均を$\bar{X}$とする。$\bar{X}$の平均(期待値)と標準偏差はそれぞれ
E($\bar{X}$)=$\boxed{\boxed{\ \ エ\ \ }}$, σ($\bar{X}$)=$\boxed{\boxed{\ \ オ\ \ }}$
となる。
n=400, 標本平均が30.0g, 標本の標準偏差が3.6gのとき、mの信頼度90%の信頼区間を次の方針で求めよう。
方針:Zを標準正規分布N(0,1)に従う確率変数として、P($-z_0 \leqq Z \leqq z_0$)=0.901 となる$z_0$を正規分布表から求める。この$z_0$を用いるとmの信頼度90.1%の信頼区間が求められるが、これを信頼度90%の信頼区間とみなして考える。
方針において、$z_0$=$\boxed{\ \ カ\ \ }$.$\boxed{\ \ キク\ \ }$である。
一般に、標本の大きさnが大きいときには、母標準偏差の代わりに、標本の標準偏差を用いてよいことが知られている。n=400は十分に大きいので、方針に基づくと、mの信頼度90%の信頼区間は$\boxed{\boxed{\ \ ケ\ \ }}$となる。
$\boxed{\boxed{\ \ エ\ \ }}, \boxed{\boxed{\ \ オ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪σ ①$\sigma^2$ ②$\frac{\sigma}{\sqrt n}$ ③$\frac{\sigma^2}{n}$
④m ⑤2m ⑥$m^2$ ⑦$\sqrt m$
⑧$\frac{\sigma}{n}$ ⑨$n\sigma $ⓐ$nm$ ⓑ$\frac{m}{n}$
$\boxed{\boxed{\ \ ケ\ \ }}$については、最も適当なものを、次の⓪~⑤のうちから一つ選べ。
⓪28.6≦m≦31.4 ①28.7≦m≦31.3 ②28.9≦m≦31.1
③29.6≦m≦30.4 ④29.7≦m≦30.3 ⑤29.9≦m≦30.1
(2)(1)の確率変数Xにおいて、m=30.0, σ=3.6とした母集団から無作為にピーマンを1個ずつ抽出し、ピーマン2個を1組にしたものを袋に入れていく。このようにしてピーマン2個を1組にしたものを25袋作る。その際、1袋ずつの重さの分数を小さくするために、次のピーマン分類法を考える。
ピーマン分類法:無作為に抽出したいくつかのピーマンについて、重さが30.0g以下のときをSサイズ、30.0gを超えるときはLサイズと分類する。そして、分類されたピーマンからSサイズとLサイズのピーマンを一つずつ選び、ピーマン2個を1組とした袋を作る。
(i)ピーマンを無作為に50個抽出した時、ピーマン分類法で25袋作ることができる確率$p_0$を考えよう。無作為に1個抽出したピーマンがSサイズである確率は$\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}$である。ピーマンを無作為に50個抽出したときのSサイズのピーマンの個数を表す確率変数を$U_0$とすると、$U_0$は二項分布$B\left(50, \frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\right)$に従うので
$p_0$=${}_{50}C_{\boxed{シス}}×\left(\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\right)^{\boxed{シス}}×\left(1-\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\right)^{50-\boxed{シス}}$
となる。
$p_0$を計算すると、$p_0$=0.1122...となることから、ピーマンを無作為に50個抽出したとき、25袋作ることができる確率は0.11程度とわかる。
(ii)ピーマン分類法で25袋作ることができる確率が0.95以上となるようなピーマンの個数を考えよう。
kを自然数とし、ピーマンを無作為に(50+k)個抽出したとき、Sサイズのピーマンの個数を表す確率変数を$U_k$とすると、$U_k$は二項分布$B\left(50+k, \frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\right)$に従う。
(50+k)は十分に大きいので、$U_k$は近似的に正規分布$N\left(\boxed{\boxed{\ \ セ\ \ }}, \boxed{\boxed{\ \ ソ\ \ }}\right)$に従い、$Y=\frac{U_k-\boxed{\boxed{\ \ セ\ \ }}}{\sqrt{\boxed{\boxed{\ \ ソ\ \ }}}}$とすると、Yは近似的に標準正規分布N(0,1)に従う。
よって、ピーマン分類法で、25袋作ることができる確率を$p_k$とすると
$p_k$=$P(25 \leqq U_k \leqq 25+k)$=$P\left(-\frac{\boxed{\boxed{\ \ タ\ \ }}}{\sqrt{50+k}} \leqq Y \leqq \frac{\boxed{\boxed{\ \ タ\ \ }}}{\sqrt{50+k}}\right)$
となる。
$\boxed{\boxed{\ \ タ\ \ }}$=a, $\sqrt{50+k}$=$\beta$とおく。
$p_k$≧0.95になるような$\frac{\alpha}{\beta}$について、正規分布表から$\frac{\alpha}{\beta}$≧1.96を満たせばよいことが分かる。ここでは
$\frac{\alpha}{\beta}$≧2 ...①
を満たす自然数kを考えることとする。①の両辺は正であるから、$\alpha^2$≧4$\beta^2$を満たす最小のkを$k_0$とすると、$k_0$=$\boxed{\ \ チツ\ \ }$であることがわかる。ただし、$\boxed{\ \ チツ\ \ }$の計算においては、$\sqrt{51}=7.14$を用いてもよい。
したがって、少なくとも(50+$\boxed{\ \ チツ\ \ }$)個のピーマンを抽出しておけば、ピーマン分類法で25袋作ることができる確率は0.95以上となる。
$\boxed{\boxed{\ \ セ\ \ }}$~$\boxed{\boxed{\ \ タ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪k ①2k ②3k ③$\frac{50+k}{2}$
④$\frac{25+k}{2}$ ⑤25+k ⑥$\frac{\sqrt{50+k}}{2}$ ⑦$\frac{50+k}{4}$
2023共通テスト過去問
この動画を見る
第3問
以下の問題を解答するにあたっては、必要に応じて43ページの正規分布表を用いてもよい。
(1)ある生産地で生産されるピーマン全体を母集団とし、この母集団におけるピーマン1個の重さ(単位はg)を表す確率変数をXとする。mとσを正の実数とし、Xは正規分布N(m, $\sigma^2$)に従うとする。
(i)この母集団から1個のピーマンを無作為に抽出したとき、重さがm g以上である確率P(X≧m)は
P(X≧m)=P$\left(\frac{X-m}{\sigma}\geqq \boxed{\ \ ア\ \ }\right)$=$\frac{\boxed{\ \ イ\ \ }}{\boxed{\ \ ウ\ \ }}$
である。
(ii)母集団から無作為に抽出された大きさnの標本$X_1$, $X_2$, ..., $X_n$の標本平均を$\bar{X}$とする。$\bar{X}$の平均(期待値)と標準偏差はそれぞれ
E($\bar{X}$)=$\boxed{\boxed{\ \ エ\ \ }}$, σ($\bar{X}$)=$\boxed{\boxed{\ \ オ\ \ }}$
となる。
n=400, 標本平均が30.0g, 標本の標準偏差が3.6gのとき、mの信頼度90%の信頼区間を次の方針で求めよう。
方針:Zを標準正規分布N(0,1)に従う確率変数として、P($-z_0 \leqq Z \leqq z_0$)=0.901 となる$z_0$を正規分布表から求める。この$z_0$を用いるとmの信頼度90.1%の信頼区間が求められるが、これを信頼度90%の信頼区間とみなして考える。
方針において、$z_0$=$\boxed{\ \ カ\ \ }$.$\boxed{\ \ キク\ \ }$である。
一般に、標本の大きさnが大きいときには、母標準偏差の代わりに、標本の標準偏差を用いてよいことが知られている。n=400は十分に大きいので、方針に基づくと、mの信頼度90%の信頼区間は$\boxed{\boxed{\ \ ケ\ \ }}$となる。
$\boxed{\boxed{\ \ エ\ \ }}, \boxed{\boxed{\ \ オ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪σ ①$\sigma^2$ ②$\frac{\sigma}{\sqrt n}$ ③$\frac{\sigma^2}{n}$
④m ⑤2m ⑥$m^2$ ⑦$\sqrt m$
⑧$\frac{\sigma}{n}$ ⑨$n\sigma $ⓐ$nm$ ⓑ$\frac{m}{n}$
$\boxed{\boxed{\ \ ケ\ \ }}$については、最も適当なものを、次の⓪~⑤のうちから一つ選べ。
⓪28.6≦m≦31.4 ①28.7≦m≦31.3 ②28.9≦m≦31.1
③29.6≦m≦30.4 ④29.7≦m≦30.3 ⑤29.9≦m≦30.1
(2)(1)の確率変数Xにおいて、m=30.0, σ=3.6とした母集団から無作為にピーマンを1個ずつ抽出し、ピーマン2個を1組にしたものを袋に入れていく。このようにしてピーマン2個を1組にしたものを25袋作る。その際、1袋ずつの重さの分数を小さくするために、次のピーマン分類法を考える。
ピーマン分類法:無作為に抽出したいくつかのピーマンについて、重さが30.0g以下のときをSサイズ、30.0gを超えるときはLサイズと分類する。そして、分類されたピーマンからSサイズとLサイズのピーマンを一つずつ選び、ピーマン2個を1組とした袋を作る。
(i)ピーマンを無作為に50個抽出した時、ピーマン分類法で25袋作ることができる確率$p_0$を考えよう。無作為に1個抽出したピーマンがSサイズである確率は$\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}$である。ピーマンを無作為に50個抽出したときのSサイズのピーマンの個数を表す確率変数を$U_0$とすると、$U_0$は二項分布$B\left(50, \frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\right)$に従うので
$p_0$=${}_{50}C_{\boxed{シス}}×\left(\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\right)^{\boxed{シス}}×\left(1-\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\right)^{50-\boxed{シス}}$
となる。
$p_0$を計算すると、$p_0$=0.1122...となることから、ピーマンを無作為に50個抽出したとき、25袋作ることができる確率は0.11程度とわかる。
(ii)ピーマン分類法で25袋作ることができる確率が0.95以上となるようなピーマンの個数を考えよう。
kを自然数とし、ピーマンを無作為に(50+k)個抽出したとき、Sサイズのピーマンの個数を表す確率変数を$U_k$とすると、$U_k$は二項分布$B\left(50+k, \frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\right)$に従う。
(50+k)は十分に大きいので、$U_k$は近似的に正規分布$N\left(\boxed{\boxed{\ \ セ\ \ }}, \boxed{\boxed{\ \ ソ\ \ }}\right)$に従い、$Y=\frac{U_k-\boxed{\boxed{\ \ セ\ \ }}}{\sqrt{\boxed{\boxed{\ \ ソ\ \ }}}}$とすると、Yは近似的に標準正規分布N(0,1)に従う。
よって、ピーマン分類法で、25袋作ることができる確率を$p_k$とすると
$p_k$=$P(25 \leqq U_k \leqq 25+k)$=$P\left(-\frac{\boxed{\boxed{\ \ タ\ \ }}}{\sqrt{50+k}} \leqq Y \leqq \frac{\boxed{\boxed{\ \ タ\ \ }}}{\sqrt{50+k}}\right)$
となる。
$\boxed{\boxed{\ \ タ\ \ }}$=a, $\sqrt{50+k}$=$\beta$とおく。
$p_k$≧0.95になるような$\frac{\alpha}{\beta}$について、正規分布表から$\frac{\alpha}{\beta}$≧1.96を満たせばよいことが分かる。ここでは
$\frac{\alpha}{\beta}$≧2 ...①
を満たす自然数kを考えることとする。①の両辺は正であるから、$\alpha^2$≧4$\beta^2$を満たす最小のkを$k_0$とすると、$k_0$=$\boxed{\ \ チツ\ \ }$であることがわかる。ただし、$\boxed{\ \ チツ\ \ }$の計算においては、$\sqrt{51}=7.14$を用いてもよい。
したがって、少なくとも(50+$\boxed{\ \ チツ\ \ }$)個のピーマンを抽出しておけば、ピーマン分類法で25袋作ることができる確率は0.95以上となる。
$\boxed{\boxed{\ \ セ\ \ }}$~$\boxed{\boxed{\ \ タ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪k ①2k ②3k ③$\frac{50+k}{2}$
④$\frac{25+k}{2}$ ⑤25+k ⑥$\frac{\sqrt{50+k}}{2}$ ⑦$\frac{50+k}{4}$
2023共通テスト過去問
福田の数学〜2023年共通テスト速報〜数学IIB第5問ベクトル〜三角錐をベクトルで考える

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#センター試験・共通テスト関連#共通テスト#数学(高校生)#大学入試解答速報#数学#共通テスト#数C
指導講師:
福田次郎
問題文全文(内容文):
第5問
三角錐PABCにおいて、辺BCの中点をMとおく。また、$\angle$PAB=$\angle$PACとし、この角度をθをおく。0°< θ < 90°とする。
(1)$\overrightarrow{AM}$は
$\overrightarrow{AM}$=$\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}\overrightarrow{AB}$+$\frac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ エ\ \ }}\overrightarrow{AC}$
と表せる。また
$\frac{\overrightarrow{AP}・\overrightarrow{AB}}{|\overrightarrow{AP}||\overrightarrow{AB}|}$=$\frac{\overrightarrow{AP}・\overrightarrow{AC}}{|\overrightarrow{AP}||\overrightarrow{AC}|}$=$\boxed{\boxed{\ \ オ\ \ }}$ ...①
$\boxed{\boxed{\ \ オ\ \ }}$の解答群
⓪$\sin \theta$ ①$\cos \theta$ ②$\tan \theta$
③$\frac{1}{\sin \theta}$ ④$\frac{1}{\cos \theta}$ ⑤$\frac{1}{\tan \theta}$
⑥$\sin\angle$BPC ⑦$\cos\angle$BPC ⑧$\tan\angle$BPC
(2)θ=45°とし、さらに
$|\overrightarrow{AP}|$=3√2, $|\overrightarrow{AB}|$=$|\overrightarrow{PB}|$=3, $|\overrightarrow{AC}|$=$|\overrightarrow{PC}|$=3
が成り立つ場合を考える。このとき
$\overrightarrow{AP}・\overrightarrow{AB}$=$\overrightarrow{AP}・\overrightarrow{AC}$=$\boxed{\ \ カ\ \ }$
である。さらに、直線AM上の点Dが$\angle$APD=90°を満たしているとする。このとき、$\overrightarrow{AD}$=$\boxed{\ \ キ\ \ }\overrightarrow{AM}$である。
(3)
$\overrightarrow{AQ}$=$\boxed{\ \ キ\ \ }\overrightarrow{AM}$
で定まる点をQとおく。$\overrightarrow{PA}$と$\overrightarrow{PQ}$が垂直である三角錐PABCはどのようなものかについて考えよう。例えば(2)の場合では、点Qは点Dと一致し、$\overrightarrow{PA}$と$\overrightarrow{PQ}$は垂直である。
(i)$\overrightarrow{PA}$と$\overrightarrow{PQ}$が垂直であるとき、$\overrightarrow{PQ}$を$\overrightarrow{AB}$,$\overrightarrow{AC}$,$\overrightarrow{AP}$を用いて表して考えると、$\boxed{\boxed{\ \ ク\ \ }}$が成り立つ。さらに①に注意すると、$\boxed{\boxed{\ \ ク\ \ }}$から$\boxed{\boxed{\ \ ケ\ \ }}$が成り立つことがわかる。
したがって、$\overrightarrow{PA}$と$\overrightarrow{PQ}$が垂直であれば、$\boxed{\boxed{\ \ ケ\ \ }}$が成り立つ。逆に、$\boxed{\boxed{\ \ ケ\ \ }}$が成り立てば、$\overrightarrow{PA}$と$\overrightarrow{PQ}$は垂直である。
$\boxed{\boxed{\ \ ク\ \ }}$の解答群
⓪$\overrightarrow{AP}・\overrightarrow{AB}$+$\overrightarrow{AP}・\overrightarrow{AC}$=$\overrightarrow{AP}・\overrightarrow{AP}$
①$\overrightarrow{AP}・\overrightarrow{AB}$+$\overrightarrow{AP}・\overrightarrow{AC}$=$-\overrightarrow{AP}・\overrightarrow{AP}$
②$\overrightarrow{AP}・\overrightarrow{AB}$+$\overrightarrow{AP}・\overrightarrow{AC}$=$\overrightarrow{AB}・\overrightarrow{AC}$
③$\overrightarrow{AP}・\overrightarrow{AB}$+$\overrightarrow{AP}・\overrightarrow{AC}$=$-\overrightarrow{AB}・\overrightarrow{AC}$
④$\overrightarrow{AP}・\overrightarrow{AB}$+$\overrightarrow{AP}・\overrightarrow{AC}$=0
⑤$\overrightarrow{AP}・\overrightarrow{AB}$-$\overrightarrow{AP}・\overrightarrow{AC}$=0
$\boxed{\boxed{\ \ ケ\ \ }}$の解答群
⓪$|\overrightarrow{AB}|$+$|\overrightarrow{AC}|$=$\sqrt 2|\overrightarrow{BC}|$
①$|\overrightarrow{AB}|$+$|\overrightarrow{AC}|$=$2|\overrightarrow{BC}|$
②$|\overrightarrow{AB}|\sin\theta$+$|\overrightarrow{AC}|\sin\theta$=$|\overrightarrow{AP}|$
③$|\overrightarrow{AB}|\cos\theta$+$|\overrightarrow{AC}|\cos\theta$=$|\overrightarrow{AP}|$
④$|\overrightarrow{AB}|\sin\theta$=$|\overrightarrow{AC}|\sin\theta$=$2|\overrightarrow{AP}|$
⑤$|\overrightarrow{AB}|\cos\theta$=$|\overrightarrow{AC}|\cos\theta$=$2|\overrightarrow{AP}|$
(ii)kを正の実数とし
$k\overrightarrow{AP}・\overrightarrow{AB}$=$\overrightarrow{AP}・\overrightarrow{AC}$
が成り立つとする。このとき、$\boxed{\boxed{\ \ コ\ \ }}$が成り立つ。
また、点Bから直線APに下ろした垂線と直線APとの交点をB'とし、同様に点Cから直線APに下ろした垂線と直線APとの交点をC'とする。
このとき、$\overrightarrow{PA}$と$\overrightarrow{PQ}$が垂直であることは、$\boxed{\boxed{\ \ サ\ \ }}$であることと同値である。特にk=1のとき、$\overrightarrow{PA}$と$\overrightarrow{PQ}$が垂直であることは、$\boxed{\boxed{\ \ シ\ \ }}$であることと同値である。
$\boxed{\boxed{\ \ コ\ \ }}$の解答群
⓪$k|\overrightarrow{AB}|$=$|\overrightarrow{AC}|$ ①$|\overrightarrow{AB}|$=$k|\overrightarrow{AC}|$
②$k|\overrightarrow{AP}|$=$\sqrt 2|\overrightarrow{AB}|$ ③$k|\overrightarrow{AP}|$=$\sqrt 2|\overrightarrow{AC}|$
$\boxed{\boxed{\ \ サ\ \ }}$の解答群
⓪B'とC'がともに線分APの中点
①B'とC'が線分APをそれぞれ(k+1):1と1:(k+1)に内分する点
②B'とC'が線分APをそれぞれ1:(k+1)と(k+1):1に内分する点
③B'とC'が線分APをそれぞれk:1と1:kに内分する点
④B'とC'が線分APをそれぞれ1:kとk:1に内分する点
⑤B'とC'がともに線分APをk:1に内分する点
⑥B'とC'がともに線分APを1:kに内分する点
$\boxed{\boxed{\ \ シ\ \ }}$の解答群
⓪$\triangle$PABと$\triangle$PACがともに正三角形
①$\triangle$PABと$\triangle$PACがそれぞれ$\angle$PBA=90°, $\angle$PCA=90°を満たす直角二等辺三角形
②$\triangle$PABと$\triangle$PACがそれぞれBP=BA, CP=CAを満たす二等辺三角形
③$\triangle$PABと$\triangle$PACが合同
④AP=BC
2023共通テスト過去問
この動画を見る
第5問
三角錐PABCにおいて、辺BCの中点をMとおく。また、$\angle$PAB=$\angle$PACとし、この角度をθをおく。0°< θ < 90°とする。
(1)$\overrightarrow{AM}$は
$\overrightarrow{AM}$=$\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}\overrightarrow{AB}$+$\frac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ エ\ \ }}\overrightarrow{AC}$
と表せる。また
$\frac{\overrightarrow{AP}・\overrightarrow{AB}}{|\overrightarrow{AP}||\overrightarrow{AB}|}$=$\frac{\overrightarrow{AP}・\overrightarrow{AC}}{|\overrightarrow{AP}||\overrightarrow{AC}|}$=$\boxed{\boxed{\ \ オ\ \ }}$ ...①
$\boxed{\boxed{\ \ オ\ \ }}$の解答群
⓪$\sin \theta$ ①$\cos \theta$ ②$\tan \theta$
③$\frac{1}{\sin \theta}$ ④$\frac{1}{\cos \theta}$ ⑤$\frac{1}{\tan \theta}$
⑥$\sin\angle$BPC ⑦$\cos\angle$BPC ⑧$\tan\angle$BPC
(2)θ=45°とし、さらに
$|\overrightarrow{AP}|$=3√2, $|\overrightarrow{AB}|$=$|\overrightarrow{PB}|$=3, $|\overrightarrow{AC}|$=$|\overrightarrow{PC}|$=3
が成り立つ場合を考える。このとき
$\overrightarrow{AP}・\overrightarrow{AB}$=$\overrightarrow{AP}・\overrightarrow{AC}$=$\boxed{\ \ カ\ \ }$
である。さらに、直線AM上の点Dが$\angle$APD=90°を満たしているとする。このとき、$\overrightarrow{AD}$=$\boxed{\ \ キ\ \ }\overrightarrow{AM}$である。
(3)
$\overrightarrow{AQ}$=$\boxed{\ \ キ\ \ }\overrightarrow{AM}$
で定まる点をQとおく。$\overrightarrow{PA}$と$\overrightarrow{PQ}$が垂直である三角錐PABCはどのようなものかについて考えよう。例えば(2)の場合では、点Qは点Dと一致し、$\overrightarrow{PA}$と$\overrightarrow{PQ}$は垂直である。
(i)$\overrightarrow{PA}$と$\overrightarrow{PQ}$が垂直であるとき、$\overrightarrow{PQ}$を$\overrightarrow{AB}$,$\overrightarrow{AC}$,$\overrightarrow{AP}$を用いて表して考えると、$\boxed{\boxed{\ \ ク\ \ }}$が成り立つ。さらに①に注意すると、$\boxed{\boxed{\ \ ク\ \ }}$から$\boxed{\boxed{\ \ ケ\ \ }}$が成り立つことがわかる。
したがって、$\overrightarrow{PA}$と$\overrightarrow{PQ}$が垂直であれば、$\boxed{\boxed{\ \ ケ\ \ }}$が成り立つ。逆に、$\boxed{\boxed{\ \ ケ\ \ }}$が成り立てば、$\overrightarrow{PA}$と$\overrightarrow{PQ}$は垂直である。
$\boxed{\boxed{\ \ ク\ \ }}$の解答群
⓪$\overrightarrow{AP}・\overrightarrow{AB}$+$\overrightarrow{AP}・\overrightarrow{AC}$=$\overrightarrow{AP}・\overrightarrow{AP}$
①$\overrightarrow{AP}・\overrightarrow{AB}$+$\overrightarrow{AP}・\overrightarrow{AC}$=$-\overrightarrow{AP}・\overrightarrow{AP}$
②$\overrightarrow{AP}・\overrightarrow{AB}$+$\overrightarrow{AP}・\overrightarrow{AC}$=$\overrightarrow{AB}・\overrightarrow{AC}$
③$\overrightarrow{AP}・\overrightarrow{AB}$+$\overrightarrow{AP}・\overrightarrow{AC}$=$-\overrightarrow{AB}・\overrightarrow{AC}$
④$\overrightarrow{AP}・\overrightarrow{AB}$+$\overrightarrow{AP}・\overrightarrow{AC}$=0
⑤$\overrightarrow{AP}・\overrightarrow{AB}$-$\overrightarrow{AP}・\overrightarrow{AC}$=0
$\boxed{\boxed{\ \ ケ\ \ }}$の解答群
⓪$|\overrightarrow{AB}|$+$|\overrightarrow{AC}|$=$\sqrt 2|\overrightarrow{BC}|$
①$|\overrightarrow{AB}|$+$|\overrightarrow{AC}|$=$2|\overrightarrow{BC}|$
②$|\overrightarrow{AB}|\sin\theta$+$|\overrightarrow{AC}|\sin\theta$=$|\overrightarrow{AP}|$
③$|\overrightarrow{AB}|\cos\theta$+$|\overrightarrow{AC}|\cos\theta$=$|\overrightarrow{AP}|$
④$|\overrightarrow{AB}|\sin\theta$=$|\overrightarrow{AC}|\sin\theta$=$2|\overrightarrow{AP}|$
⑤$|\overrightarrow{AB}|\cos\theta$=$|\overrightarrow{AC}|\cos\theta$=$2|\overrightarrow{AP}|$
(ii)kを正の実数とし
$k\overrightarrow{AP}・\overrightarrow{AB}$=$\overrightarrow{AP}・\overrightarrow{AC}$
が成り立つとする。このとき、$\boxed{\boxed{\ \ コ\ \ }}$が成り立つ。
また、点Bから直線APに下ろした垂線と直線APとの交点をB'とし、同様に点Cから直線APに下ろした垂線と直線APとの交点をC'とする。
このとき、$\overrightarrow{PA}$と$\overrightarrow{PQ}$が垂直であることは、$\boxed{\boxed{\ \ サ\ \ }}$であることと同値である。特にk=1のとき、$\overrightarrow{PA}$と$\overrightarrow{PQ}$が垂直であることは、$\boxed{\boxed{\ \ シ\ \ }}$であることと同値である。
$\boxed{\boxed{\ \ コ\ \ }}$の解答群
⓪$k|\overrightarrow{AB}|$=$|\overrightarrow{AC}|$ ①$|\overrightarrow{AB}|$=$k|\overrightarrow{AC}|$
②$k|\overrightarrow{AP}|$=$\sqrt 2|\overrightarrow{AB}|$ ③$k|\overrightarrow{AP}|$=$\sqrt 2|\overrightarrow{AC}|$
$\boxed{\boxed{\ \ サ\ \ }}$の解答群
⓪B'とC'がともに線分APの中点
①B'とC'が線分APをそれぞれ(k+1):1と1:(k+1)に内分する点
②B'とC'が線分APをそれぞれ1:(k+1)と(k+1):1に内分する点
③B'とC'が線分APをそれぞれk:1と1:kに内分する点
④B'とC'が線分APをそれぞれ1:kとk:1に内分する点
⑤B'とC'がともに線分APをk:1に内分する点
⑥B'とC'がともに線分APを1:kに内分する点
$\boxed{\boxed{\ \ シ\ \ }}$の解答群
⓪$\triangle$PABと$\triangle$PACがともに正三角形
①$\triangle$PABと$\triangle$PACがそれぞれ$\angle$PBA=90°, $\angle$PCA=90°を満たす直角二等辺三角形
②$\triangle$PABと$\triangle$PACがそれぞれBP=BA, CP=CAを満たす二等辺三角形
③$\triangle$PABと$\triangle$PACが合同
④AP=BC
2023共通テスト過去問
福田の数学〜2023年共通テスト速報〜数学IIB第1問三角関数と対数〜三角不等式と対数が有理数とならない条件

単元:
#数Ⅰ#数A#数Ⅱ#大学入試過去問(数学)#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#整数の性質#ユークリッド互除法と不定方程式・N進法#三角関数#指数関数と対数関数#三角関数とグラフ#指数関数#対数関数#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
第一問
[ 1 ] 三角関数の値の大小関係について考えよう。
(1) $x=\displaystyle\frac{\pi}{6}$のとき$\sin x\boxed{\boxed{\ \ ア\ \ }}\sin 2x$であり、$x=\frac{2}{3}\pi$のとき$\sin x\boxed{\boxed{\ \ イ\ \ }}\sin 2x$である。
$\boxed{\boxed{\ \ ア\ \ }}$, $\boxed{\boxed{\ \ イ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪< ①= ②>
(2) $\sin x$と$\sin 2x$の値の大小関係を詳しく調べよう。
$\sin 2x$-$\sin x$=$\sin 2x\left(\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ }\right)$
であるから、$\sin 2x$-$\sin x$>0が成り立つことは
「$\sin x$>0かつ $\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ } \gt 0$」... ①
「$\sin x$<0かつ $\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ } \lt 0$」... ②
が成り立つことと同値である。$0 \leqq x \leqq 2\pi$のとき、①が成り立つようなxの値の範囲は
$0 \lt x \lt \displaystyle\frac{\pi}{\boxed{\ \ オ\ \ }}$
であり、②が成り立つようなxの値の範囲は
$\pi \lt x \lt \displaystyle\frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ\ \ }}\pi$
である。よって、$0 \leqq x \leqq 2\pi$のとき、$\sin 2x \gt \sin x$が成り立つようなxの値の範囲は
$0 \lt x \lt \displaystyle\frac{\pi}{\boxed{\ \ オ\ \ }}, \pi \lt x \lt \displaystyle\frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ\ \ }}\pi$
である。
(3)$\sin 3x$と$\sin 4x$の値の大小関係を調べよう。
三角関数の加法定理を用いると、等式
$\sin(\alpha+\beta)$-$\sin(\alpha-\beta)$=$2\cos\alpha\sin\beta$...③
が得られる。$\alpha+\beta=4x$, $\alpha-\beta=3x$を満たす$\alpha$, $\beta$に対して③を用いることにより、$\sin 4x-\sin 3x \gt 0$が成り立つことは
「$\cos\boxed{\boxed{\ \ ク\ \ }} \gt 0$ かつ $\sin\boxed{\boxed{\ \ ケ\ \ }} \gt 0$」...④
または
「$\cos\boxed{\boxed{\ \ ク\ \ }} \lt 0$ かつ $\sin\boxed{\boxed{\ \ ケ\ \ }} \lt 0$」...⑤
が成り立つことと同値であることがわかる。
$0 \leqq x \leqq \pi$のとき、④,⑤により、$\sin 4x$>$\sin 3x$が成り立つようなxの値の範囲は
$0 \leqq x \leqq \displaystyle\frac{\pi}{\boxed{\ \ コ\ \ }}$, $\displaystyle\frac{\boxed{\ \ サ\ \ }}{\boxed{\ \ シ\ \ }}\pi \lt x \lt \frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}\pi$
である。
$\boxed{\boxed{\ \ ク\ \ }}$, $\boxed{\boxed{\ \ ケ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪0 ①x ②2x ③3x
④4x ⑤5x ⑥6x ⑦$\frac{x}{2}$
⑧$\frac{3}{2}x$ ⑨$\frac{5}{2}x$ ⓐ$\frac{7}{2}x$ ⓑ$\frac{9}{2}x$
(4)(2), (3)の考察から、$0 \leqq x \leqq \pi$のとき、$\sin 3x \gt \sin 4x \gt \sin 2x$が成り立つようなxの値の範囲は
$\displaystyle\frac{\pi}{\boxed{\ \ コ\ \ }}$ $\lt$ $\displaystyle\frac{\pi}{\boxed{\ \ ソ\ \ }}$, $\displaystyle\frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}\pi \lt x \lt \frac{\boxed{\ \ タ\ \ }}{\boxed{\ \ チ\ \ }}\pi$
であることがわかる。
[ 2 ]
(1)$a \gt 0$, $a \ne 1$, $b \gt 0$のとき、$\log_ab=x$とおくと、$\boxed{\boxed{\ \ ツ\ \ }}$が成り立つ。
$\boxed{\boxed{\ \ ツ\ \ }}$の解答群
⓪$x^a=b$ ①$x^b=a$ ②$a^x=b$
③$b^x=a$ ④$a^b=x$ ⑤$b^a=x$
(2)様々な対数の値が有理数か無理数かについて考えよう。
(i)$\log_5 25=\boxed{\ \ テ\ \ }$, $\log_9 27=\displaystyle\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}$であり、どちらも有理数である。
(ii)$\log_2 3$が有理数と無理数のどちらかであるかを考えよう。
$\log_2 3$が有理数であると仮定すると、$\log_2 3$>0であるので、二つの自然数p, qを用いて$\log_2 3=\displaystyle\frac{p}{q}$と表すことができる。このとき、(1)により$\log_2 3=\displaystyle\frac{p}{q}$は$\boxed{\boxed{\ \ ニ\ \ }}$と変形できる。いま、2は偶数であり3は奇数であるので、$\boxed{\boxed{\ \ ニ\ \ }}$を満たす自然数p, qは存在しない。
したがって、$\log_2 3$は無理数であることがわかる。
(iii)a, bを2以上の自然数とするとき、(ii)と同様に考えると、「$\boxed{\boxed{\ \ ヌ\ \ }}$ならば$\log_a b$は常に無理数である」ことがわかる。
$\boxed{\boxed{\ \ ヌ\ \ }}$の解答群
⓪aが偶数 ①bが偶数 ②aが奇数
③bが奇数 ④aとbがともに偶数、またはaとbがともに奇数 ⑤aとbのいずれか一方が偶数で、もう一方が奇数
2023共通テスト過去問
この動画を見る
第一問
[ 1 ] 三角関数の値の大小関係について考えよう。
(1) $x=\displaystyle\frac{\pi}{6}$のとき$\sin x\boxed{\boxed{\ \ ア\ \ }}\sin 2x$であり、$x=\frac{2}{3}\pi$のとき$\sin x\boxed{\boxed{\ \ イ\ \ }}\sin 2x$である。
$\boxed{\boxed{\ \ ア\ \ }}$, $\boxed{\boxed{\ \ イ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪< ①= ②>
(2) $\sin x$と$\sin 2x$の値の大小関係を詳しく調べよう。
$\sin 2x$-$\sin x$=$\sin 2x\left(\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ }\right)$
であるから、$\sin 2x$-$\sin x$>0が成り立つことは
「$\sin x$>0かつ $\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ } \gt 0$」... ①
「$\sin x$<0かつ $\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ } \lt 0$」... ②
が成り立つことと同値である。$0 \leqq x \leqq 2\pi$のとき、①が成り立つようなxの値の範囲は
$0 \lt x \lt \displaystyle\frac{\pi}{\boxed{\ \ オ\ \ }}$
であり、②が成り立つようなxの値の範囲は
$\pi \lt x \lt \displaystyle\frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ\ \ }}\pi$
である。よって、$0 \leqq x \leqq 2\pi$のとき、$\sin 2x \gt \sin x$が成り立つようなxの値の範囲は
$0 \lt x \lt \displaystyle\frac{\pi}{\boxed{\ \ オ\ \ }}, \pi \lt x \lt \displaystyle\frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ\ \ }}\pi$
である。
(3)$\sin 3x$と$\sin 4x$の値の大小関係を調べよう。
三角関数の加法定理を用いると、等式
$\sin(\alpha+\beta)$-$\sin(\alpha-\beta)$=$2\cos\alpha\sin\beta$...③
が得られる。$\alpha+\beta=4x$, $\alpha-\beta=3x$を満たす$\alpha$, $\beta$に対して③を用いることにより、$\sin 4x-\sin 3x \gt 0$が成り立つことは
「$\cos\boxed{\boxed{\ \ ク\ \ }} \gt 0$ かつ $\sin\boxed{\boxed{\ \ ケ\ \ }} \gt 0$」...④
または
「$\cos\boxed{\boxed{\ \ ク\ \ }} \lt 0$ かつ $\sin\boxed{\boxed{\ \ ケ\ \ }} \lt 0$」...⑤
が成り立つことと同値であることがわかる。
$0 \leqq x \leqq \pi$のとき、④,⑤により、$\sin 4x$>$\sin 3x$が成り立つようなxの値の範囲は
$0 \leqq x \leqq \displaystyle\frac{\pi}{\boxed{\ \ コ\ \ }}$, $\displaystyle\frac{\boxed{\ \ サ\ \ }}{\boxed{\ \ シ\ \ }}\pi \lt x \lt \frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}\pi$
である。
$\boxed{\boxed{\ \ ク\ \ }}$, $\boxed{\boxed{\ \ ケ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪0 ①x ②2x ③3x
④4x ⑤5x ⑥6x ⑦$\frac{x}{2}$
⑧$\frac{3}{2}x$ ⑨$\frac{5}{2}x$ ⓐ$\frac{7}{2}x$ ⓑ$\frac{9}{2}x$
(4)(2), (3)の考察から、$0 \leqq x \leqq \pi$のとき、$\sin 3x \gt \sin 4x \gt \sin 2x$が成り立つようなxの値の範囲は
$\displaystyle\frac{\pi}{\boxed{\ \ コ\ \ }}$ $\lt$ $\displaystyle\frac{\pi}{\boxed{\ \ ソ\ \ }}$, $\displaystyle\frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}\pi \lt x \lt \frac{\boxed{\ \ タ\ \ }}{\boxed{\ \ チ\ \ }}\pi$
であることがわかる。
[ 2 ]
(1)$a \gt 0$, $a \ne 1$, $b \gt 0$のとき、$\log_ab=x$とおくと、$\boxed{\boxed{\ \ ツ\ \ }}$が成り立つ。
$\boxed{\boxed{\ \ ツ\ \ }}$の解答群
⓪$x^a=b$ ①$x^b=a$ ②$a^x=b$
③$b^x=a$ ④$a^b=x$ ⑤$b^a=x$
(2)様々な対数の値が有理数か無理数かについて考えよう。
(i)$\log_5 25=\boxed{\ \ テ\ \ }$, $\log_9 27=\displaystyle\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}$であり、どちらも有理数である。
(ii)$\log_2 3$が有理数と無理数のどちらかであるかを考えよう。
$\log_2 3$が有理数であると仮定すると、$\log_2 3$>0であるので、二つの自然数p, qを用いて$\log_2 3=\displaystyle\frac{p}{q}$と表すことができる。このとき、(1)により$\log_2 3=\displaystyle\frac{p}{q}$は$\boxed{\boxed{\ \ ニ\ \ }}$と変形できる。いま、2は偶数であり3は奇数であるので、$\boxed{\boxed{\ \ ニ\ \ }}$を満たす自然数p, qは存在しない。
したがって、$\log_2 3$は無理数であることがわかる。
(iii)a, bを2以上の自然数とするとき、(ii)と同様に考えると、「$\boxed{\boxed{\ \ ヌ\ \ }}$ならば$\log_a b$は常に無理数である」ことがわかる。
$\boxed{\boxed{\ \ ヌ\ \ }}$の解答群
⓪aが偶数 ①bが偶数 ②aが奇数
③bが奇数 ④aとbがともに偶数、またはaとbがともに奇数 ⑤aとbのいずれか一方が偶数で、もう一方が奇数
2023共通テスト過去問
2023共通テスト 正弦定理で解く!?こんな解き方もあり?

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
円の半径=5
$sin\angle ACB = $
*図は動画内参照
2023共通テスト数ⅠA
この動画を見る
円の半径=5
$sin\angle ACB = $
*図は動画内参照
2023共通テスト数ⅠA
【満点続出】篠原塾の塾生の結果報告【共通テスト2023】

共通テストだけど中学生も解ける!!
単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
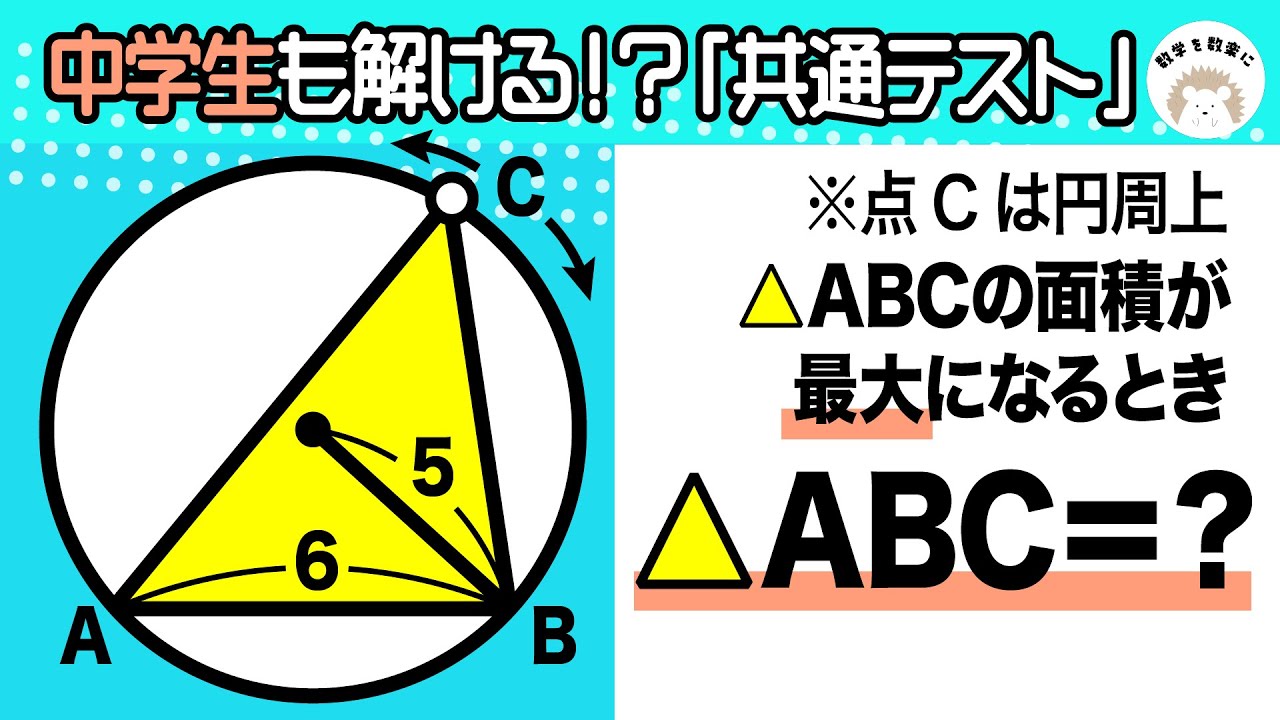
△ABCの面積が最大になるとき△ABC=?
*点Cは円周上
*図は動画内参照
2023共通テスト数ⅠA
この動画を見る
△ABCの面積が最大になるとき△ABC=?
*点Cは円周上
*図は動画内参照
2023共通テスト数ⅠA
2023年共通テスト数学2B講評【まさかの和積の公式登場】

単元:
#大学入試過去問(数学)#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
ユーテラ授業チャンネル【YouTubeの寺子屋】
問題文全文(内容文):
2023年共通テスト「和積の公式」の講評です。
※問題文は動画内参照
この動画を見る
2023年共通テスト「和積の公式」の講評です。
※問題文は動画内参照
2023年共通テスト数学1A講評【易化】

単元:
#大学入試過去問(数学)#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
Morite2 English Channel
問題文全文(内容文):
2023年共通テスト数学1Aを講評します。
各問題の解き方や、注意すべき点を確認しましょう。
復習の参考にしましょう!
この動画を見る
2023年共通テスト数学1Aを講評します。
各問題の解き方や、注意すべき点を確認しましょう。
復習の参考にしましょう!
【日本最速解答速報】共通テスト2023数学1A 第5問

【日本最速解答速報】共通テスト2023数学2B 第2問・第4問

