 小樽商科大学
小樽商科大学
 小樽商科大学
小樽商科大学
#小樽商科大学#不定積分#ますただ
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#小樽商科大学
指導講師:
ますただ
問題文全文(内容文):
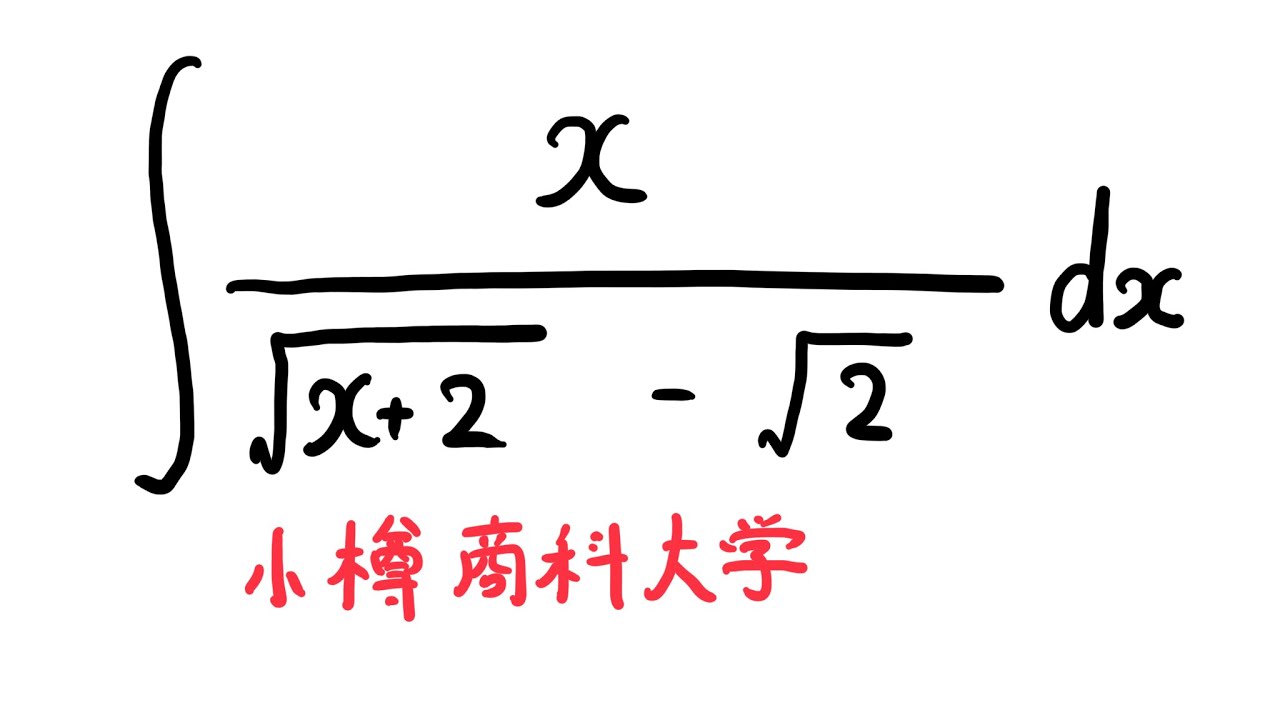
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ 2x+2}-\sqrt{ 2 }}$ $dx$
出典:小樽商科大学
この動画を見る
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ 2x+2}-\sqrt{ 2 }}$ $dx$
出典:小樽商科大学
大学入試問題#852「これは、大変・・・グラフでもいけるんかなー」 #小樽商科大学(2018) #整数問題

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#小樽商科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \frac{2n-2}{n^2+2n+2}$が整数となるような整数$n$をすべて求めよ
出典:2018年小樽商科大学
この動画を見る
$\displaystyle \frac{2n-2}{n^2+2n+2}$が整数となるような整数$n$をすべて求めよ
出典:2018年小樽商科大学
大学入試問題#429「誘導があってもよいような・・・」 小樽商科大学 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#小樽商科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} (1-x^2)^{\frac{5}{2}} dx$
出典:小樽商科大学
この動画を見る
$\displaystyle \int_{0}^{1} (1-x^2)^{\frac{5}{2}} dx$
出典:小樽商科大学
大学入試問題#85 小樽商科大学(1988) 不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#小樽商科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \sin(log\ x)dx$を計算せよ。
出典:1988年小樽商科大学 入試問題
この動画を見る
$\displaystyle \int \sin(log\ x)dx$を計算せよ。
出典:1988年小樽商科大学 入試問題
小樽商科大 3次方程式 整数解 有理数解 高校数学 Mathematics Japanese university entrance exam

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#小樽商科大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
小樽商科大学過去問題
$x^3-3x-1=0$の解をα
次の(1)~(3)を示せ。
(1)αは整数でない
(2)αは有理数でない
(3)αは$p+q\sqrt3$(p,q有理数)の形ではない。
この動画を見る
小樽商科大学過去問題
$x^3-3x-1=0$の解をα
次の(1)~(3)を示せ。
(1)αは整数でない
(2)αは有理数でない
(3)αは$p+q\sqrt3$(p,q有理数)の形ではない。
