 順天堂大学
順天堂大学
 順天堂大学
順天堂大学
【高校化学】少ない暗記量で得点源にする糖類の解説(7)デンプン関連の計算問題をマスターしよう!

単元:
#化学#大学入試過去問(化学)#理科(高校生)#順天堂大学#工学院大学
指導講師:
ぺんぎん高校化学問題集
問題文全文(内容文):
デンプン100gを完全に加水分解すると何gのグルコース得られるか。有効数字2桁で答えよ。(2024 工学院大学)
9.72gのアメロペクチンAのヒドロキシ基をすべてCH₃O⁻(メトキシ基)にした後に希硫酸で完全に加水分解すると,分子量の異なるB, C, Dが得られ,CはDよりも多くのヒドロキシ基を持っていた。それぞれの収量はBが12.25g,Cが0.499g,Dが0.566gであった。なお,図中の①に相当する炭素に結合しているメトキシ基以外は加水分解を受けない。Aはグルコース単位で平均何個ごとに枝分かれするか。(2024 順天堂大学)
この動画を見る
デンプン100gを完全に加水分解すると何gのグルコース得られるか。有効数字2桁で答えよ。(2024 工学院大学)
9.72gのアメロペクチンAのヒドロキシ基をすべてCH₃O⁻(メトキシ基)にした後に希硫酸で完全に加水分解すると,分子量の異なるB, C, Dが得られ,CはDよりも多くのヒドロキシ基を持っていた。それぞれの収量はBが12.25g,Cが0.499g,Dが0.566gであった。なお,図中の①に相当する炭素に結合しているメトキシ基以外は加水分解を受けない。Aはグルコース単位で平均何個ごとに枝分かれするか。(2024 順天堂大学)
大学入試問題#736「茶番積分」 順天堂大学医学部(2024) 定積分
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#順天堂大学
指導講師:
ますただ
問題文全文(内容文):
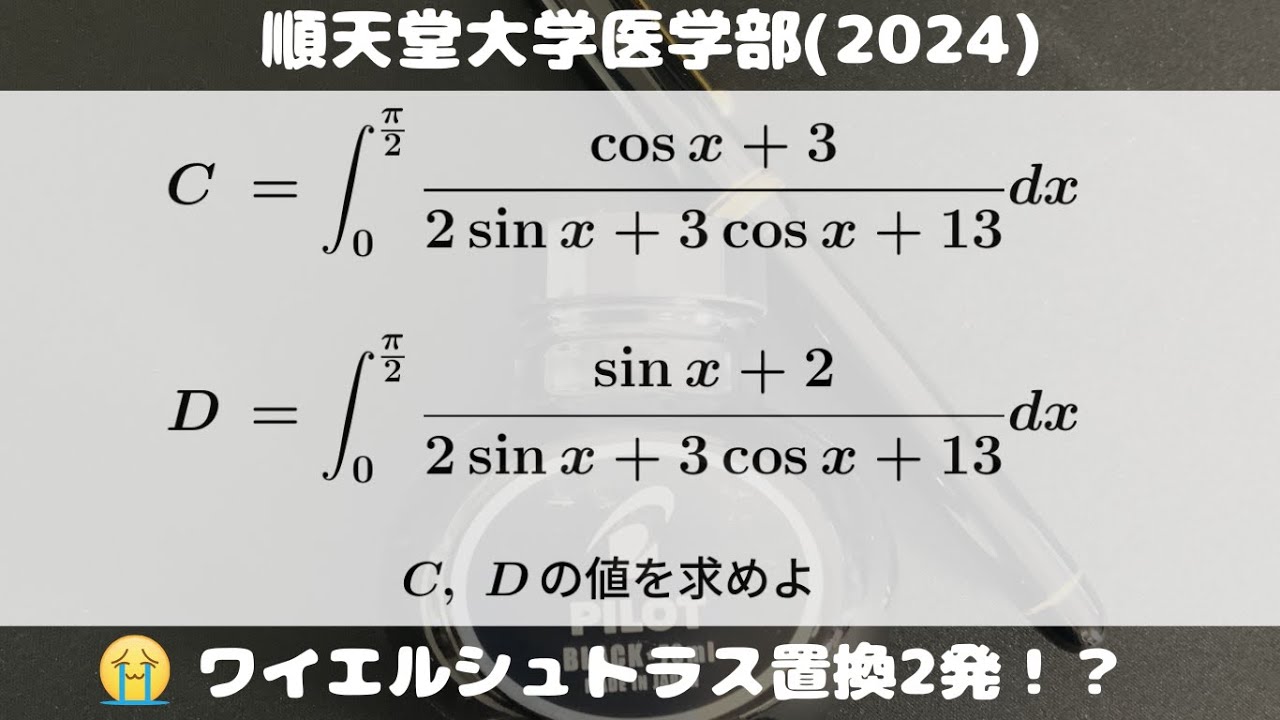
$C=\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{\cos\ x+3}{2\sin\ x+3\cos\ x+13} dx$
$D=\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{\sin\ x+2}{2\sin\ x+3\cos\ x+13} dx$
$C,D$の値を求めよ。
出典:2024年順天堂大学医学部 入試問題
この動画を見る
$C=\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{\cos\ x+3}{2\sin\ x+3\cos\ x+13} dx$
$D=\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{\sin\ x+2}{2\sin\ x+3\cos\ x+13} dx$
$C,D$の値を求めよ。
出典:2024年順天堂大学医学部 入試問題
3次方程式の解の公式 順天堂大(医)

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#複素数と方程式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)#順天堂大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$ x^3+9x+6=0$
*誘導あり
解には$ \omega^3=1$の$\omega$を用いる$(\omega\neq 1)$
順天堂大(医)過去問
この動画を見る
これを解け.
$ x^3+9x+6=0$
*誘導あり
解には$ \omega^3=1$の$\omega$を用いる$(\omega\neq 1)$
順天堂大(医)過去問
順天堂(医)確率 基本
単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#順天堂大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
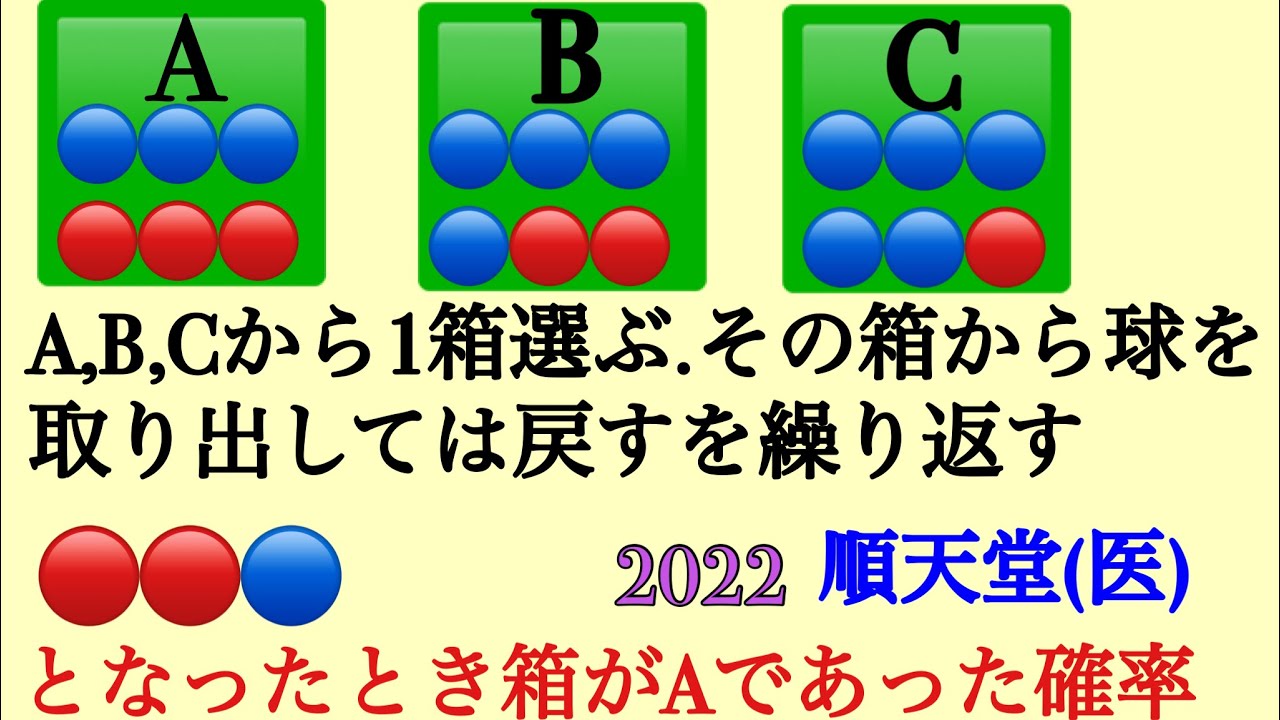
ある1つの箱から とり出して戻すを3回行ったら
●●○となった
箱がAである確率を求めよ
2022年順天堂医学大学 過去問
この動画を見る
ある1つの箱から とり出して戻すを3回行ったら
●●○となった
箱がAである確率を求めよ
2022年順天堂医学大学 過去問
順天堂大(医)等比数列の和の収束

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#数B#順天堂大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
{$a_n$}は等比数列
無限級数
$a_2+a_4+a_6+…$は$\displaystyle \frac{12}{5}$に収束
$a_3+a_6+a_9+…$は$\displaystyle \frac{24}{19}$に収束
{$a_n$}の公比、初項、無限階数$a_1+a_2+1_3+…$は[ ]に収束するか求めよ
出典:順天堂大学医学部 過去問
この動画を見る
{$a_n$}は等比数列
無限級数
$a_2+a_4+a_6+…$は$\displaystyle \frac{12}{5}$に収束
$a_3+a_6+a_9+…$は$\displaystyle \frac{24}{19}$に収束
{$a_n$}の公比、初項、無限階数$a_1+a_2+1_3+…$は[ ]に収束するか求めよ
出典:順天堂大学医学部 過去問
順天堂(医)複素数

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#学校別大学入試過去問解説(数学)#数学(高校生)#順天堂大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$z=\cos \displaystyle \frac{2}{7}\pi+i \sin \displaystyle \frac{2}{7}\pi$
$w=z+z^2+z^4$
(1)
①$w+\bar{ w }$
②$w・\bar{ w }$
(2)
①$\cos \displaystyle \frac{2}{7}\pi+\cos \displaystyle \frac{4}{7}\pi+\cos \displaystyle \frac{8}{7}\pi$
②$\sin \displaystyle \frac{2}{7}\pi+\sin \displaystyle \frac{4}{7}\pi+\sin \displaystyle \frac{8}{7}\pi$
出典:2019年順天堂大学医学部 過去問
この動画を見る
$z=\cos \displaystyle \frac{2}{7}\pi+i \sin \displaystyle \frac{2}{7}\pi$
$w=z+z^2+z^4$
(1)
①$w+\bar{ w }$
②$w・\bar{ w }$
(2)
①$\cos \displaystyle \frac{2}{7}\pi+\cos \displaystyle \frac{4}{7}\pi+\cos \displaystyle \frac{8}{7}\pi$
②$\sin \displaystyle \frac{2}{7}\pi+\sin \displaystyle \frac{4}{7}\pi+\sin \displaystyle \frac{8}{7}\pi$
出典:2019年順天堂大学医学部 過去問
順天堂・御茶ノ水女子 複素数 高校数学 Mathematics Japanese university entrance exam

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C#順天堂大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
順天堂大学過去問題
1⃣
$α^4+α^3+α^2+α+1=0$
$α^6(α^7+1)(α+1)$の値
2⃣
$\sqrt3 + i +z$の絶対値を最大にする複素数Z
ただし|Z|=1
この動画を見る
順天堂大学過去問題
1⃣
$α^4+α^3+α^2+α+1=0$
$α^6(α^7+1)(α+1)$の値
2⃣
$\sqrt3 + i +z$の絶対値を最大にする複素数Z
ただし|Z|=1
