その他
その他
みんなの入試では出るかな？
単元：
#その他#その他#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
2025という数字にまつわる、入試問題で応用されそうな知識を紹介する動画です
この動画を見る
2025という数字にまつわる、入試問題で応用されそうな知識を紹介する動画です
kの書き方何番？
誕生日に死ぬ確率が上がる理由は？
三人の中で自分の帽子の色が分かるのは？
これなんでか分かる？
みんなは何番？
単元：
#その他#その他#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
チャンネル登録はこれ✅
/ @akitonton
#勉強 #授業 #あきとんとん #教育系YouTuber #shorts
分かりやすかった，面白かったと思ったら高評価チャンネル登録お願いします．
質問等ございましたら，コメント，SNSでお寄せ下さい．
～～～～～～～～～～～～～～～～～～～～～～～
Instagram: / akitonton5
TikTok: / akitonton
twitter: / akitonton5
LINE：https://lin.ee/xg8a0Pu
https://timeline.line.me/user/_dabZdm...
自習室: https://akitonton.com
～～～～～～～～～～～～～～～～～～～～～～～
この動画を見る
チャンネル登録はこれ✅
/ @akitonton
#勉強 #授業 #あきとんとん #教育系YouTuber #shorts
分かりやすかった，面白かったと思ったら高評価チャンネル登録お願いします．
質問等ございましたら，コメント，SNSでお寄せ下さい．
～～～～～～～～～～～～～～～～～～～～～～～
Instagram: / akitonton5
TikTok: / akitonton
twitter: / akitonton5
LINE：https://lin.ee/xg8a0Pu
https://timeline.line.me/user/_dabZdm...
自習室: https://akitonton.com
～～～～～～～～～～～～～～～～～～～～～～～
π＝４って証明見たけど本当？
福田のおもしろ数学297〜1分チャレンジ！ 魔方陣
ずっとE判定...→絶対に〇〇をしてください【1.5倍速推奨】#カサニマロ
3分の1は無限だって？
【保存版】数学の無限∞の考え方
なんて書いた？黒板ASMRと思いきや...
2次方程式のすごい解法見つけた
連立方程式をあれで解こう
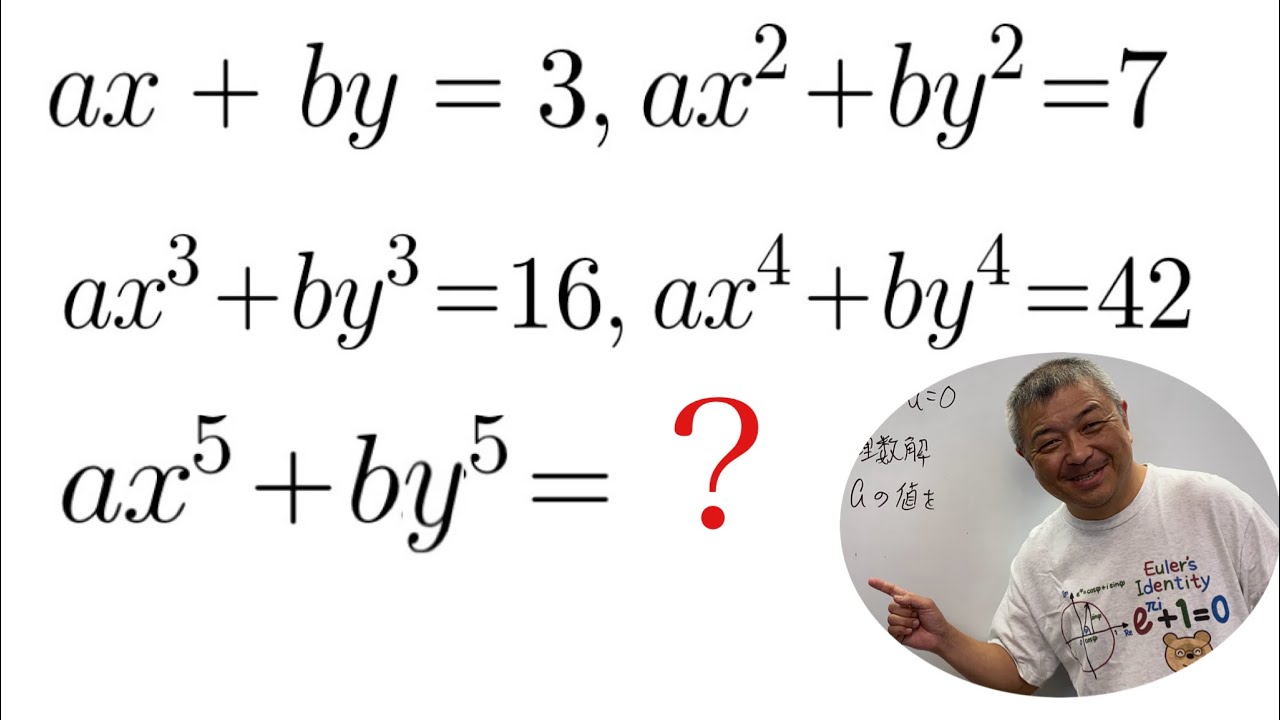
単元：
#その他#その他#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ax+ay=3$
$ax^2+ay^2=7$
$ax^3+by^3=16$
$ax^4+by^4=42$
のとき、
$ax^5+by^5$の値を求めよ
この動画を見る
$ax+ay=3$
$ax^2+ay^2=7$
$ax^3+by^3=16$
$ax^4+by^4=42$
のとき、
$ax^5+by^5$の値を求めよ
みんなはどうする？
【レベル別】コンパスなしで円を書く方法
やっぱり天才だったもえぴちゃん
単元：
#その他#その他#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
$\displaystyle \sum_{k=1}^\infty \frac{1}{k^2}$
を求めよ
この動画を見る
$\displaystyle \sum_{k=1}^\infty \frac{1}{k^2}$
を求めよ
【数学】入試で「大学レベル」の解法を使ったら減点されるのか？
単元：
#その他#勉強法#その他#数学(高校生)#その他
指導講師：
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文)：
【数学】入試で「大学レベル」の解法を使ったら減点されるか解説していきます。
この動画を見る
【数学】入試で「大学レベル」の解法を使ったら減点されるか解説していきます。
【数学】絶対に「時間配分」でミスらなくなる方法
単元：
#その他#勉強法#その他#数学(高校生)#その他
指導講師：
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文)：
【数学】絶対に「時間配分」でミスらなくなる方法を解説していきます。
この動画を見る
【数学】絶対に「時間配分」でミスらなくなる方法を解説していきます。
【数学】計算ミスを撲滅する５つのライフハック
【数学】いわゆる「難問・奇問」も勉強するべきか？
単元：
#その他#勉強法#その他#勉強法#数学(高校生)
指導講師：
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文)：
【数学】いわゆる「難問・奇問」の勉強を解説していきます。
この動画を見る
【数学】いわゆる「難問・奇問」の勉強を解説していきます。
【数学】復習に時間がかかりすぎるなら、試してほしい勉強法。
単元：
#その他#勉強法#その他#勉強法#数学(高校生)
指導講師：
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文)：
【数学】復習に時間がかかる場合に試してほしい勉強法を解説していきます。
この動画を見る
【数学】復習に時間がかかる場合に試してほしい勉強法を解説していきます。
x＋y🟰❓
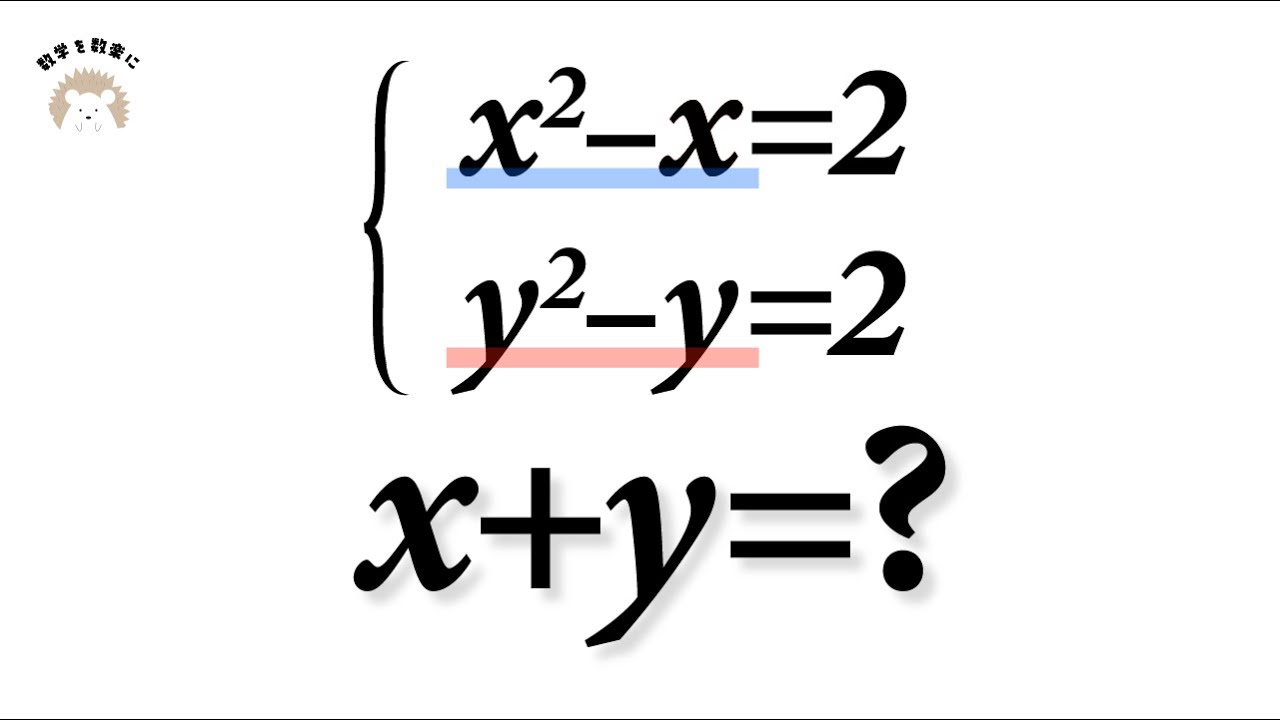
福田のおもしろ数学199〜偽造硬貨の山を見つけろ
単元：
#その他#その他#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$10$枚の効果を積み重ねた山が$10$本ある。どれも外見では区別ができないが、そのうちの$1$本の山はすべて偽造硬貨。残りの山は本物の硬貨だ。また、本物の硬貨は$10$グラムで偽造硬貨は$11$グラムであることがわかっている。$1$グラム単位で最大$2$キログラムまで量れる秤を使って偽造硬貨の山をいつけるには最低何回の計測が必要か？
この動画を見る
$10$枚の効果を積み重ねた山が$10$本ある。どれも外見では区別ができないが、そのうちの$1$本の山はすべて偽造硬貨。残りの山は本物の硬貨だ。また、本物の硬貨は$10$グラムで偽造硬貨は$11$グラムであることがわかっている。$1$グラム単位で最大$2$キログラムまで量れる秤を使って偽造硬貨の山をいつけるには最低何回の計測が必要か？
みんなは何問分かった？
これ知ってる？
福田のおもしろ数学195〜絶対分かる！オイラーの等式
夏の東大・京大模試でA判定を獲る勉強法（数学編）
単元：
#その他#勉強法#その他#勉強法#数学(高校生)
指導講師：
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文)：
夏の東大・京大模試でA判定を獲る勉強法（数学編)を解説していきます。
この動画を見る
夏の東大・京大模試でA判定を獲る勉強法（数学編)を解説していきます。
これできる？
単元：
#その他#その他#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
これできる？
【問題文】これのどこが間違っているか？
(-48)÷6÷(-2)
=(-48)÷(-3)
=16
この動画を見る
これできる？
【問題文】これのどこが間違っているか？
(-48)÷6÷(-2)
=(-48)÷(-3)
=16
【数学】京大に受かりたいなら覚えておくべき解法３選
単元：
#その他#勉強法#数学(高校生)
指導講師：
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文)：
「京大に受かりたいなら覚えておくべき数学対策３選」についてお話しています。
この動画を見る
「京大に受かりたいなら覚えておくべき数学対策３選」についてお話しています。