 2次関数とグラフ
2次関数とグラフ
 2次関数とグラフ
2次関数とグラフ
ガウス記号!これは取りたい!【早稲田大学】【数学 入試問題】

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次関数とグラフ#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
次の等式を満たす最大の整数aは、a=?である。
[$\displaystyle \frac{a}{2}$]+[$\displaystyle \frac{2a}{3}$]=a
但し、実数xに対して、$\lbrack x \rbrack$は、x以下の最大の整数を表す。
この動画を見る
次の等式を満たす最大の整数aは、a=?である。
[$\displaystyle \frac{a}{2}$]+[$\displaystyle \frac{2a}{3}$]=a
但し、実数xに対して、$\lbrack x \rbrack$は、x以下の最大の整数を表す。
2次関数 4STEP数Ⅰ 233,234,235 グラフと2次不等式4【ホーン・フィールドがていねいに解説】

単元:
#数Ⅰ#2次関数#2次方程式と2次不等式#2次関数とグラフ#数学(高校生)
教材:
#4STEP(4ステップ)数学#4STEP数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
1 (4STEP問題233)
次の関数のグラフをかけ。
(1)y=|2x+1|
(2)y=|x²+x|
(3)y=|x²-3x-4|
2 (4STEP問題234)
次の関数のグラフをかけ。
(1)y=x²-4|x|
(2)y=|x+1|(x-3)
3 (4STEP問題235)
次の関数のグラフをかけ。
(1)y=|x|+|x-1|
(2)y=|x+1|-|x-2|
この動画を見る
1 (4STEP問題233)
次の関数のグラフをかけ。
(1)y=|2x+1|
(2)y=|x²+x|
(3)y=|x²-3x-4|
2 (4STEP問題234)
次の関数のグラフをかけ。
(1)y=x²-4|x|
(2)y=|x+1|(x-3)
3 (4STEP問題235)
次の関数のグラフをかけ。
(1)y=|x|+|x-1|
(2)y=|x+1|-|x-2|
2次関数 4STEP数Ⅰ 162 2次関数の最大最小・文章題3【マコちゃんねるがていねいに解説】

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4STEP(4ステップ)数学#4STEP数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
$AB=6\sqrt{3}、CA=9、∠C=90°$の三角形ABCがある。
$点Pは頂点CからAまで辺CA上を毎秒3の速さで進む。$
$点QはPと同時に頂点Bを出発し、頂点Cまで辺BC上を毎秒\sqrt{3}の速さで進む。$
$このP,Q間の距離の最小値を求めよ。$
この動画を見る
$AB=6\sqrt{3}、CA=9、∠C=90°$の三角形ABCがある。
$点Pは頂点CからAまで辺CA上を毎秒3の速さで進む。$
$点QはPと同時に頂点Bを出発し、頂点Cまで辺BC上を毎秒\sqrt{3}の速さで進む。$
$このP,Q間の距離の最小値を求めよ。$
2次関数 4STEP数Ⅰ 161 2次関数の最大最小・文章題2【マコちゃんねるがていねいに解説】

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4STEP(4ステップ)数学#4STEP数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
点P(t,t²)は放物線y=x²上の点で、2点A(-1,1)、B(4,16)の間にある。このとき、三角形APBの面積の最大値を求めよ。
この動画を見る
点P(t,t²)は放物線y=x²上の点で、2点A(-1,1)、B(4,16)の間にある。このとき、三角形APBの面積の最大値を求めよ。
2次関数 4STEP数Ⅰ 160 2次関数の最大最小・文章題1【マコちゃんねるがていねいに解説】

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4STEP(4ステップ)数学#4STEP数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
周囲の長さが24cmである長方形について、次の問いに答えよ。
(1) この長方形の面積の最大値を求めよ。また、そのとき、長方形はどのような形か。
(2) この長方形の対角線を1辺とする正方形の面積の最小値を求めよ。
この動画を見る
周囲の長さが24cmである長方形について、次の問いに答えよ。
(1) この長方形の面積の最大値を求めよ。また、そのとき、長方形はどのような形か。
(2) この長方形の対角線を1辺とする正方形の面積の最小値を求めよ。
2次関数 4STEP数Ⅰ 159 2次関数の最大最小・場合分け3【マコちゃんねるがていねいに解説】

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4STEP(4ステップ)数学#4STEP数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
関数f(x)=-x²+2x+2 (a≦x≦a+1)の最大値をM(a)、最小値をm(a)とする。
(1) M(a)を求め、b=M(a)のグラフをかけ
(2) m(a)を求め、b=m(a)のグラフをかけ
この動画を見る
関数f(x)=-x²+2x+2 (a≦x≦a+1)の最大値をM(a)、最小値をm(a)とする。
(1) M(a)を求め、b=M(a)のグラフをかけ
(2) m(a)を求め、b=m(a)のグラフをかけ
2次関数 4STEP数Ⅰ 158 2次関数の最大最小・場合分け2【マコちゃんねるがていねいに解説】

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4STEP(4ステップ)数学#4STEP数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
aは定数とする。関数y=x²-2x+1 (a≦x≦a+1)について
(1) 最小値を求めよ
(2) 最大値を求めよ
この動画を見る
aは定数とする。関数y=x²-2x+1 (a≦x≦a+1)について
(1) 最小値を求めよ
(2) 最大値を求めよ
2次関数 4STEP数Ⅰ 157 2次関数の最大最小・場合分け1【マコちゃんねるがていねいに解説】

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4STEP(4ステップ)数学#4STEP数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
関数y=x²-2x+mの値が0≦x≦3の範囲で常に負となるように、定数mの値の範囲を定めよ
この動画を見る
関数y=x²-2x+mの値が0≦x≦3の範囲で常に負となるように、定数mの値の範囲を定めよ
2次関数 4STEP数Ⅰ 127,128 1次関数グラフの範囲【いつものシミズ君がていねいに解説】

単元:
#数学(中学生)#中2数学#数Ⅰ#2次関数#1次関数#2次関数とグラフ#数学(高校生)
教材:
#4STEP(4ステップ)数学#4STEP数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
【1】次の条件を満たすように、定数a,bの値を求めよ
(1)y=ax+bが x=-2のとき y=5 x=1のとき y=2
(2)y=ax+bが(-1、-1)(3,1)を通る
【2】次の条件を満たすように、定数a,bの値を求めよ
(1)y=3x+b(0≦x≦4)の地域が1≦y≦19である
(2)y=ax+b(1≦x≦3)の地域が0≦y≦1である
ただしa<0
この動画を見る
【1】次の条件を満たすように、定数a,bの値を求めよ
(1)y=ax+bが x=-2のとき y=5 x=1のとき y=2
(2)y=ax+bが(-1、-1)(3,1)を通る
【2】次の条件を満たすように、定数a,bの値を求めよ
(1)y=3x+b(0≦x≦4)の地域が1≦y≦19である
(2)y=ax+b(1≦x≦3)の地域が0≦y≦1である
ただしa<0
2次関数 4STEP数Ⅰ 156 2次関数最大最小場合分け5 【マコちゃんねるがていねいに解説】

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4STEP(4ステップ)数学#4STEP数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
kは定数とする。2次関数 y=x²+2kx+k の最小値をmとする。
(1) mはkの関数である。mをkの式で表せ。
(2) kの関数mの最大値とそのときのkの値を求めよ。
この動画を見る
kは定数とする。2次関数 y=x²+2kx+k の最小値をmとする。
(1) mはkの関数である。mをkの式で表せ。
(2) kの関数mの最大値とそのときのkの値を求めよ。
2次関数 4STEP数Ⅰ 155 2次関数最大最小場合分け4【マコちゃんねるがていねいに解説】

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4STEP(4ステップ)数学#4STEP数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
a>0とする。関数y=ax²+2ax+b (-2≦x≦1)の最大値が6、最小値が3であるように、定数a,bの値を定めよ。
この動画を見る
a>0とする。関数y=ax²+2ax+b (-2≦x≦1)の最大値が6、最小値が3であるように、定数a,bの値を定めよ。
2次関数 4STEP数Ⅰ 154 2次関数最大最小場合分け3【マコちゃんねるがていねいに解説】

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4STEP(4ステップ)数学#4STEP数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
関数y=x²-2ax-a (0≦x≦2)の最小値が-2であるように、定数aの値を定めよ。
この動画を見る
関数y=x²-2ax-a (0≦x≦2)の最小値が-2であるように、定数aの値を定めよ。
2次関数 4STEP数Ⅰ 153 2次関数最大最小場合分け2【マコちゃんねるがていねいに解説】

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4STEP(4ステップ)数学#4STEP数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
a<0とする。関数y=-x²+2ax+3a (0≦x≦1)の最小値が-11であるように、定数aの値を定めよ。
この動画を見る
a<0とする。関数y=-x²+2ax+3a (0≦x≦1)の最小値が-11であるように、定数aの値を定めよ。
2次関数 4STEP数Ⅰ 152 2次関数最大最小場合分け1 【マコちゃんねるがていねいに解説】

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4STEP(4ステップ)数学#4STEP数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
aを定数とする。
2次関数 y=-x²+2ax (0≦x≦1)の最大値をM(a)とするとき、次の問いに答えよ。
(1) M(a)を求めよ
(2) b=M(a)のグラフをかけ。
この動画を見る
aを定数とする。
2次関数 y=-x²+2ax (0≦x≦1)の最大値をM(a)とするとき、次の問いに答えよ。
(1) M(a)を求めよ
(2) b=M(a)のグラフをかけ。
ただの連立方程式だよね
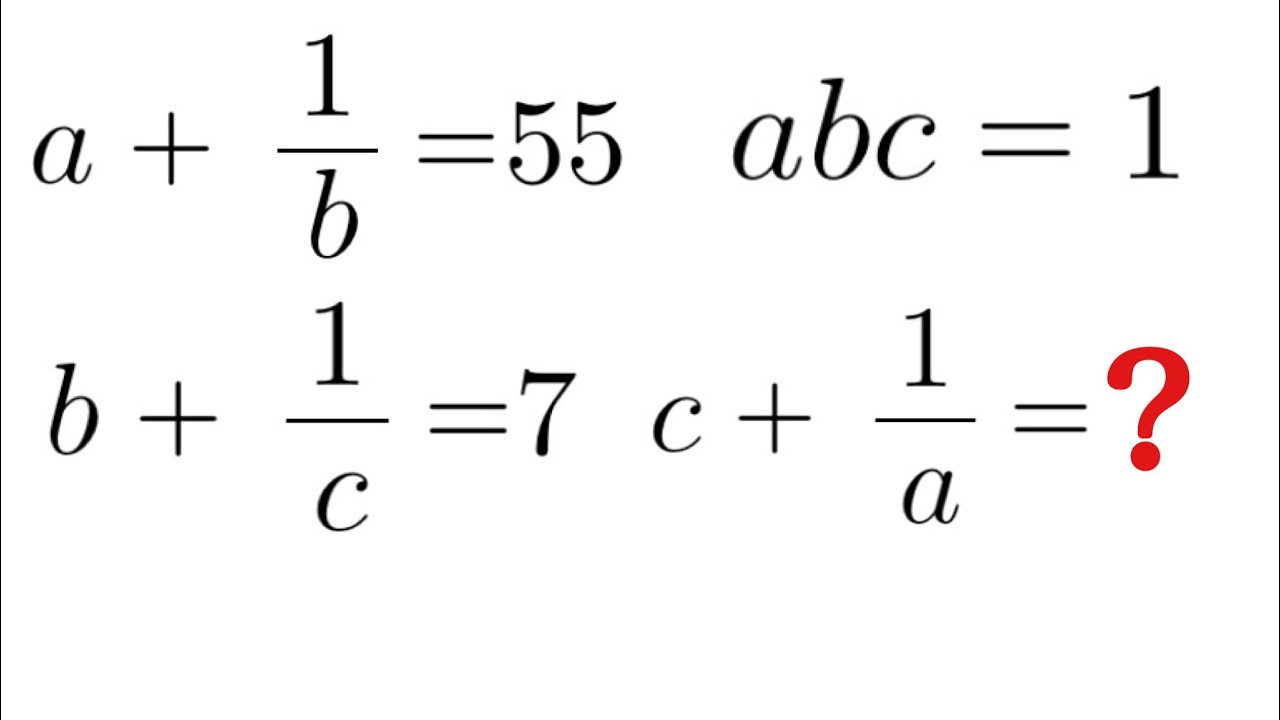
単元:
#数学(中学生)#中2数学#連立方程式#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$abc=1$
$a+\frac{1}{b}=55$
$b+\frac{1}{c}=7$
$C+\frac{1}{a}=?$
この動画を見る
$abc=1$
$a+\frac{1}{b}=55$
$b+\frac{1}{c}=7$
$C+\frac{1}{a}=?$
【マコちゃんねるがていねいに解説】2次関数 4STEP数Ⅰ 151 2次関数最大最小(3)

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4STEP(4ステップ)数学#4STEP数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
aは定数とする。関数y=-x²+4ax-2 (0≦x≦2)について、次の問いに答えよ。
(1) 最大値を求めよ。
(2) 最小値を求めよ。
この動画を見る
aは定数とする。関数y=-x²+4ax-2 (0≦x≦2)について、次の問いに答えよ。
(1) 最大値を求めよ。
(2) 最小値を求めよ。
【マコちゃんねるがていねいに解説】2次関数 4STEP数Ⅰ 150 2次関数最大最小(2)

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4STEP(4ステップ)数学#4STEP数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
aは定数とする。関数y=3x²-6ax+2 (0≦x≦2)について、次の問いに答えよ。
(1) 最小値を求めよ。
(2) 最大値を求めよ。
この動画を見る
aは定数とする。関数y=3x²-6ax+2 (0≦x≦2)について、次の問いに答えよ。
(1) 最小値を求めよ。
(2) 最大値を求めよ。
【マコちゃんねるがていねいに解説】2次関数 4STEP数Ⅰ 149 2次関数最大最小(1)

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4STEP(4ステップ)数学#4STEP数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
aは正の定数とする。関数y=x²-2x-1 (0≦x≦a)について、次の問いに答えよ。
(1) 最小値を求めよ
(2) 最大値を求めよ
この動画を見る
aは正の定数とする。関数y=x²-2x-1 (0≦x≦a)について、次の問いに答えよ。
(1) 最小値を求めよ
(2) 最大値を求めよ
【マコちゃんねるがていねいに解説】2次関数 4STEP数Ⅰ 144 場合分け関数のグラフ

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4STEP(4ステップ)数学#4STEP数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数のグラフをかけ。
(1) y=-x+2 (x<2) , y=x-2 (x≧2)
(2) y=1 (x<0) , y=x+1 (x≧0)
(3) y=x² (x<0) , y=x (0≦x<1) , y=-x²+2x (1≦x)
この動画を見る
次の関数のグラフをかけ。
(1) y=-x+2 (x<2) , y=x-2 (x≧2)
(2) y=1 (x<0) , y=x+1 (x≧0)
(3) y=x² (x<0) , y=x (0≦x<1) , y=-x²+2x (1≦x)
【数検準2級】高校数学:数学検定準2級2次:問4

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
問4. a,bを定数とします。放物線 y = -x² + 4ax + b について、次の問いに答えなさい。
(5) 頂点の座標をa,bを用いて表しなさい。この問題は答えだけを書いてください。
(6) 放物線 y = -x² をx軸方向に1、y軸方向に5だけ平行移動したところ、上の放物線になりました。このとき、a,bの値を
それぞれ求めなさい。
この動画を見る
問4. a,bを定数とします。放物線 y = -x² + 4ax + b について、次の問いに答えなさい。
(5) 頂点の座標をa,bを用いて表しなさい。この問題は答えだけを書いてください。
(6) 放物線 y = -x² をx軸方向に1、y軸方向に5だけ平行移動したところ、上の放物線になりました。このとき、a,bの値を
それぞれ求めなさい。
【野本さんちのツトムくんがていねいに解説】2次関数 4STEP数Ⅰ 172,173,174 2次関数の決定

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4STEP(4ステップ)数学#4STEP数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
172 次の条件を満たすような放物線の方程式を求めよ。
(1) 放物線 y=-3x²+x-1を平行移動した曲線で,頂点が点(-2,3)である。
(2) 放物線 y=x²-3xを平行移動した曲線で,2点 (2,1),(4,5)を通る。
173 2つの放物線y=x²-3x, y=1/2x²+ax+bの頂点が一致するように,定数a,bの値を定めよ。
174(1) 放物線y=x²-3x十4を平行移動した曲線で,点(2, 4)を通り,頂点が直線y=2x+1上にある放物線の方程式を求めよ。
(2) 放物線y=-2x²+5xを平行移動した曲線で,点(1, -3)を通り,頂点が放物線y=x²十4上にある放物線の方程式を求めよ。
この動画を見る
172 次の条件を満たすような放物線の方程式を求めよ。
(1) 放物線 y=-3x²+x-1を平行移動した曲線で,頂点が点(-2,3)である。
(2) 放物線 y=x²-3xを平行移動した曲線で,2点 (2,1),(4,5)を通る。
173 2つの放物線y=x²-3x, y=1/2x²+ax+bの頂点が一致するように,定数a,bの値を定めよ。
174(1) 放物線y=x²-3x十4を平行移動した曲線で,点(2, 4)を通り,頂点が直線y=2x+1上にある放物線の方程式を求めよ。
(2) 放物線y=-2x²+5xを平行移動した曲線で,点(1, -3)を通り,頂点が放物線y=x²十4上にある放物線の方程式を求めよ。
【野本さんちのツトムくんがていねいに解説】2次関数 4STEP数Ⅰ 163,164 2次関数の最大と最小条件式つき

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4STEP(4ステップ)数学#4STEP数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
163
(1) 2x+y=1のとき,x²+y²の最小値を求めよ。
(2) x+2y+3=0のとき,xyの最大値を求めよ。
164
x≧O, y≧O, x+y=4のとき,xのとりうる値の範囲を求めよ。また、x²+2y²の最大値と最小値を求めよ。
この動画を見る
163
(1) 2x+y=1のとき,x²+y²の最小値を求めよ。
(2) x+2y+3=0のとき,xyの最大値を求めよ。
164
x≧O, y≧O, x+y=4のとき,xのとりうる値の範囲を求めよ。また、x²+2y²の最大値と最小値を求めよ。
【マコちゃんねるがていねいに解説】2次関数 4STEP数Ⅰ 143 二次関数の対称移動(3)

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4STEP(4ステップ)数学#4STEP数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
放物線y=2x²-4x+1を、直線y=-2に関して対称移動して得られる放物線の方程式を求めよ。
この動画を見る
放物線y=2x²-4x+1を、直線y=-2に関して対称移動して得られる放物線の方程式を求めよ。
【マコちゃんねるがていねいに解説】2次関数 4STEP数Ⅰ 142 二次関数の対称移動(2)

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4STEP(4ステップ)数学#4STEP数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある放物線を、x軸方向にー1、y軸方向にー3だけ平行移動し、さらにx軸に関して対称移動をしたら、放物線y=x²-2x+2に移った。もとの放物線の方程式を求めよ。
この動画を見る
ある放物線を、x軸方向にー1、y軸方向にー3だけ平行移動し、さらにx軸に関して対称移動をしたら、放物線y=x²-2x+2に移った。もとの放物線の方程式を求めよ。
【マコちゃんねるがていねいに解説】2次関数 4STEP数Ⅰ 141 二次関数の対称移動(1)

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4STEP(4ステップ)数学#4STEP数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の直線、放物線を、x軸、y軸、原点に関して、それぞれ対称移動して得られる直線、放物線の方程式を求めよ。
(1)y=-x+1
(2)y=2x²+x
(3)y=-x²-x-6
この動画を見る
次の直線、放物線を、x軸、y軸、原点に関して、それぞれ対称移動して得られる直線、放物線の方程式を求めよ。
(1)y=-x+1
(2)y=2x²+x
(3)y=-x²-x-6
【マコちゃんねるがていねいに解説】2次関数 4STEP数Ⅰ 140 二次関数の平行移動(4)

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4STEP(4ステップ)数学#4STEP数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
放物線y=x²-4x+3を、次の方向に平行移動して原点を通るようにした放物線の方程式を求めよ。
(1)y軸方向
(2)x軸方向
この動画を見る
放物線y=x²-4x+3を、次の方向に平行移動して原点を通るようにした放物線の方程式を求めよ。
(1)y軸方向
(2)x軸方向
【マコちゃんねるがていねいに解説】2次関数 4STEP数Ⅰ 139 二次関数の平行移動(3)

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4STEP(4ステップ)数学#4STEP数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の放物線をx軸方向に1、y軸方向に-2だけ平行移動して得られる放物線の方程式を求めよ。
(1)y=-x²
(2)y=2x²+4x
(3)y=3x²+x-4
この動画を見る
次の放物線をx軸方向に1、y軸方向に-2だけ平行移動して得られる放物線の方程式を求めよ。
(1)y=-x²
(2)y=2x²+4x
(3)y=3x²+x-4
【マコちゃんねるがていねいに解説】2次関数 4STEP数Ⅰ 138 二次関数の平行移動(2)

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4STEP(4ステップ)数学#4STEP数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
放物線y=x²-4x+4は、どのように平行移動すると放物線y=x²+2x-1に重なるか。
この動画を見る
放物線y=x²-4x+4は、どのように平行移動すると放物線y=x²+2x-1に重なるか。
【マコちゃんねるがていねいに解説】2次関数 4STEP数Ⅰ 137 二次関数の平行移動(1)

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4STEP(4ステップ)数学#4STEP数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
放物線y=-3x²を、頂点が次の点になるように平行移動するとき、移動後の放物線の方程式を求めよ。
(1) (1,2)
(2) (-2,3)
この動画を見る
放物線y=-3x²を、頂点が次の点になるように平行移動するとき、移動後の放物線の方程式を求めよ。
(1) (1,2)
(2) (-2,3)
【数Ⅰ】2次関数:【難問】場合分け嫌いな人必見!絶対値付き2次関数:本論

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
aを定数とする。xについての方程式 $│(x-2)(x-4)│=ax-5a+\dfrac{1}{2}$ が相異なる4つの実数解を持つときのaの値の範囲を求めよ。
場合分けの必要なし!
aの値によらず必ず通る定点を考慮する必要もなし!
できるだけラクをして正解にたどり着きましょう。
この動画を見る
aを定数とする。xについての方程式 $│(x-2)(x-4)│=ax-5a+\dfrac{1}{2}$ が相異なる4つの実数解を持つときのaの値の範囲を求めよ。
場合分けの必要なし!
aの値によらず必ず通る定点を考慮する必要もなし!
できるだけラクをして正解にたどり着きましょう。
