 数A
数A
 数A
数A
大学入試問題#10 慶応義塾大学(2021) 解と係数の関係の応用

単元:
#数A#整数の性質#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$0 \lt m:$整数
$x^3-20x^2+mx-2(m-1)=0$は3つの異なる正の整数解をもつとき、
$m$と3つの解を求めよ。
出典:2021年慶應義塾大学 入試問題
この動画を見る
$0 \lt m:$整数
$x^3-20x^2+mx-2(m-1)=0$は3つの異なる正の整数解をもつとき、
$m$と3つの解を求めよ。
出典:2021年慶應義塾大学 入試問題
慶應女子高校 整数問題 慶應大学理工学部の過去問!

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
平方の和で表せる2つの数の積は平方の和で表せることを証明せよ.
1962慶応理工過去問
この動画を見る
平方の和で表せる2つの数の積は平方の和で表せることを証明せよ.
1962慶応理工過去問
11愛知県教員採用試験(数学:3番 整数問題)

単元:
#数A#整数の性質#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$l,k:$自然数
$p:$素数
$l^2-k^2=21$
$p=l+k$を満たす$p,l,k$を求めよ。
この動画を見る
$l,k:$自然数
$p:$素数
$l^2-k^2=21$
$p=l+k$を満たす$p,l,k$を求めよ。
普通の中学生は、解けない。別解は概要欄、コメントに
【5分で知る!証明問題のストーリー!】整数:明治大学付属中野高等学校~全国入試問題解法

単元:
#数学(中学生)#整数の性質#高校入試過去問(数学)#明治大学付属明治高等学校#明治大学付属中野高等学校#明治大学付属中野高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 明治大学付属中野高等学校
3けたの正の整数において、上2けたの数から一の位の数を
引いた数が11の倍数
もとの3けたの 整数は、11の倍数 である。
この性質が成り立つわけを説明しなさい。
※3けたの正の整数の百の位の数をx、十の位の数をy、一の位の数をzとする
この動画を見る
入試問題 明治大学付属中野高等学校
3けたの正の整数において、上2けたの数から一の位の数を
引いた数が11の倍数
もとの3けたの 整数は、11の倍数 である。
この性質が成り立つわけを説明しなさい。
※3けたの正の整数の百の位の数をx、十の位の数をy、一の位の数をzとする
一橋大(類)整数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n^n+1$が7の倍数となる自然数$n$をすべて求めよ.
ただし,$n\leqq 50$である.
一橋大(類)過去問
この動画を見る
$n^n+1$が7の倍数となる自然数$n$をすべて求めよ.
ただし,$n\leqq 50$である.
一橋大(類)過去問
【5分でOK!思考力、対応力を高めるために!】整数:日本大学習志野高等学校~全国入試問題解法

単元:
#数学(中学生)#整数の性質#高校入試過去問(数学)#日本大学習志野高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 日本大学習志野高等学校
自然数Nの一の位を$《N》$で表すとき
$《2^{2021}》+《2^{117}》+《2^{56}》=$▭
この動画を見る
入試問題 日本大学習志野高等学校
自然数Nの一の位を$《N》$で表すとき
$《2^{2021}》+《2^{117}》+《2^{56}》=$▭
地道にやれば出るよね。パッと出す方法もいろいろありそう

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^4+x^3+x^2+x+1=0$のとき,
$\dfrac{x}{1+x^2}+\dfrac{x^2}{1+x^4}+\dfrac{x^3}{1+x}+\dfrac{x^4}{1+x^3}$の値を求めよ.
この動画を見る
$x^4+x^3+x^2+x+1=0$のとき,
$\dfrac{x}{1+x^2}+\dfrac{x^2}{1+x^4}+\dfrac{x^3}{1+x}+\dfrac{x^4}{1+x^3}$の値を求めよ.
この問題、間違えます
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
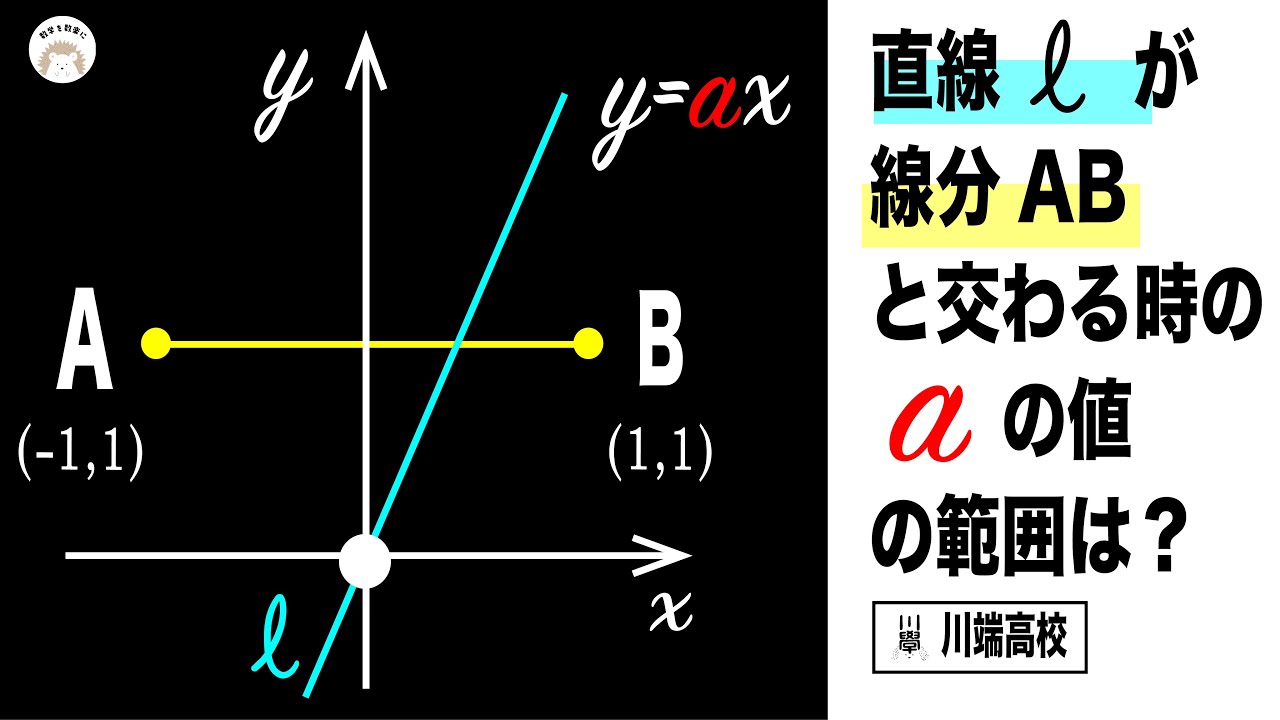
y=axが線分ABと交わるとき傾きaの値の範囲は?
*図は動画内参照
川端高校
この動画を見る
y=axが線分ABと交わるとき傾きaの値の範囲は?
*図は動画内参照
川端高校
福田の数学〜青山学院大学2021年理工学部第1問〜さいころの目の最大最小の確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#確率#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$1個のさいころを4回投げるとき、出た目の最小値をm、最大値をMとする。
(1)$m \geqq 2$となる確率は$\frac{\boxed{\ \ アイウ\ \ }}{\boxed{\ \ エオカキ\ \ }}$であり、
$m=1$となる確率は$\frac{\boxed{\ \ クケコ\ \ }}{\boxed{\ \ サシスセ\ \ }}$である。
(2)$m \geqq 2$かつ$M \leqq 5$となる確率は$\frac{\boxed{\ \ ソタ\ \ }}{\boxed{\ \ チツ\ \ }}$であり、$m \geqq 2$かつ$M=6$となる確率は
$\frac{\boxed{\ \ テト\ \ }}{\boxed{\ \ ナニヌ\ \ }}$である。
(3)$m=1$かつ$M=6$となる確率は$\frac{\boxed{\ \ ネノハ\ \ }}{\boxed{\ \ ヒフヘ\ \ }}$である。
2021青山学院大学理工学部過去問
この動画を見る
${\Large\boxed{1}}$1個のさいころを4回投げるとき、出た目の最小値をm、最大値をMとする。
(1)$m \geqq 2$となる確率は$\frac{\boxed{\ \ アイウ\ \ }}{\boxed{\ \ エオカキ\ \ }}$であり、
$m=1$となる確率は$\frac{\boxed{\ \ クケコ\ \ }}{\boxed{\ \ サシスセ\ \ }}$である。
(2)$m \geqq 2$かつ$M \leqq 5$となる確率は$\frac{\boxed{\ \ ソタ\ \ }}{\boxed{\ \ チツ\ \ }}$であり、$m \geqq 2$かつ$M=6$となる確率は
$\frac{\boxed{\ \ テト\ \ }}{\boxed{\ \ ナニヌ\ \ }}$である。
(3)$m=1$かつ$M=6$となる確率は$\frac{\boxed{\ \ ネノハ\ \ }}{\boxed{\ \ ヒフヘ\ \ }}$である。
2021青山学院大学理工学部過去問
対等性とは?僕と君は対等な関係 法政大学高校

単元:
#数学(中学生)#数A#場合の数と確率#確率#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
H,O,S,E,Iの5文字を1列に並べるときHがSより左にある場合の数を求めよ。
法政大学高等学校
この動画を見る
H,O,S,E,Iの5文字を1列に並べるときHがSより左にある場合の数を求めよ。
法政大学高等学校
【重心・内心・外心】三角形の○心はこう覚える!〔高校数学 数学〕

単元:
#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
三角形の重心・内心・外心について解説します。
この動画を見る
三角形の重心・内心・外心について解説します。
福田の数学〜上智大学2021年TEAP利用理系第3問〜複雑な試行の確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$南北方向にm区画、東西方向にn区画に区切られた長方形の土地がある。
この土地のそれぞれの区画にm種類の作物を1種類ずつ植える。ただし、南北方向に
は同じ種類の作物が植えられている区画はないようにする。このとき、東西方向に
隣り合う区画に同じ種類の作物が植えられている場合には、それらの区画は連結
した1個の畑とみなすとする。例えば、南北方向に3区画、東西方向に5区画で、
A,B,C3種類の作物を次のように植えた場合、畑が11個とみなす。
(1)$m=3$の時を考える。$n=1$ならば、畑の数は常に3個で、1通りある。
$n=2$ならば、畑の数は3個、5個、6個で3通りある。$n=3$ならば、畑の数は
$\boxed{\ \ ク\ \ }$通りある。$n=10$ならば、畑の数は$\boxed{\ \ ケ\ \ }$通りある。
(2)$m=3$で$n=3$のとき、畑の数が8個になる植え方は$\boxed{\ \ コ\ \ }$通りある。
(3)$m=6$のときを考える。各列の南北方向の6区画に作物を植える植え方は6!通り
あるが、それらすべてが等確率になるように植えることにする。$n=2$のとき、
畑が8個である確率は$\frac{\boxed{\ \ サ\ \ }}{\boxed{\ \ シ\ \ }}$であり、畑が9個である確率は$\frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}$であり、
畑が10個である確率は$\frac{\boxed{\ \ ソ\ \ }}{\boxed{\ \ タ\ \ }}$である。$n=3$のとき、
畑が10個である確率をpとすると$\boxed{\ \ け\ \ }$である。
$\boxed{\ \ け\ \ }$の選択肢:
$(\textrm{a})p \geqq \frac{1}{100} (\textrm{b})\frac{1}{200} \leqq p \lt \frac{1}{100} (\textrm{c})\frac{1}{500} \leqq p \lt \frac{1}{200}$
$(\textrm{d})\frac{1}{1000} \leqq p \lt \frac{1}{500} (\textrm{e})\frac{1}{2000} \leqq p \lt \frac{1}{1000} (\textrm{f})\frac{1}{5000} \leqq p \lt \frac{1}{2000}$
$(\textrm{g})\frac{1}{10000} \leqq p \lt \frac{1}{5000} (\textrm{h})p \lt \frac{1}{10000}$
2021上智大学理系過去問
この動画を見る
${\Large\boxed{3}}$南北方向にm区画、東西方向にn区画に区切られた長方形の土地がある。
この土地のそれぞれの区画にm種類の作物を1種類ずつ植える。ただし、南北方向に
は同じ種類の作物が植えられている区画はないようにする。このとき、東西方向に
隣り合う区画に同じ種類の作物が植えられている場合には、それらの区画は連結
した1個の畑とみなすとする。例えば、南北方向に3区画、東西方向に5区画で、
A,B,C3種類の作物を次のように植えた場合、畑が11個とみなす。
(1)$m=3$の時を考える。$n=1$ならば、畑の数は常に3個で、1通りある。
$n=2$ならば、畑の数は3個、5個、6個で3通りある。$n=3$ならば、畑の数は
$\boxed{\ \ ク\ \ }$通りある。$n=10$ならば、畑の数は$\boxed{\ \ ケ\ \ }$通りある。
(2)$m=3$で$n=3$のとき、畑の数が8個になる植え方は$\boxed{\ \ コ\ \ }$通りある。
(3)$m=6$のときを考える。各列の南北方向の6区画に作物を植える植え方は6!通り
あるが、それらすべてが等確率になるように植えることにする。$n=2$のとき、
畑が8個である確率は$\frac{\boxed{\ \ サ\ \ }}{\boxed{\ \ シ\ \ }}$であり、畑が9個である確率は$\frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}$であり、
畑が10個である確率は$\frac{\boxed{\ \ ソ\ \ }}{\boxed{\ \ タ\ \ }}$である。$n=3$のとき、
畑が10個である確率をpとすると$\boxed{\ \ け\ \ }$である。
$\boxed{\ \ け\ \ }$の選択肢:
$(\textrm{a})p \geqq \frac{1}{100} (\textrm{b})\frac{1}{200} \leqq p \lt \frac{1}{100} (\textrm{c})\frac{1}{500} \leqq p \lt \frac{1}{200}$
$(\textrm{d})\frac{1}{1000} \leqq p \lt \frac{1}{500} (\textrm{e})\frac{1}{2000} \leqq p \lt \frac{1}{1000} (\textrm{f})\frac{1}{5000} \leqq p \lt \frac{1}{2000}$
$(\textrm{g})\frac{1}{10000} \leqq p \lt \frac{1}{5000} (\textrm{h})p \lt \frac{1}{10000}$
2021上智大学理系過去問
【数Ⅱ】中高一貫校問題集3(論理・確率編)124:式と証明:二項定理:21¹⁰を400で割った余りを求めよ。

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
教材:
#TK数学#TK数学問題集3(論理・確率編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
21¹⁰を400で割った余りを求めよ。
この動画を見る
21¹⁰を400で割った余りを求めよ。
シンプルな良問!!
見掛け倒しの方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$(2+\sqrt3)^{x^2-2x+1}+(2-\sqrt3)^{x^2-2x-1}=$
$\dfrac{2}{2-\sqrt3}$
この動画を見る
これを解け.
$(2+\sqrt3)^{x^2-2x+1}+(2-\sqrt3)^{x^2-2x-1}=$
$\dfrac{2}{2-\sqrt3}$
ちょっとした方程式 x^e=e^x
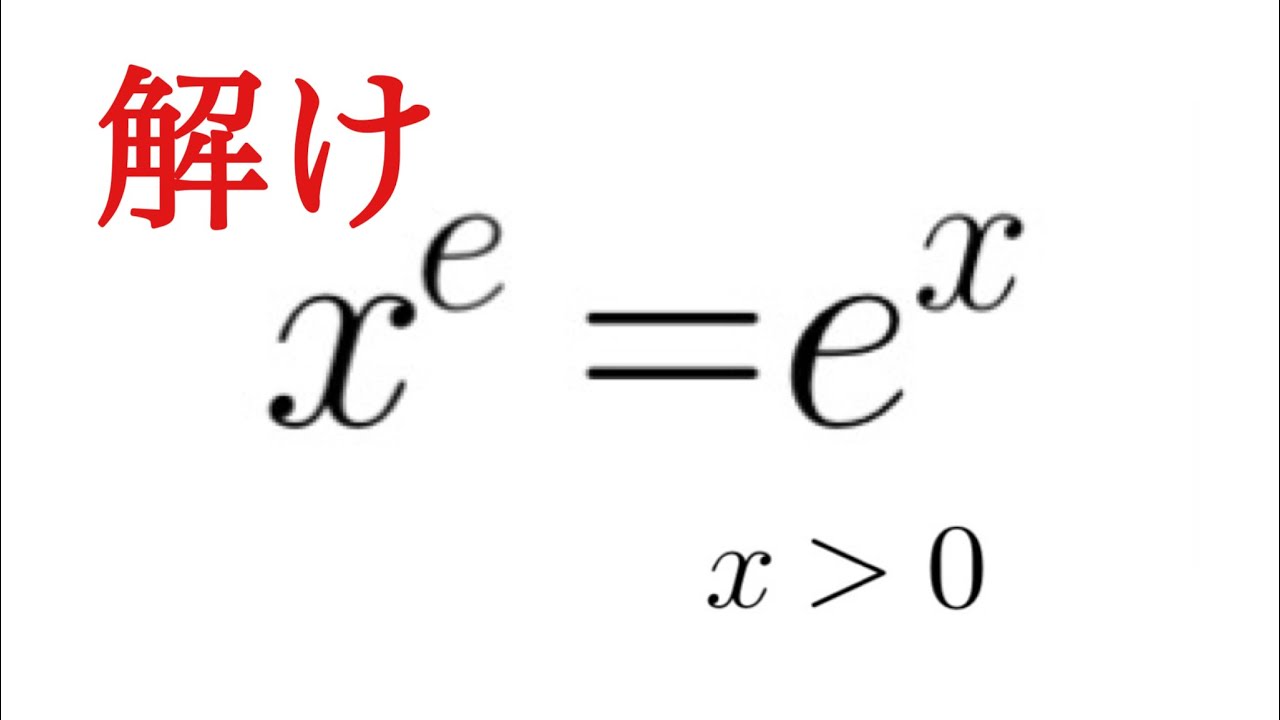
【数学】中高一貫校用問題集場合の数と確率:重複順列:9人を2つのグループに分ける。考え方は格付けチェック!?
単元:
#数A#場合の数と確率#場合の数#数学(高校生)
教材:
#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
9人を次のように分ける方法は通りあるか。
(1)2つのグループA、Bに分ける。ただし、各グループには少なくとも1人は入るものとする。
(2)2つのグループに分ける。
この動画を見る
9人を次のように分ける方法は通りあるか。
(1)2つのグループA、Bに分ける。ただし、各グループには少なくとも1人は入るものとする。
(2)2つのグループに分ける。
福田の数学〜上智大学2021年TEAP利用理系第1問(2)〜n進法

単元:
#計算と数の性質#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#規則性(周期算・方陣算・数列・日暦算・N進法)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(2)nを20以上の整数とする。n進法で表したとき、$n^3$の位の数が$1,n^2$の位の数が2,
$n^1$の位の数が$3,n^0$の位の数が0である数$1230_{(n)}$を$n+1$進法で表すと$(n+1)^2$の位
の数は$\boxed{\ \ あ\ \ }$であり、$(n+1)^1$の位の数は$\boxed{\ \ い\ \ }$であり、$(n+1)^0$の位の数は$\boxed{\ \ う\ \ }$である。
$\boxed{\ \ あ\ \ }\ ~\ \boxed{\ \ う\ \ }$の選択肢:
$(\textrm{a})0 (\textrm{b})1 (\textrm{c})2 (\textrm{d})3$
$(\textrm{e})n-2 (\textrm{f})n-3 (\textrm{g})n-1 (\textrm{g})n$
2021上智大学理系過去問
この動画を見る
${\Large\boxed{1}}$(2)nを20以上の整数とする。n進法で表したとき、$n^3$の位の数が$1,n^2$の位の数が2,
$n^1$の位の数が$3,n^0$の位の数が0である数$1230_{(n)}$を$n+1$進法で表すと$(n+1)^2$の位
の数は$\boxed{\ \ あ\ \ }$であり、$(n+1)^1$の位の数は$\boxed{\ \ い\ \ }$であり、$(n+1)^0$の位の数は$\boxed{\ \ う\ \ }$である。
$\boxed{\ \ あ\ \ }\ ~\ \boxed{\ \ う\ \ }$の選択肢:
$(\textrm{a})0 (\textrm{b})1 (\textrm{c})2 (\textrm{d})3$
$(\textrm{e})n-2 (\textrm{f})n-3 (\textrm{g})n-1 (\textrm{g})n$
2021上智大学理系過去問
【数A】中高一貫校問題集3(論理・確率編)86:場合の数と確率:重複順列:9人を2つのグループに分ける。考え方は格付けチェック!?
単元:
#数A#場合の数と確率#場合の数#数学(高校生)
教材:
#TK数学#TK数学問題集3(論理・確率編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
9人を次のように分ける方法は通りあるか。
(1)2つのグループA、Bに分ける。ただし、各グループには少なくとも1人は入るものとする。
(2)2つのグループに分ける。
この動画を見る
9人を次のように分ける方法は通りあるか。
(1)2つのグループA、Bに分ける。ただし、各グループには少なくとも1人は入るものとする。
(2)2つのグループに分ける。
福田の数学〜上智大学2021年TEAP利用理系第1問(1)〜偽陽性偽陰性の条件付き確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(1)ある病原菌の検査薬は、病原菌に感染しているのに誤って陰性と判断する
確率が20%、感染していないのに、誤って陽性と判断する確率が10%である。
全体の20%がこの病原菌に感染している集団から1つの検体を取り出して、
独立に2回、検査薬で検査する。こんとき、2回とも陰性であったが、実際には
感染している確率は$\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$であり、少なくとも1回は陽性であったが、
実際には病原菌には感染していない確率は$\frac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ エ\ \ }}$である。
2021上智大学理系過去問
この動画を見る
${\Large\boxed{1}}$(1)ある病原菌の検査薬は、病原菌に感染しているのに誤って陰性と判断する
確率が20%、感染していないのに、誤って陽性と判断する確率が10%である。
全体の20%がこの病原菌に感染している集団から1つの検体を取り出して、
独立に2回、検査薬で検査する。こんとき、2回とも陰性であったが、実際には
感染している確率は$\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$であり、少なくとも1回は陽性であったが、
実際には病原菌には感染していない確率は$\frac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ エ\ \ }}$である。
2021上智大学理系過去問
大学入試問題#3 慶應義塾大学(2021) 不等式を満たす整数の個数

単元:
#数A#整数の性質#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$x^2-5x+3-2log_3\ x \lt 0$を満たす自然数$x$の個数を求めよ。
出典:2021年慶應義塾大学 入試問題
この動画を見る
$x^2-5x+3-2log_3\ x \lt 0$を満たす自然数$x$の個数を求めよ。
出典:2021年慶應義塾大学 入試問題
神様の順列で瞬殺

単元:
#数A#場合の数と確率#確率#数列#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
52枚のトランプから1枚引いて見ないで伏せる.
残り51枚から3枚引いたら全部♡だった.
伏せた1枚が♡である確率を求めよ.
この動画を見る
52枚のトランプから1枚引いて見ないで伏せる.
残り51枚から3枚引いたら全部♡だった.
伏せた1枚が♡である確率を求めよ.
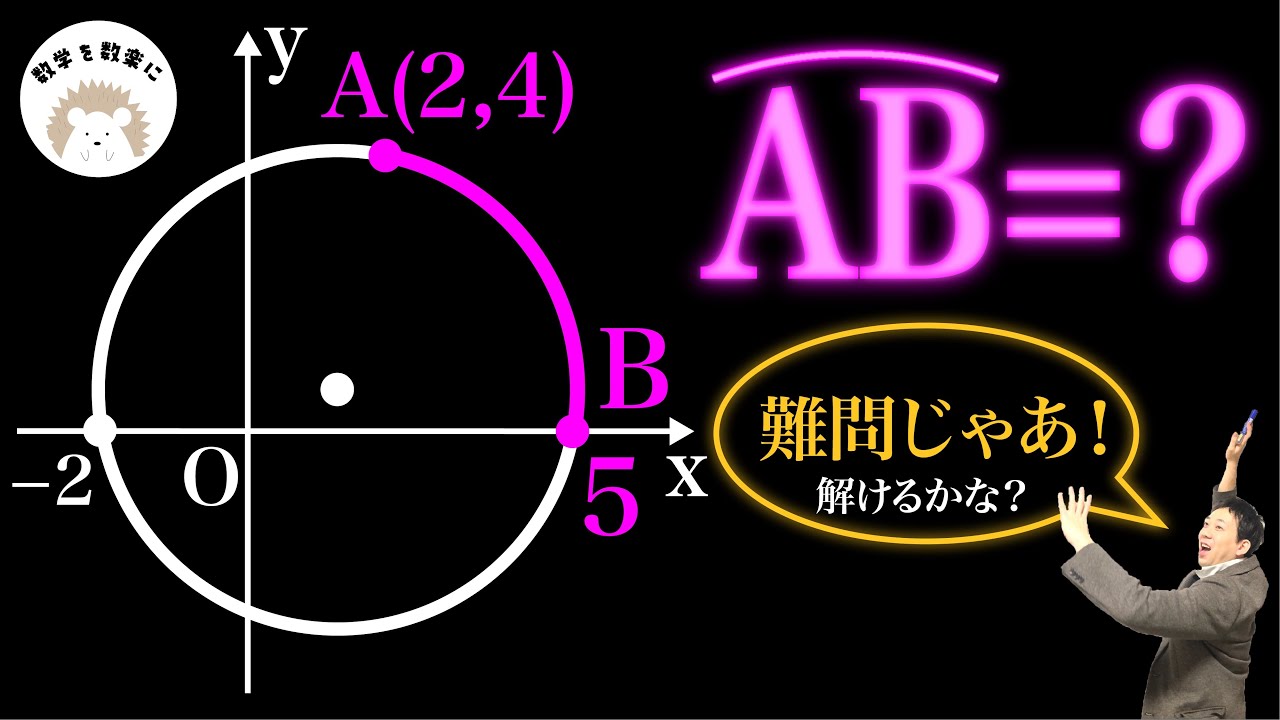
座標平面上の円 高校入試
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\overparen{AB}$=?
*図は動画内参照
この動画を見る
$\overparen{AB}$=?
*図は動画内参照
【平面図形の基礎はこれ!】三角形の性質の基礎編1〔高校数学 数学〕

福田の数学〜上智大学2021年TEAP利用文系第4問(1)〜条件の否定

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{4}}$(1)関数$f(x)$に対する以下の条件(P)を考える。
$(P): f(x) \gt 3$を満たす5以上の自然数nが存在する。
条件(P)の否定として正しいものを以下の選択肢からすべて選べ。
$(\textrm{a})f(n) \leqq 3$を満たす5以上の自然数nが存在する。
$(\textrm{b})f(n) \gt 3$を満たす5未満の自然数nが存在する。
$(\textrm{c})f(n) \leqq 3$を満たす5未満の自然数nが存在する。
$(\textrm{d})n$が5以上の自然数ならば$f(n) \leqq 3$が成り立つ。
$(\textrm{e})n$が5未満の自然数ならば$f(n) \leqq 3$が成り立つ。
$(\textrm{f})n$が5未満の自然数ならば$f(n) \gt 3$が成り立つ。
$(\textrm{g})f(n) \gt 3$が5以上の全ての自然数nに対して成り立つ。
$(\textrm{h})f(n) \leqq 3$が5以上の全ての自然数nに対して成り立つ。
$(\textrm{i})f(n) \leqq 3$が5未満の全ての自然数nに対して成り立つ。
2021上智大学文系過去問
この動画を見る
${\Large\boxed{4}}$(1)関数$f(x)$に対する以下の条件(P)を考える。
$(P): f(x) \gt 3$を満たす5以上の自然数nが存在する。
条件(P)の否定として正しいものを以下の選択肢からすべて選べ。
$(\textrm{a})f(n) \leqq 3$を満たす5以上の自然数nが存在する。
$(\textrm{b})f(n) \gt 3$を満たす5未満の自然数nが存在する。
$(\textrm{c})f(n) \leqq 3$を満たす5未満の自然数nが存在する。
$(\textrm{d})n$が5以上の自然数ならば$f(n) \leqq 3$が成り立つ。
$(\textrm{e})n$が5未満の自然数ならば$f(n) \leqq 3$が成り立つ。
$(\textrm{f})n$が5未満の自然数ならば$f(n) \gt 3$が成り立つ。
$(\textrm{g})f(n) \gt 3$が5以上の全ての自然数nに対して成り立つ。
$(\textrm{h})f(n) \leqq 3$が5以上の全ての自然数nに対して成り立つ。
$(\textrm{i})f(n) \leqq 3$が5未満の全ての自然数nに対して成り立つ。
2021上智大学文系過去問
福田の数学〜上智大学2021年TEAP利用文系第3問〜反復試行の確率と3次関数の極大値

単元:
#数A#数Ⅱ#大学入試過去問(数学)#場合の数と確率#確率#指数関数と対数関数#微分法と積分法#指数関数#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$硬貨を2枚投げる試行を3回繰り返して、1回目、2回目、3回目に出た表の枚数
を順に$\alpha,\beta,\gamma$とする。3次関数
$f(x)=(x-\alpha)(x-\beta)(x-\gamma)$
を考える。
(1)関数$y=f(x)$が極値をとらない確率は$\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}$である。
(2)関数$y=f(x)$が極大値をとるとき、その極大値の取り得る値のうち最小のもの
は$\boxed{\ \ ニ\ \ }$で、最大のものは$\frac{\boxed{\ \ ヌ\ \ }}{\boxed{\ \ ネ\ \ }}$である。
(3)関数$y=f(x)$が極大値$\boxed{\ \ ニ\ \ }$をとる確率は$\frac{\boxed{\ \ ノ\ \ }}{\boxed{\ \ ハ\ \ }}$である。
(4)関数$y=f(x)$が極大値$\frac{\boxed{\ \ ヌ\ \ }}{\boxed{\ \ ネ\ \ }}$を取る確率は$\frac{\boxed{\ \ ヒ\ \ }}{\boxed{\ \ フ\ \ }}$である。
2021上智大学文系過去問
この動画を見る
${\Large\boxed{3}}$硬貨を2枚投げる試行を3回繰り返して、1回目、2回目、3回目に出た表の枚数
を順に$\alpha,\beta,\gamma$とする。3次関数
$f(x)=(x-\alpha)(x-\beta)(x-\gamma)$
を考える。
(1)関数$y=f(x)$が極値をとらない確率は$\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}$である。
(2)関数$y=f(x)$が極大値をとるとき、その極大値の取り得る値のうち最小のもの
は$\boxed{\ \ ニ\ \ }$で、最大のものは$\frac{\boxed{\ \ ヌ\ \ }}{\boxed{\ \ ネ\ \ }}$である。
(3)関数$y=f(x)$が極大値$\boxed{\ \ ニ\ \ }$をとる確率は$\frac{\boxed{\ \ ノ\ \ }}{\boxed{\ \ ハ\ \ }}$である。
(4)関数$y=f(x)$が極大値$\frac{\boxed{\ \ ヌ\ \ }}{\boxed{\ \ ネ\ \ }}$を取る確率は$\frac{\boxed{\ \ ヒ\ \ }}{\boxed{\ \ フ\ \ }}$である。
2021上智大学文系過去問
【中学数学・数A】中高一貫校問題集2(代数編)267:確率と標本調査:確率の計算:5枚のカードを並べるときに両端や隣り合う場合の確率

単元:
#数学(中学生)#中2数学#数A#場合の数と確率#確率#確率#数学(高校生)
教材:
#TK数学#TK数学問題集2(代数編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
A,B,C,D,Eの文字が書かれたカードが1枚ずつある。このカードをよく混ぜて1列に並べるとき、次のような場合の確率を求めよう。
(1)Aが右端にくる。
(2)AとEが両端にくる。
(3)BとCが隣り合う。
この動画を見る
A,B,C,D,Eの文字が書かれたカードが1枚ずつある。このカードをよく混ぜて1列に並べるとき、次のような場合の確率を求めよう。
(1)Aが右端にくる。
(2)AとEが両端にくる。
(3)BとCが隣り合う。
【中学数学・数A】中高一貫校用問題集(代数編)確率と標本調査:確率の計算:5枚のカードを並べるときに両端や隣り合う場合の確率

単元:
#数学(中学生)#中3数学#数A#場合の数と確率#確率#標本調査#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
A,B,C,D,Eの文字が書かれたカードが1枚ずつある。このカードをよく混ぜて1列に並べるとき、次のような場合の確率を求めよう。
(1)Aが右端にくる。
(2)AとEが両端にくる。
(3)BとCが隣り合う。
この動画を見る
A,B,C,D,Eの文字が書かれたカードが1枚ずつある。このカードをよく混ぜて1列に並べるとき、次のような場合の確率を求めよう。
(1)Aが右端にくる。
(2)AとEが両端にくる。
(3)BとCが隣り合う。
PとCの違い分かる?

