 三角関数
三角関数
 三角関数
三角関数
三角関数 数Ⅱ三角関数の等式不等式応用【NI・SHI・NOがていねいに解説】
単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$0\leqq θ\lt 2π$のとき,次の方程式,不等式を解け。
(1)$2sin^2θ-3cosθ=0$
(2)$2cos^2θ-3sinθ-3=0$
(3)$2sin^2-\sqrt{3}sinθ\lt 0$
(4)$2sin^2θ-4<5cosθ$
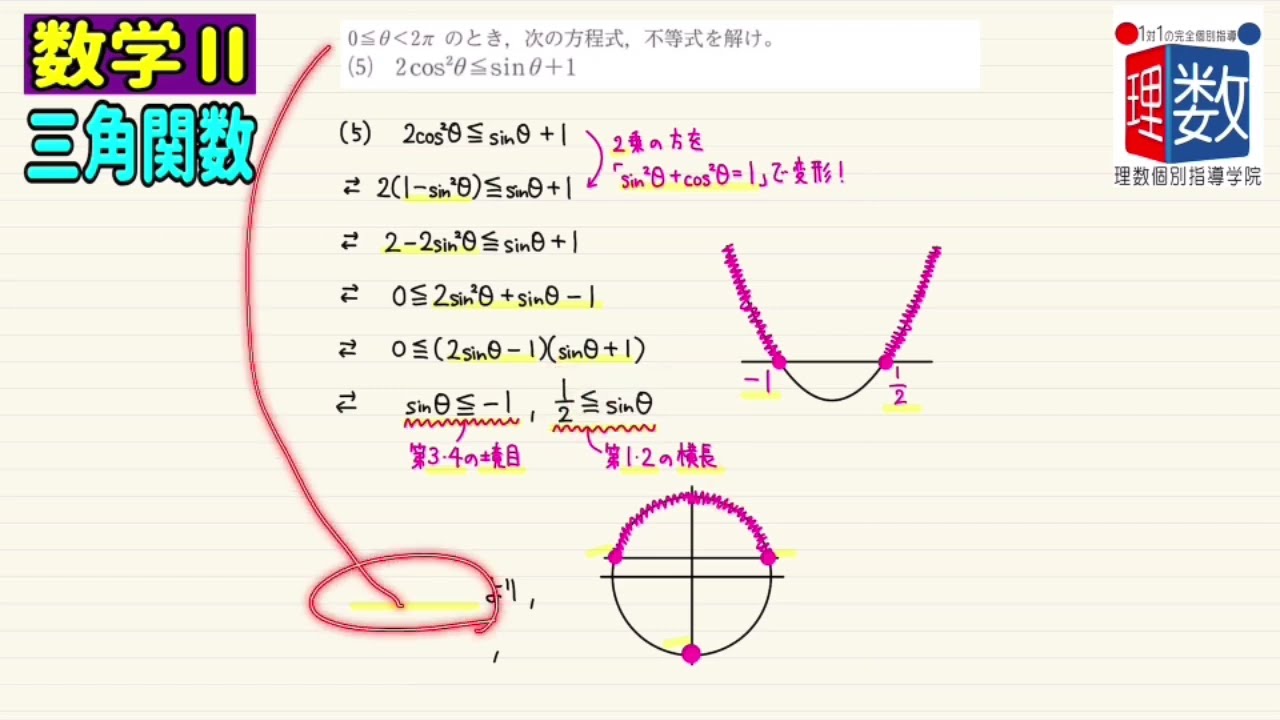
(5)$2cos²θ\leqq sinθ+1$
(6)$sinθ\lt tanθ$
この動画を見る
$0\leqq θ\lt 2π$のとき,次の方程式,不等式を解け。
(1)$2sin^2θ-3cosθ=0$
(2)$2cos^2θ-3sinθ-3=0$
(3)$2sin^2-\sqrt{3}sinθ\lt 0$
(4)$2sin^2θ-4<5cosθ$
(5)$2cos²θ\leqq sinθ+1$
(6)$sinθ\lt tanθ$
三角関数 数Ⅱ三角関数の最大値最小値2【NI・SHI・NOがていねいに解説】
単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
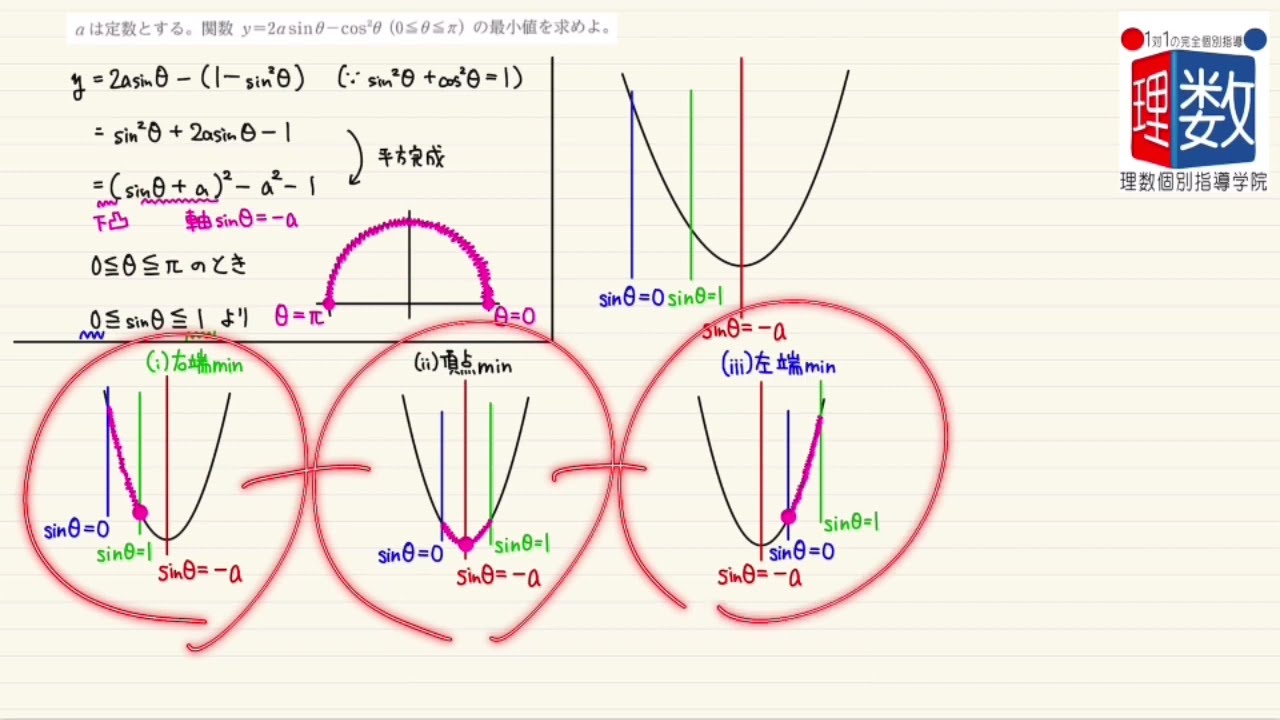
aは定数とする。関数$y=2asinθ-cos^2θ$ $(0≦θ≦π)$の最小値を求めよ。
この動画を見る
aは定数とする。関数$y=2asinθ-cos^2θ$ $(0≦θ≦π)$の最小値を求めよ。
三角関数 数Ⅱ三角関数の最大値最小値1【NI・SHI・NOがていねいに解説】

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数の最大値,最小値があれば,それを求めよ。また,そのときのθの値を求めよ。
(1) $y=\sin (θ-\displaystyle \frac{π}{3})$ $(0\leqq θ\leqq π)$
(2) $y=\tan (2θ-\displaystyle \frac{π}{4})$ $(0\leqq θ\leqq \displaystyle \frac{π}{4})$
(3) $y=\sin^2 θ-4\sin θ+1$ $(0\leqq θ\lt 2π)$
(4) $y=\sin^2 θ+\cos θ+1$ $(0\leqq θ\lt 2π)$
(5) $y=2\tan^2 θ+4\tan θ+5$ $(-\dfrac{π}{2}\lt θ\lt \dfrac{π}{2})$
この動画を見る
次の関数の最大値,最小値があれば,それを求めよ。また,そのときのθの値を求めよ。
(1) $y=\sin (θ-\displaystyle \frac{π}{3})$ $(0\leqq θ\leqq π)$
(2) $y=\tan (2θ-\displaystyle \frac{π}{4})$ $(0\leqq θ\leqq \displaystyle \frac{π}{4})$
(3) $y=\sin^2 θ-4\sin θ+1$ $(0\leqq θ\lt 2π)$
(4) $y=\sin^2 θ+\cos θ+1$ $(0\leqq θ\lt 2π)$
(5) $y=2\tan^2 θ+4\tan θ+5$ $(-\dfrac{π}{2}\lt θ\lt \dfrac{π}{2})$
三角関数 数Ⅱ三角関数の等式不等式(周期が変わる場合)【NI・SHI・NOがていねいに解説】
単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$0\leqq θ\lt 2π$のとき,次の不等式を解け。
(1) $\cos (2θ-\displaystyle \frac{π}{3})=\displaystyle \frac{1}{2}$
(2) $\sin (2θ+\displaystyle \frac{π}{6})=\displaystyle \frac{1}{\sqrt{2}}$
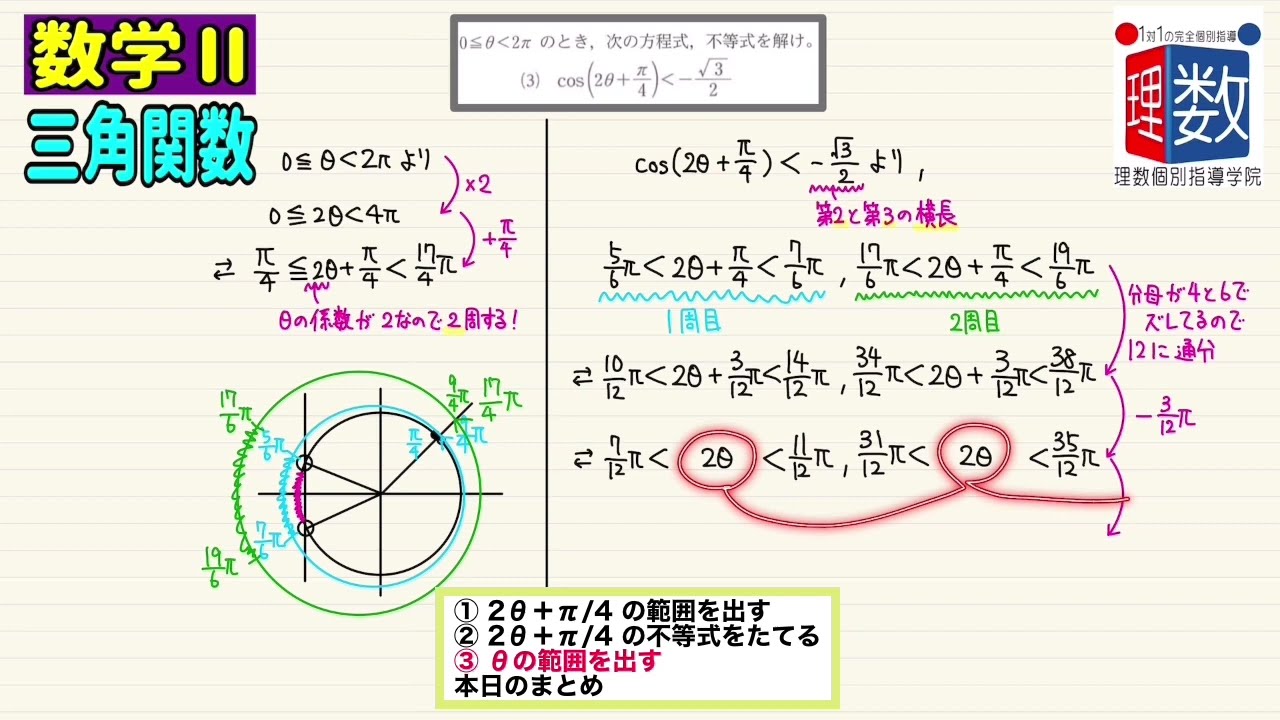
(3) $\cos (2θ+\displaystyle \frac{π}{4})\lt -\displaystyle \frac{\sqrt{3}}{2}$
(4) $\tan (2θ+\displaystyle \frac{π}{3})\geqq -\displaystyle \frac{1}{\sqrt{3}}$
この動画を見る
$0\leqq θ\lt 2π$のとき,次の不等式を解け。
(1) $\cos (2θ-\displaystyle \frac{π}{3})=\displaystyle \frac{1}{2}$
(2) $\sin (2θ+\displaystyle \frac{π}{6})=\displaystyle \frac{1}{\sqrt{2}}$
(3) $\cos (2θ+\displaystyle \frac{π}{4})\lt -\displaystyle \frac{\sqrt{3}}{2}$
(4) $\tan (2θ+\displaystyle \frac{π}{3})\geqq -\displaystyle \frac{1}{\sqrt{3}}$
三角関数 数 三角関数の不等式2【NI・SHI・NOがていねいに解説】
単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$0\leqq θ\lt 2π$のとき,次の不等式を解け。
(1) $\sin (θ+\displaystyle \frac{π}{4})\leqq \displaystyle \frac{\sqrt{3}}{2}$
(2) $\tan (θ-\displaystyle \frac{π}{6})\gt 1$
(3) $\cos (θ-\displaystyle \frac{π}{3})\lt -\displaystyle \frac{\sqrt{3}}{2}$
(4) $\tan (θ+\displaystyle \frac{π}{6})\geqq -\sqrt{3}$
この動画を見る
$0\leqq θ\lt 2π$のとき,次の不等式を解け。
(1) $\sin (θ+\displaystyle \frac{π}{4})\leqq \displaystyle \frac{\sqrt{3}}{2}$
(2) $\tan (θ-\displaystyle \frac{π}{6})\gt 1$
(3) $\cos (θ-\displaystyle \frac{π}{3})\lt -\displaystyle \frac{\sqrt{3}}{2}$
(4) $\tan (θ+\displaystyle \frac{π}{6})\geqq -\sqrt{3}$
三角関数 数Ⅱ三角関数の方程式【NI・SHI・NOがていねいに解説】

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
0≦θ<2πのとき,次の方程式を解け。
(1) $\sin (θ-\displaystyle \frac{π}{3})=-\displaystyle \frac{\sqrt{3}}{2}$
(2) $\cos (θ+\displaystyle \frac{π}{6})=\displaystyle \frac{1}{\sqrt{2}}$
(3) $\tan (θ+\displaystyle \frac{π}{4})=\displaystyle \frac{1}{\sqrt{3}}$
(4) $\cos (θ-\displaystyle \frac{π}{6})=-1$
この動画を見る
0≦θ<2πのとき,次の方程式を解け。
(1) $\sin (θ-\displaystyle \frac{π}{3})=-\displaystyle \frac{\sqrt{3}}{2}$
(2) $\cos (θ+\displaystyle \frac{π}{6})=\displaystyle \frac{1}{\sqrt{2}}$
(3) $\tan (θ+\displaystyle \frac{π}{4})=\displaystyle \frac{1}{\sqrt{3}}$
(4) $\cos (θ-\displaystyle \frac{π}{6})=-1$
三角関数 数Ⅱ 三角関数の不等式【NI・SHI・NOがていねいに解説】
単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
θの範囲に制限がないとき,次の不等式を解け。
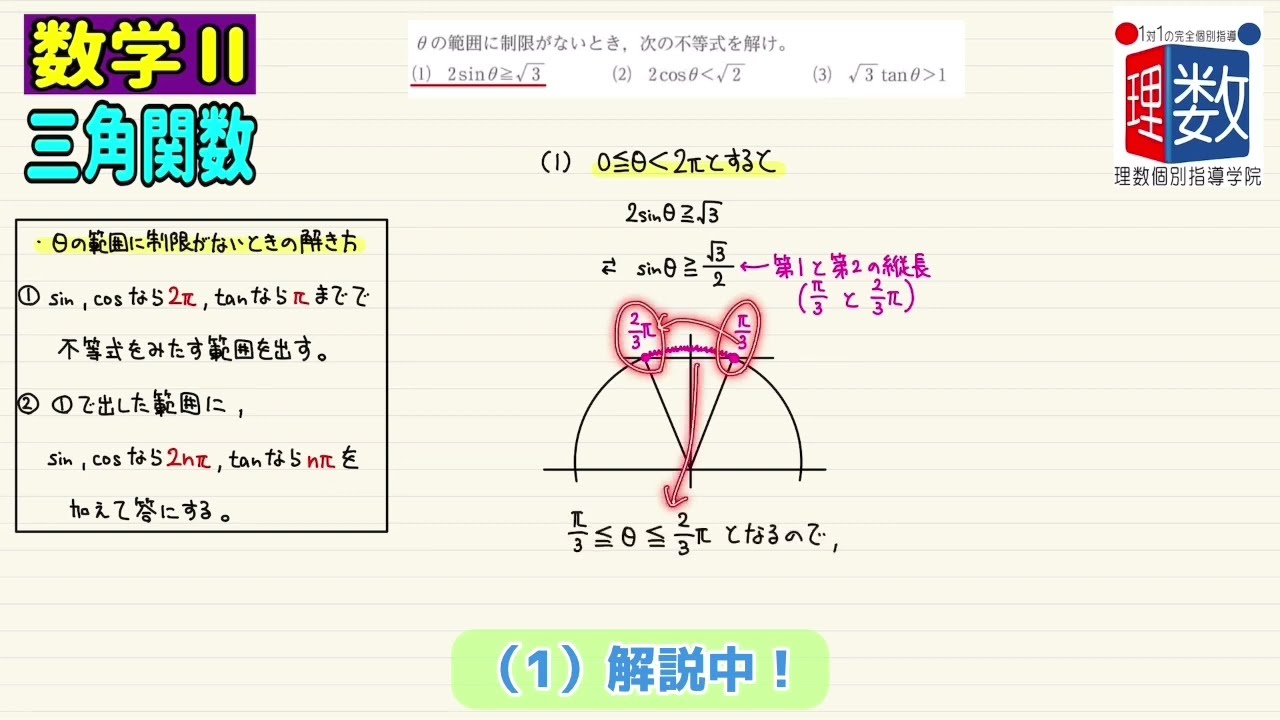
(1) $2sinθ≧\sqrt{3}$
(2) $2cosθ<√2$
(3) $\sqrt{3}tanθ>1$
この動画を見る
θの範囲に制限がないとき,次の不等式を解け。
(1) $2sinθ≧\sqrt{3}$
(2) $2cosθ<√2$
(3) $\sqrt{3}tanθ>1$
【高校数学】三角関数のグラフの書き方③【実践編】【NI・SHI・NOがていねいに解説】

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数の周期を求めよ。また,そのグラフをかけ。
(3) y=2sin(2θ+π/3)+1
『【高校数学】三角関数のグラフの書き方⓪【導入編】【NI・SHI・NOがていねいに解説】』https://youtu.be/ImaixQIXPKgを見てからこの動画は見てね!
この動画を見る
次の関数の周期を求めよ。また,そのグラフをかけ。
(3) y=2sin(2θ+π/3)+1
『【高校数学】三角関数のグラフの書き方⓪【導入編】【NI・SHI・NOがていねいに解説】』https://youtu.be/ImaixQIXPKgを見てからこの動画は見てね!
【高校数学】三角関数のグラフの書き方②【実践編】【NI・SHI・NOがていねいに解説】

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数の周期を求めよ。また,そのグラフをかけ。
(2) y=tan(θ/2-π/3)
『【高校数学】三角関数のグラフの書き方⓪【導入編】【NI・SHI・NOがていねいに解説】』https://youtu.be/ImaixQIXPKgを見てからこの動画は見てね!
この動画を見る
次の関数の周期を求めよ。また,そのグラフをかけ。
(2) y=tan(θ/2-π/3)
『【高校数学】三角関数のグラフの書き方⓪【導入編】【NI・SHI・NOがていねいに解説】』https://youtu.be/ImaixQIXPKgを見てからこの動画は見てね!
【高校数学】三角関数のグラフの書き方①【実践編】【NI・SHI・NOがていねいに解説】

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数の周期を求めよ。また,そのグラフをかけ。
(1) y=cos(3θ-π/2)
『【高校数学】三角関数のグラフの書き方⓪【導入編】【NI・SHI・NOがていねいに解説】』https://youtu.be/ImaixQIXPKgを見てからこの動画は見てね!
この動画を見る
次の関数の周期を求めよ。また,そのグラフをかけ。
(1) y=cos(3θ-π/2)
『【高校数学】三角関数のグラフの書き方⓪【導入編】【NI・SHI・NOがていねいに解説】』https://youtu.be/ImaixQIXPKgを見てからこの動画は見てね!
【高校数学】三角関数のグラフの書き方⓪【導入編】【NI・SHI・NOがていねいに解説】

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
三角関数(sin,cos,tan)のグラフの書き方を徹底解説!周期、基本の形から確認!
この動画を見る
三角関数(sin,cos,tan)のグラフの書き方を徹底解説!周期、基本の形から確認!
数Ⅲ頻出問題!確実に取れるようになっておこう!【京都大学】【数学 入試問題】

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$\triangle$ABCは条件$\angle B$=2,$\angle A,BC$=1を満たす三角形のうちで
面積が最大のものであるとする。
このとき、$cos\angle B$を求めよ。
この動画を見る
$\triangle$ABCは条件$\angle B$=2,$\angle A,BC$=1を満たす三角形のうちで
面積が最大のものであるとする。
このとき、$cos\angle B$を求めよ。
福田の数学〜2直線のなす角はtanの加法定理〜慶應義塾大学2023年商学部第2問〜2直線のなす角と面積

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$a \gt 0,b \lt 0$とする。放物線C:$y=\dfrac{3}{2}x^2$上の点A(a,$\dfrac{3}{2}a^2$)と点B(b,$\dfrac{3}{2}b^2$)について、点Aと点Bにおける放物線の接線をそれぞれlとmで表し、その好転をPとする。
(1)lとmが直交するとき、交点Pのy座標は$-\dfrac{\fbox{ア}}{\fbox{イ}}$である。
(2)a=2で、$\angle APB=\dfrac{\pi}{4}$とする。このとき、bの値は$-\dfrac{\fbox{ウ}}{\fbox{エオ}}$である。
(3)b=-aで、$\angle APB=\dfrac{\pi}{3}$とする。この時、aの値は$\dfrac{\sqrt{\fbox{カ}}}{\fbox{キ}}$である。また、PAを半径、$\angle APB$を中心角として扇形PABが定まる。この扇形は放物線Cによって2つの図形に分割され、大きい図形の面積と小さい図形の面積の差は$\dfrac{\fbox{ク}}{\fbox{ケ}}\pi-\dfrac{\fbox{コ}\sqrt{\fbox{サ}}}{\fbox{シ}}$である。
この動画を見る
$a \gt 0,b \lt 0$とする。放物線C:$y=\dfrac{3}{2}x^2$上の点A(a,$\dfrac{3}{2}a^2$)と点B(b,$\dfrac{3}{2}b^2$)について、点Aと点Bにおける放物線の接線をそれぞれlとmで表し、その好転をPとする。
(1)lとmが直交するとき、交点Pのy座標は$-\dfrac{\fbox{ア}}{\fbox{イ}}$である。
(2)a=2で、$\angle APB=\dfrac{\pi}{4}$とする。このとき、bの値は$-\dfrac{\fbox{ウ}}{\fbox{エオ}}$である。
(3)b=-aで、$\angle APB=\dfrac{\pi}{3}$とする。この時、aの値は$\dfrac{\sqrt{\fbox{カ}}}{\fbox{キ}}$である。また、PAを半径、$\angle APB$を中心角として扇形PABが定まる。この扇形は放物線Cによって2つの図形に分割され、大きい図形の面積と小さい図形の面積の差は$\dfrac{\fbox{ク}}{\fbox{ケ}}\pi-\dfrac{\fbox{コ}\sqrt{\fbox{サ}}}{\fbox{シ}}$である。
【FULL】定期テスト直前対策!図形と計量、三角関数解説動画フルパック流し【数I,数II】

単元:
#数Ⅰ#数Ⅱ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#三角関数#三角関数とグラフ#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
図形と計量、三角関数のまとめ動画です。
三角比の基本から、三角関数の和積や合成まで
見たい内容のシーンをチャプターから選んで下さい!!
この動画を見る
図形と計量、三角関数のまとめ動画です。
三角比の基本から、三角関数の和積や合成まで
見たい内容のシーンをチャプターから選んで下さい!!
【短時間でポイントチェック!!】三角関数の合成〔現役講師解説、数学〕

単元:
#数Ⅱ#三角関数#三角関数とグラフ#加法定理とその応用#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
$r \sin(\theta+\alpha)$の形に表せ。
ただし、$r>0,-\pi<\alpha≦\pi$とする。
①$\sin\theta-\cos\theta$
②$\frac{\sqrt{3}}{2}\sin\theta+\frac{1}{2}\cos\theta$
この動画を見る
$r \sin(\theta+\alpha)$の形に表せ。
ただし、$r>0,-\pi<\alpha≦\pi$とする。
①$\sin\theta-\cos\theta$
②$\frac{\sqrt{3}}{2}\sin\theta+\frac{1}{2}\cos\theta$
【短時間でポイントチェック!!】半角の公式〔現役講師解説、数学〕

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
$\frac{\pi}{2}<\theta<\pi$で$\sin\theta=\frac{1}{3}$のとき$\cos\frac{\theta}{2}$は?
この動画を見る
$\frac{\pi}{2}<\theta<\pi$で$\sin\theta=\frac{1}{3}$のとき$\cos\frac{\theta}{2}$は?
三角関数 数Ⅱ三角関数のグラフ2 三角関数8つの式をいちいち変形してたら面倒!裏ワザで秒で解説!【NI・SHI・NOがていねいに解説】

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
下の三角関数①~⑧のうち,グラフが図のようになるものをすべて選べ。(図は動画内参照)
①$y=\sin (θ+\frac{2π}{3}) $
② $y=\cos (θ+\frac{5π}{3}) $
③ $y=\sin (-θ+\frac{4π}{3}) $
④ $y=-\cos (θ+\frac{2π}{3}) $
⑤ $y=-\sin (θ-\frac{π}{6}) $
⑥ $y=\cos (θ-\frac{5π}{3}) $
⑦ $y=-\sin (-θ-\frac{π}{6}) $
⑧ $y=-\cos (-θ+\frac{4π}{3}) $
この動画を見る
下の三角関数①~⑧のうち,グラフが図のようになるものをすべて選べ。(図は動画内参照)
①$y=\sin (θ+\frac{2π}{3}) $
② $y=\cos (θ+\frac{5π}{3}) $
③ $y=\sin (-θ+\frac{4π}{3}) $
④ $y=-\cos (θ+\frac{2π}{3}) $
⑤ $y=-\sin (θ-\frac{π}{6}) $
⑥ $y=\cos (θ-\frac{5π}{3}) $
⑦ $y=-\sin (-θ-\frac{π}{6}) $
⑧ $y=-\cos (-θ+\frac{4π}{3}) $
【短時間でポイントチェック!!】2倍角の公式〔現役講師解説、数学〕

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
$0<\alpha<\pi$で$\cos\alpha=-\frac{4}{5}$のとき、$\sin2\alpha,\cos2\alpha$は?
この動画を見る
$0<\alpha<\pi$で$\cos\alpha=-\frac{4}{5}$のとき、$\sin2\alpha,\cos2\alpha$は?
三角関数 数Ⅱ三角関数のグラフ【NI・SHI・NOがていねいに解説】

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
図は,関数y=2sin(aθ-b)のグラフである。a>0,0<b<2πのとき,a,bおよび図中の目盛りA,B,Cの値を求めよ。
※図は動画内参照
この動画を見る
図は,関数y=2sin(aθ-b)のグラフである。a>0,0<b<2πのとき,a,bおよび図中の目盛りA,B,Cの値を求めよ。
※図は動画内参照
三角関数 数Ⅱ三角関数の最大最小【NI・SHI・NOがていねいに解説】
単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
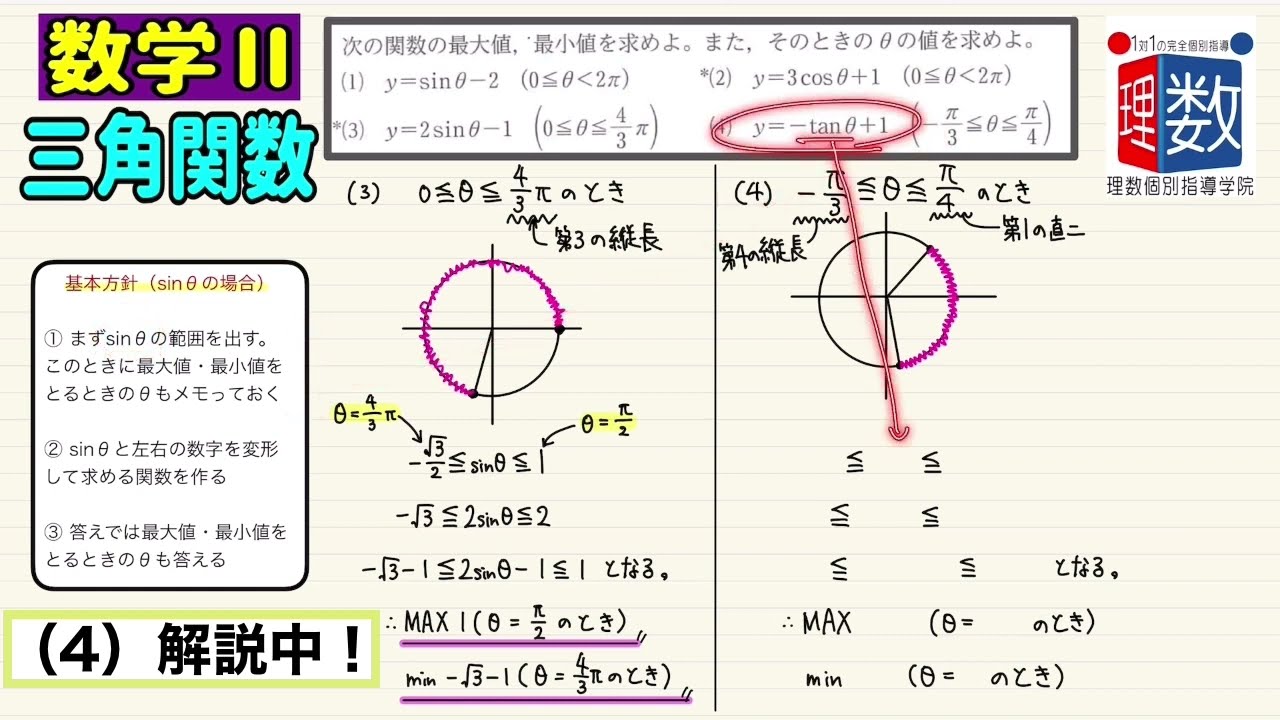
次の関数の最大値,最小値を求めよ。また,そのときのθの値を求めよ。
(1) $y=\sin θ-2 (0≦θ<2π)$
(2) $y=3\cos θ+1 (0≦θ<2π)$
(3) $y=2\sin θ-1 (0≦θ≦\frac{4π}{3})$
(4) $y=-\tan θ+1 (-\frac{π}{3}≦θ≦\frac{π}{4})$
この動画を見る
次の関数の最大値,最小値を求めよ。また,そのときのθの値を求めよ。
(1) $y=\sin θ-2 (0≦θ<2π)$
(2) $y=3\cos θ+1 (0≦θ<2π)$
(3) $y=2\sin θ-1 (0≦θ≦\frac{4π}{3})$
(4) $y=-\tan θ+1 (-\frac{π}{3}≦θ≦\frac{π}{4})$
気づけば一瞬!!!

三角関数 数Ⅱ三角比の変換【NI・SHI・NOがていねいに解説】
単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の式を簡単にせよ。
(1) $\cos θ+\cos ({θ+\frac{π}{2}})+\cos (θ+π)+\cos ({θ+\frac{3π}{2}})$
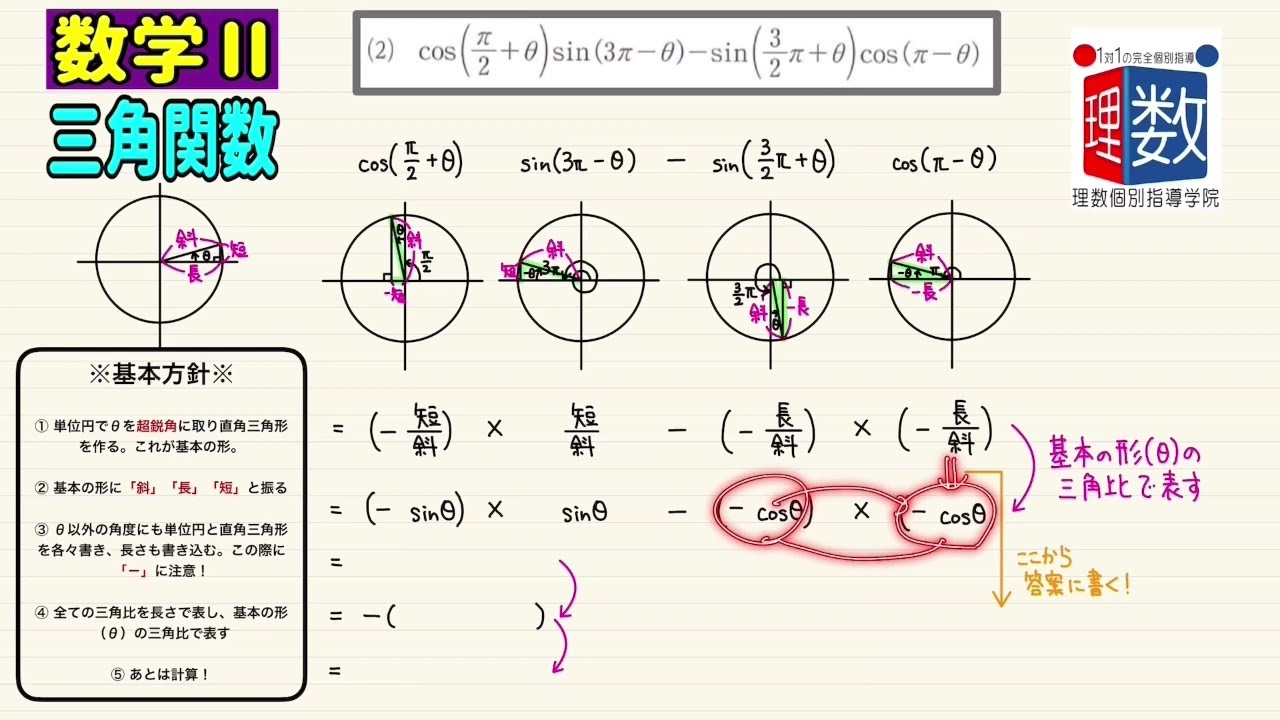
(2) $\cos ({\frac{π}{2}+θ})\sin (3π-θ) -\sin ({\frac{3π}{2}+θ})\cos (π-θ)$
この動画を見る
次の式を簡単にせよ。
(1) $\cos θ+\cos ({θ+\frac{π}{2}})+\cos (θ+π)+\cos ({θ+\frac{3π}{2}})$
(2) $\cos ({\frac{π}{2}+θ})\sin (3π-θ) -\sin ({\frac{3π}{2}+θ})\cos (π-θ)$
三角関数 数Ⅱ三角比の相互関係4【NI・SHI・NOがていねいに解説】

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$π \lt θ \lt \frac{3π}{2}$とする。
$\sin θ\cos θ=\frac{1}{4}$のとき,次の式の値を求めよ。
(1)$\sin θ+\cos θ$
(2)$\sin θ、\cos θ$
この動画を見る
$π \lt θ \lt \frac{3π}{2}$とする。
$\sin θ\cos θ=\frac{1}{4}$のとき,次の式の値を求めよ。
(1)$\sin θ+\cos θ$
(2)$\sin θ、\cos θ$
三角関数 数Ⅱ三角比の相互関係3【NI・SHI・NOがていねいに解説】

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$sinθ+cosθ=\frac{1}{2}$のとき,次の式の値を求めよ。
(1) $\tan θ+\displaystyle \frac{1}{\tan θ}$
(2) $\tan^3 θ+\displaystyle \frac{1}{\tan^3 θ}$
この動画を見る
$sinθ+cosθ=\frac{1}{2}$のとき,次の式の値を求めよ。
(1) $\tan θ+\displaystyle \frac{1}{\tan θ}$
(2) $\tan^3 θ+\displaystyle \frac{1}{\tan^3 θ}$
三角関数 数Ⅱ三角関数基本3【NI・SHI・NOがていねいに解説】
単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
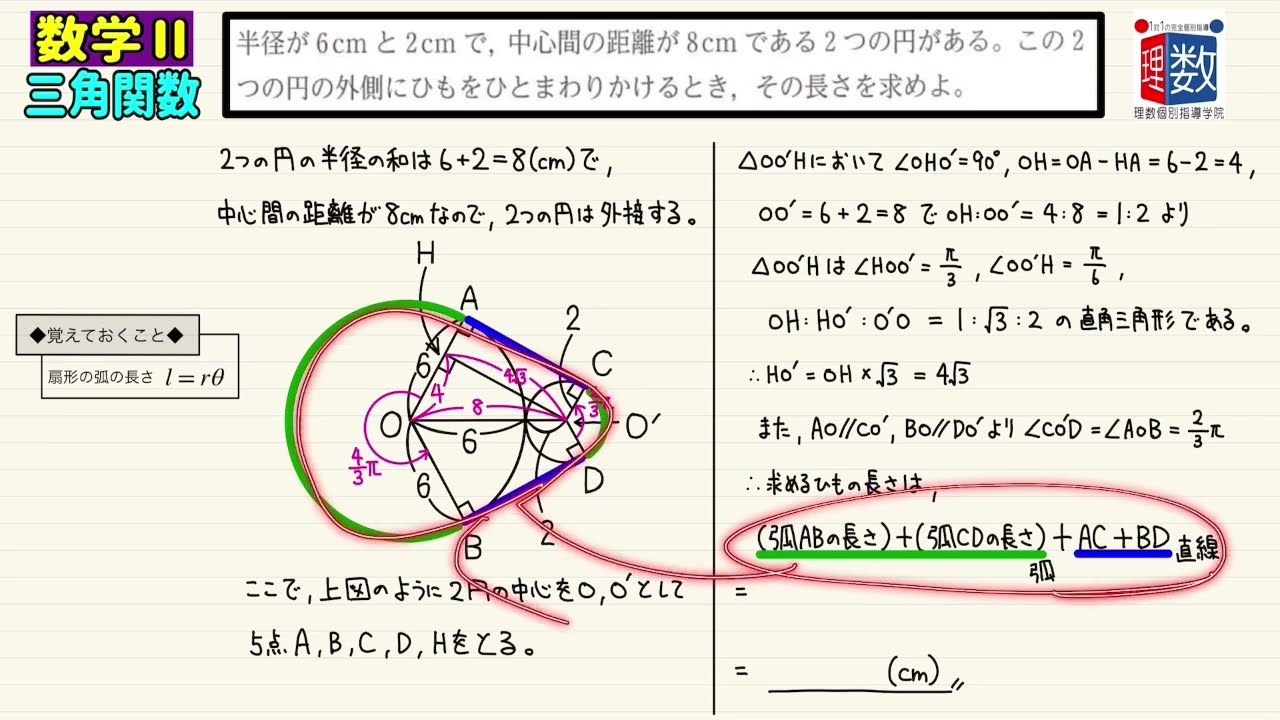
半径が6cmと2cmで,中心間の距離が8cmである2つの円がある。この2つの円の外側にひもをひとまわりかけるとき,その長さを求めよ。
この動画を見る
半径が6cmと2cmで,中心間の距離が8cmである2つの円がある。この2つの円の外側にひもをひとまわりかけるとき,その長さを求めよ。
三角関数 数Ⅱ三角比の相互関係2【NI・SHI・NOがていねいに解説】

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1) $tanθ=2$のとき,$\displaystyle \frac{1}{1+\sin θ}+\displaystyle \frac{1}{1-\sin θ}$の値を求めよ。
(2) $tanθ=5(0<θ<\frac{π}{2})$のとき,$\displaystyle \frac{1-\sin θ}{\cos θ}+\displaystyle \frac{\cos θ}{1-\sin θ}$の値を求めよ。
この動画を見る
(1) $tanθ=2$のとき,$\displaystyle \frac{1}{1+\sin θ}+\displaystyle \frac{1}{1-\sin θ}$の値を求めよ。
(2) $tanθ=5(0<θ<\frac{π}{2})$のとき,$\displaystyle \frac{1-\sin θ}{\cos θ}+\displaystyle \frac{\cos θ}{1-\sin θ}$の値を求めよ。
三角関数 数Ⅱ三角比の相互関係1【NI・SHI・NOがていねいに解説】

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の等式を証明せよ。
(1) $\displaystyle \frac{\sin^2 θ}{\tan^2 θ - \sin^2 θ}=\displaystyle \frac{1}{\tan^2 θ}$
(2) $(1+\sin θ+\cos θ)^2+(1+\sin θ-\cos θ)^2=4(1+\sin θ)$
(3) $\displaystyle \frac{\cos^2 θ-\sin^2 θ}{1+2\sin θ\cos θ}=\displaystyle \frac{1-\tan θ}{1+\tan θ}$
この動画を見る
次の等式を証明せよ。
(1) $\displaystyle \frac{\sin^2 θ}{\tan^2 θ - \sin^2 θ}=\displaystyle \frac{1}{\tan^2 θ}$
(2) $(1+\sin θ+\cos θ)^2+(1+\sin θ-\cos θ)^2=4(1+\sin θ)$
(3) $\displaystyle \frac{\cos^2 θ-\sin^2 θ}{1+2\sin θ\cos θ}=\displaystyle \frac{1-\tan θ}{1+\tan θ}$
三角関数 数Ⅱ三角関数基本2【NI・SHI・NOがていねいに解説】
単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
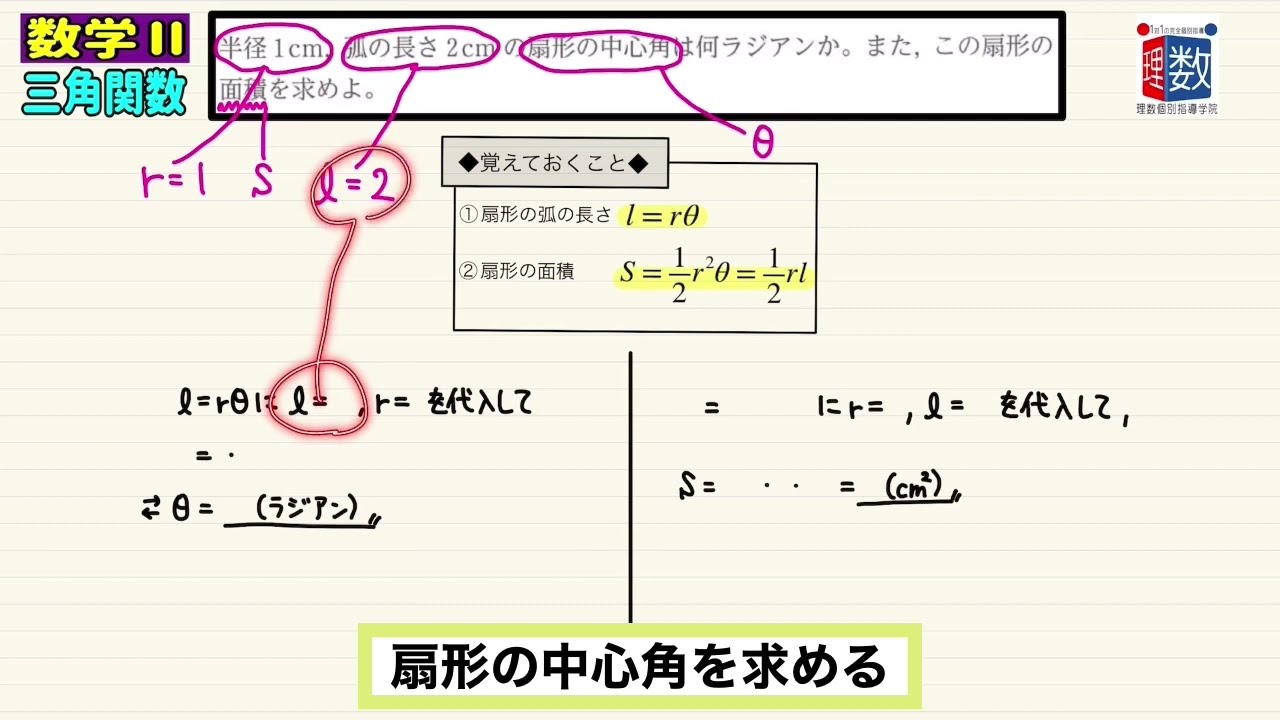
半径1cm,弧の長さ2cmの扇形の中心角は何ラジアンか。また,この扇形の面積を求めよ。
この動画を見る
半径1cm,弧の長さ2cmの扇形の中心角は何ラジアンか。また,この扇形の面積を求めよ。
三角関数 数Ⅱ三角関数基本1【NI・SHI・NOがていねいに解説】

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
座標平面上で,x軸の正の部分を始線にとる。角αの動径が第2象限にあり,角βの動径が第3象限にあるとき,次の角の動径は第何象限にあるか。ただし,2α,α+βの動径は,x軸上,y軸上にないものとする。
(1) 2α (2) α+β
この動画を見る
座標平面上で,x軸の正の部分を始線にとる。角αの動径が第2象限にあり,角βの動径が第3象限にあるとき,次の角の動径は第何象限にあるか。ただし,2α,α+βの動径は,x軸上,y軸上にないものとする。
(1) 2α (2) α+β
cosの和を求める

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\cos \dfrac{\pi}{7}-\cos \dfrac{2\pi}{7}+\cos \dfrac{3\pi}{7}$を求めよ
この動画を見る
$\cos \dfrac{\pi}{7}-\cos \dfrac{2\pi}{7}+\cos \dfrac{3\pi}{7}$を求めよ
