同志社高等学校
同志社高等学校
【使えるものは使え…！】整数：同志社高等学校～全国入試問題解法
単元：
#数学(中学生)#高校入試過去問(数学)#同志社高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
Nは十の位の数字がa,一の位の数字がbである2桁の自然数である.
MはNの十の位の数字と一の位の数字を入れ替えてできる自然数である.
$ N^2-M^2=693 $であるとき,自然数Nを求めよ.
同志社高等学校過去問
この動画を見る
Nは十の位の数字がa,一の位の数字がbである2桁の自然数である.
MはNの十の位の数字と一の位の数字を入れ替えてできる自然数である.
$ N^2-M^2=693 $であるとき,自然数Nを求めよ.
同志社高等学校過去問
【考え方が大切…！】確率：同志社高等学校～全国入試問題解法
単元：
#数学(中学生)#中２数学#確率#高校入試過去問(数学)#同志社高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
1から12までの整数から$ \color{red}{異なる3つ}$を選ぶ.
その$ \color{orange}{3つの数の積}$を$ \color{orange}{P}$とおく.
$ \color{orange}{P}$が$ \color{purple}{66の倍数}$であるとき,
3つの整数の選び方は,何通りあるか.
同志社高校過去問
この動画を見る
1から12までの整数から$ \color{red}{異なる3つ}$を選ぶ.
その$ \color{orange}{3つの数の積}$を$ \color{orange}{P}$とおく.
$ \color{orange}{P}$が$ \color{purple}{66の倍数}$であるとき,
3つの整数の選び方は,何通りあるか.
同志社高校過去問
【白板、爆破⁉】二次関数：同志社高等学校～全国入試問題解法【数楽】
単元：
#中３数学#2次関数#高校入試過去問(数学)#同志社高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$x$軸を回転の軸として $\triangle OAC$を1回転させて できる立体の体積を求めよ。
放物線:$ y = x^2$ 直線: $y = ax + b$ が2点$A$と$B$で交わる。
2点$A$、$B$を通る直線が、 $X$軸と交わる点をCとする。
この動画を見る
$x$軸を回転の軸として $\triangle OAC$を1回転させて できる立体の体積を求めよ。
放物線:$ y = x^2$ 直線: $y = ax + b$ が2点$A$と$B$で交わる。
2点$A$、$B$を通る直線が、 $X$軸と交わる点をCとする。
確率：同志社高等学校～全国入試問題解法【能研！】
単元：
#数学(中学生)#中２数学#確率#高校入試過去問(数学)#同志社高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
入試問題 同志社高等学校
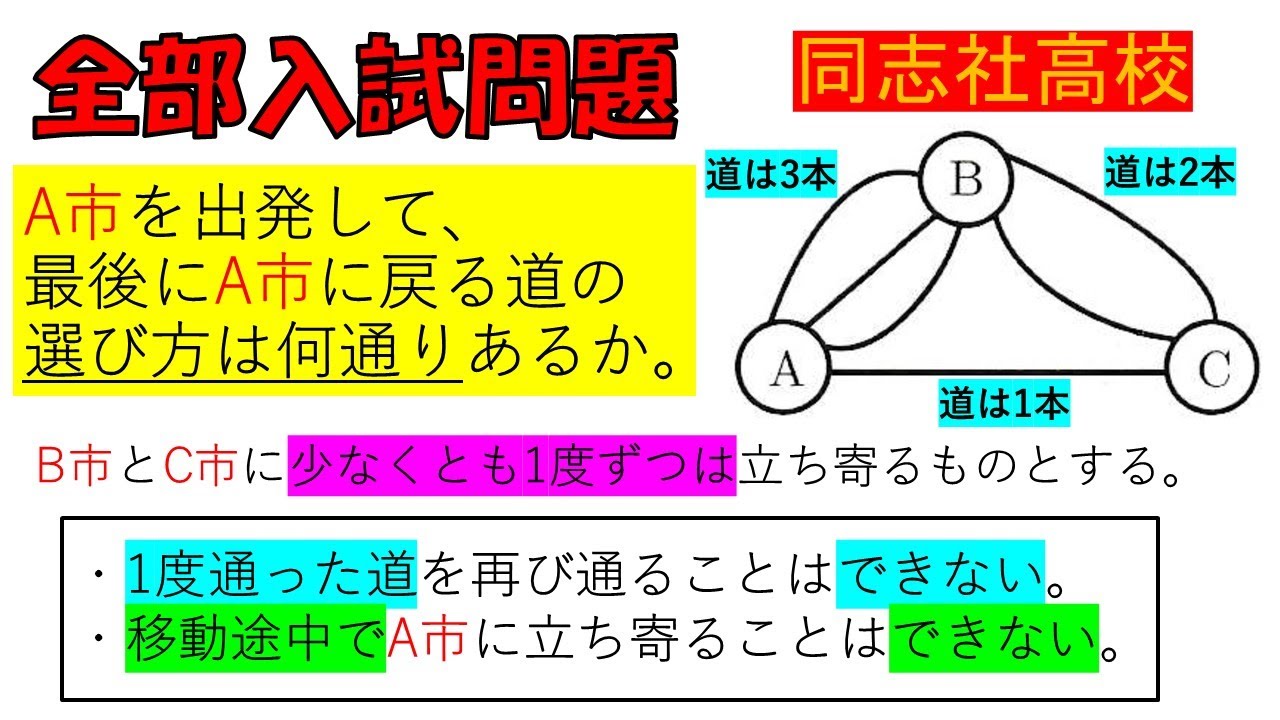
$A$市を出発して、 最後に$A$市に戻る道の 選び方は何通りあるか求めよ。
$B$市と$C$市に少なくとも1度ずつは立ち寄るものとする。
・1度通った道を再び通ることはできない。
・移動途中で$A$市に立ち寄ることはできない。
この動画を見る
入試問題 同志社高等学校
$A$市を出発して、 最後に$A$市に戻る道の 選び方は何通りあるか求めよ。
$B$市と$C$市に少なくとも1度ずつは立ち寄るものとする。
・1度通った道を再び通ることはできない。
・移動途中で$A$市に立ち寄ることはできない。