岐阜県公立高等学校
岐阜県公立高等学校
【入試らしい1問…！】図形：岐阜県～全国入試問題解法
単元：
#数学(中学生)#高校入試過去問(数学)#岐阜県公立高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$図1: 1辺9cmの立方体状の容器に水を入れる。→水面が頂点ABCを通る平面
$$図2: この容器を水平な台の上に置く。→底面から水面までの高さがxcmになった。$
この動画を見る
$図1: 1辺9cmの立方体状の容器に水を入れる。→水面が頂点ABCを通る平面
$$図2: この容器を水平な台の上に置く。→底面から水面までの高さがxcmになった。$
【重要な図形…！】図形：岐阜県～全国入試問題解法
単元：
#数学(中学生)#中１数学#中３数学#相似な図形#平面図形#高校入試過去問(数学)#岐阜県公立高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
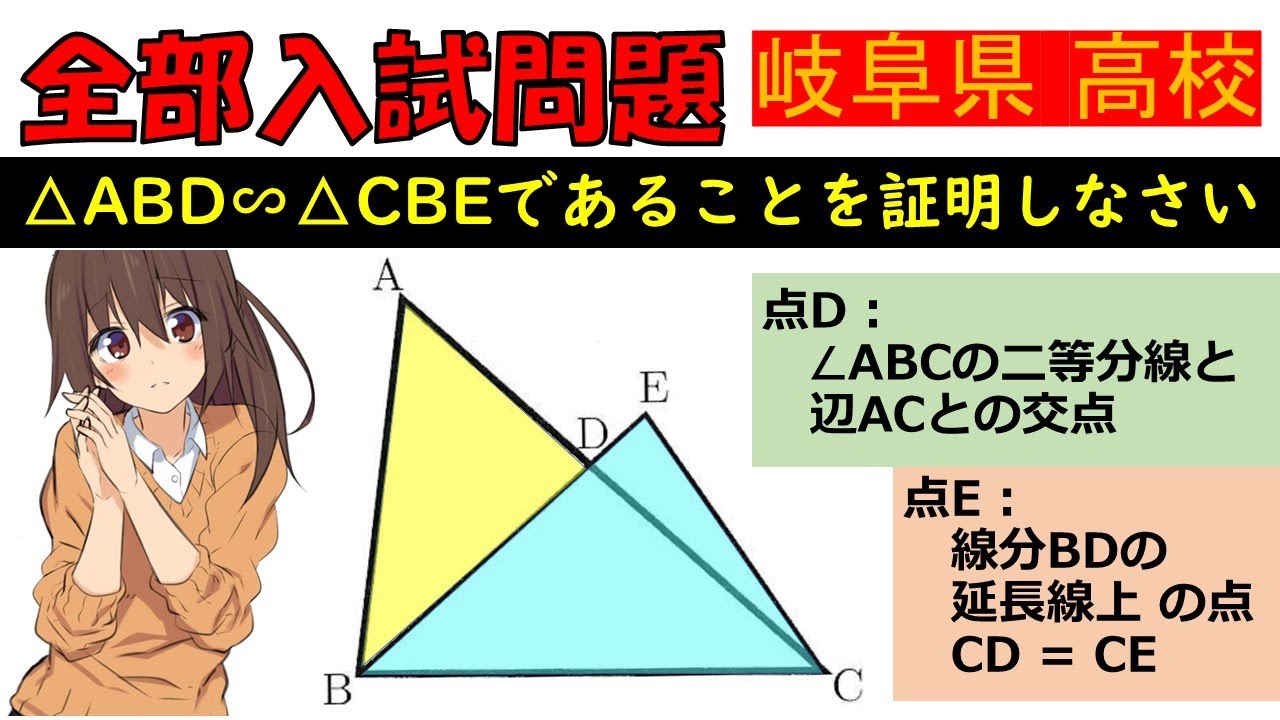
$\triangle ABD \backsim \triangle CBE であることを証明しなさい$
$点D : \angle ABCの二等分線と辺ACとの交点$
$点E : 線分BDの延長線上の点CD =CE$
この動画を見る
$\triangle ABD \backsim \triangle CBE であることを証明しなさい$
$点D : \angle ABCの二等分線と辺ACとの交点$
$点E : 線分BDの延長線上の点CD =CE$
【図形の奥義⁈実は追加の問題も大切！】図形：岐阜県立高等学校～全国入試問題解法
単元：
#数学(中学生)#高校入試過去問(数学)#岐阜県公立高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
全国入試問題～岐阜県立高等学校
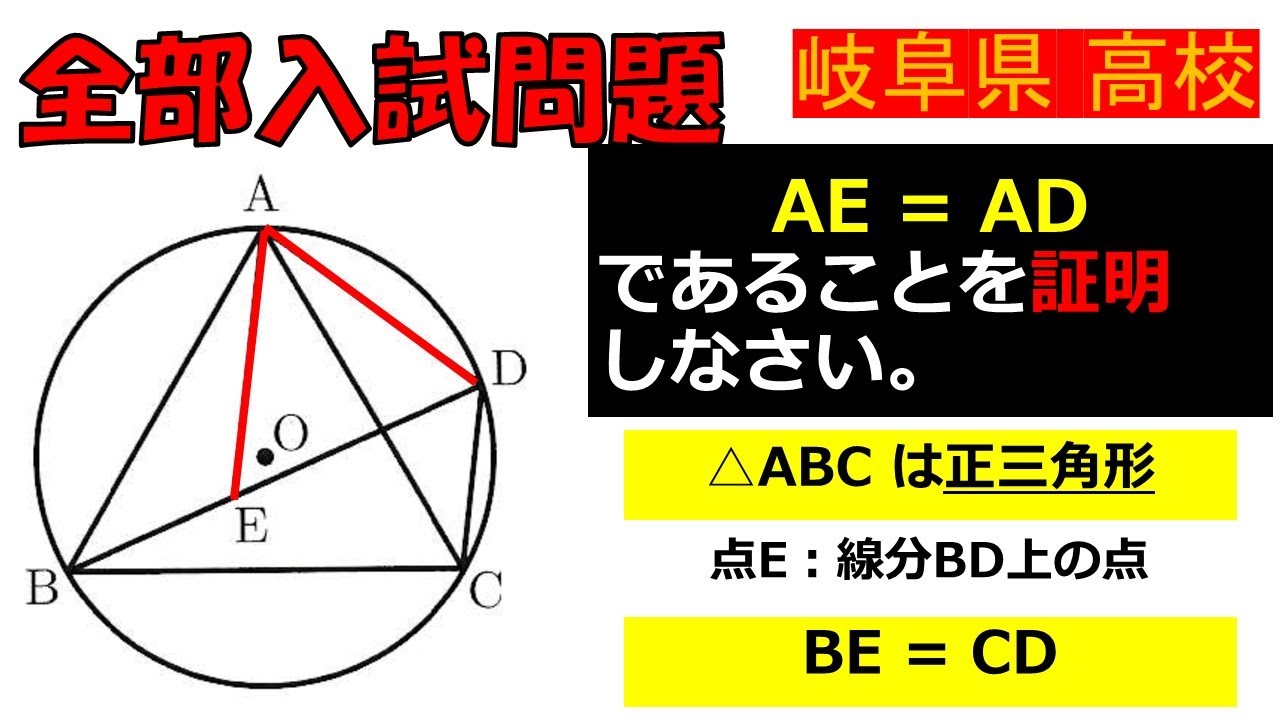
AE = ADであることを証明 しなさい。
△ABC は正三角形
点E:線分BD上の点
BE = CDは等しい
※図は動画内参照
この動画を見る
全国入試問題～岐阜県立高等学校
AE = ADであることを証明 しなさい。
△ABC は正三角形
点E:線分BD上の点
BE = CDは等しい
※図は動画内参照