久留米大学附設高等学校
久留米大学附設高等学校
【知ってる数字をどう活かすか！】文字式：久留米大学附設高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#高校入試過去問(数学)#久留米大学附設高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ x+7=7 $
$ x^2+y^2=169 $
を満たす$ x,y $について$ (x-y)(x^2-y^2)$の値を求めよ.
久留米大高校平野過去問
この動画を見る
$ x+7=7 $
$ x^2+y^2=169 $
を満たす$ x,y $について$ (x-y)(x^2-y^2)$の値を求めよ.
久留米大高校平野過去問
【まず、オーソドックスに正解を出そう！】文字式：久留米大学附設高等学校～全国入試問題解法
単元：
#数学(中学生)#高校入試過去問(数学)#久留米大学附設高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
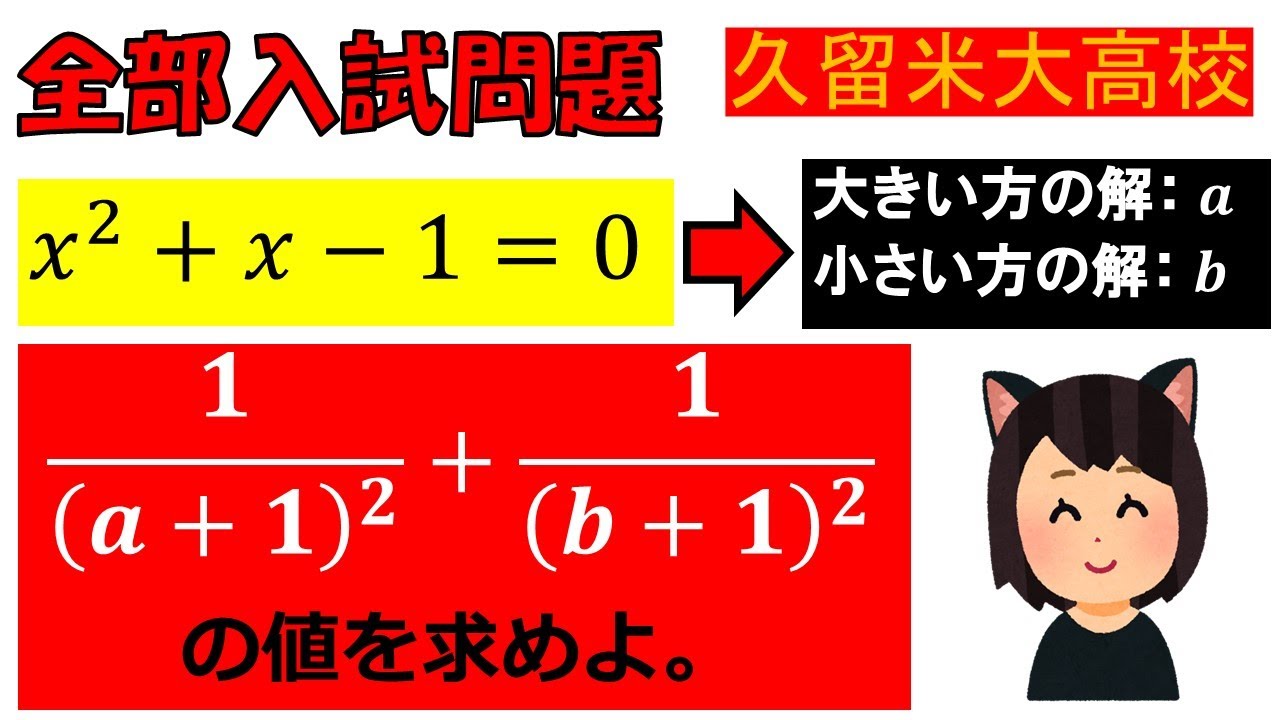
$x^2+x-1=0$
↓
大きいほうの解:a
小さいほうの解:b
$\displaystyle \frac{1}{(a+1)^2}+\displaystyle \frac{1}{(b+1)^2}$
の値を求めよ。
この動画を見る
$x^2+x-1=0$
↓
大きいほうの解:a
小さいほうの解:b
$\displaystyle \frac{1}{(a+1)^2}+\displaystyle \frac{1}{(b+1)^2}$
の値を求めよ。
【ケアレスミスをなくす3分間！】連立方程式：久留米大学附設高等学校～全部入試問題
単元：
#数学(中学生)#連立方程式#高校入試過去問(数学)#久留米大学附設高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
入試問題 久留米大学附設高等学校
【連立方程式】
aの値を求めよ。
$\begin{eqnarray}
\begin{cases}
8x-y=5 & \\
ax+5y=7 &
\end{cases}
\end{eqnarray}$
の解を$x=m,y=n$とするとき
$2m-n=1$が成り立つ
この動画を見る
入試問題 久留米大学附設高等学校
【連立方程式】
aの値を求めよ。
$\begin{eqnarray}
\begin{cases}
8x-y=5 & \\
ax+5y=7 &
\end{cases}
\end{eqnarray}$
の解を$x=m,y=n$とするとき
$2m-n=1$が成り立つ
【暗算!? 解けてスッキリ！】計算：久留米大学附設高等学校～全国入試問題解法
単元：
#中３数学#高校入試過去問(数学)#久留米大学附設高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
入試問題 久留米大附設高等学校
次の計算をせよ。
$\{(\displaystyle \frac{\sqrt{ 3 }}{\sqrt{ 2 }+1} ) ^2+ (\displaystyle \frac{\sqrt{ 3 }}{\sqrt{ 2 }-1} )^2\}^2-\{(\displaystyle \frac{\sqrt{ 3 }}{\sqrt{ 2 }+1} )^2 - (\displaystyle \frac{\sqrt{ 3 }}{\sqrt{ 2 }-1} )^2\}^2$
この動画を見る
入試問題 久留米大附設高等学校
次の計算をせよ。
$\{(\displaystyle \frac{\sqrt{ 3 }}{\sqrt{ 2 }+1} ) ^2+ (\displaystyle \frac{\sqrt{ 3 }}{\sqrt{ 2 }-1} )^2\}^2-\{(\displaystyle \frac{\sqrt{ 3 }}{\sqrt{ 2 }+1} )^2 - (\displaystyle \frac{\sqrt{ 3 }}{\sqrt{ 2 }-1} )^2\}^2$
文字式：久留米大学付属高等学校～全国入試問題解法
単元：
#数学(中学生)#式の計算（単項式・多項式・式の四則計算）#高校入試過去問(数学)#久留米大学附設高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
入試問題 久留米大学附属高等学校
$a=\sqrt{ 3 }+\sqrt{ 15 }$
$b=\sqrt{ 3 }-\sqrt{ 15 }$
のとき
→$\displaystyle \frac{a^2-ab+b^2}{a^2+ab+b^2}$
の値を求めよ。
この動画を見る
入試問題 久留米大学附属高等学校
$a=\sqrt{ 3 }+\sqrt{ 15 }$
$b=\sqrt{ 3 }-\sqrt{ 15 }$
のとき
→$\displaystyle \frac{a^2-ab+b^2}{a^2+ab+b^2}$
の値を求めよ。
【エナドリ！】連立方程式：久留米大学附設高等学校～全国入試問題解法
単元：
#数学(中学生)#中２数学#連立方程式#高校入試過去問(数学)#久留米大学附設高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
入試問題 久留米大学附設高等学校
次の問いに答えよ。
$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{1}{2x-3y}+\displaystyle \frac{2}{x+2y}=3 \\
\displaystyle \frac{3}{2x-3y}+\displaystyle \frac{2}{x+2y}=5
\end{array}
\right.
\end{eqnarray}$
連立方程式を解け。
この動画を見る
入試問題 久留米大学附設高等学校
次の問いに答えよ。
$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{1}{2x-3y}+\displaystyle \frac{2}{x+2y}=3 \\
\displaystyle \frac{3}{2x-3y}+\displaystyle \frac{2}{x+2y}=5
\end{array}
\right.
\end{eqnarray}$
連立方程式を解け。