 日本大学第三高等学校
日本大学第三高等学校
 日本大学第三高等学校
日本大学第三高等学校
【これなら分かる…!】図形:日本大学第三高等学校~全国入試問題解法
単元:
#算数(中学受験)#数学(中学生)#平面図形#平面図形その他#高校入試過去問(数学)#日本大学第三高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
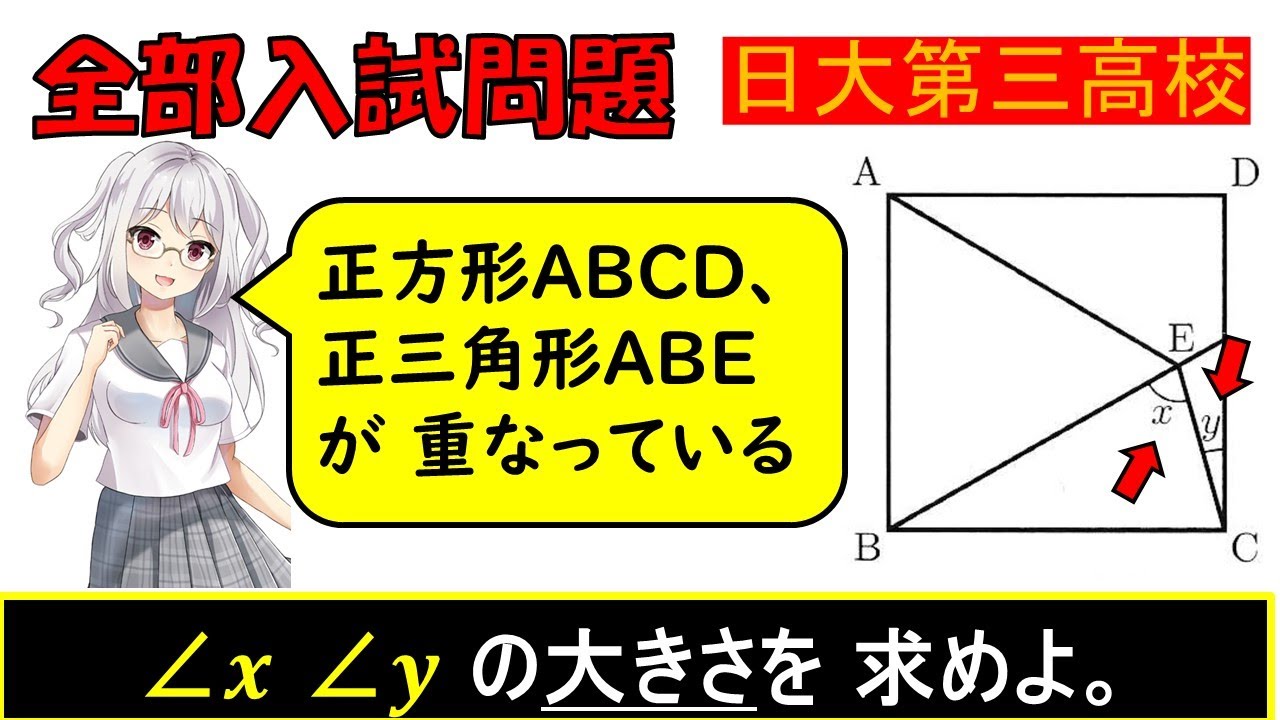
正方形ABCD、正三角形ABEが重なっている。角x,yの大きさを求めよ。
この動画を見る
正方形ABCD、正三角形ABEが重なっている。角x,yの大きさを求めよ。
【毎年どこかで…!】整数:日本大学第三高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#日本大学第三高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\sqrt{18(20-n)}$が整数となるような自然数$n$の値をすべて求めなさい
この動画を見る
$\sqrt{18(20-n)}$が整数となるような自然数$n$の値をすべて求めなさい
【分かる人が次に進む…!】二次関数:日本大学第三高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#日本大学第三高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
関数$ y=\dfrac{1}{2}x^2 $について
xの変域が$ a-3 \leqq x \leqq a+3$のとき,yの変域は$ b \leqq y \leqq 8$である.
*但し, $ -3 \lt a \lt 0 $
定数$ a,b $の値を求めなさい.
この動画を見る
関数$ y=\dfrac{1}{2}x^2 $について
xの変域が$ a-3 \leqq x \leqq a+3$のとき,yの変域は$ b \leqq y \leqq 8$である.
*但し, $ -3 \lt a \lt 0 $
定数$ a,b $の値を求めなさい.
二次関数:日本大学第三高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#日本大学第三高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 日本大学第三高等学校
放物線$y = ax^2 (a \gt 0)$ 上に$2$点$A$と$B$。
点$A:(-2,8)$
点$B:x$座標が$3$
点$C:$直線$AB$と$y$軸の交点
(1)$a$の値を求めなさい。
(2)直線$AB$の式を求めなさい。
この動画を見る
入試問題 日本大学第三高等学校
放物線$y = ax^2 (a \gt 0)$ 上に$2$点$A$と$B$。
点$A:(-2,8)$
点$B:x$座標が$3$
点$C:$直線$AB$と$y$軸の交点
(1)$a$の値を求めなさい。
(2)直線$AB$の式を求めなさい。
【条件を見定めて瞬殺!理解度チェック!】図形:日本大学第三高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#平面図形#高校入試過去問(数学)#日本大学第三高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
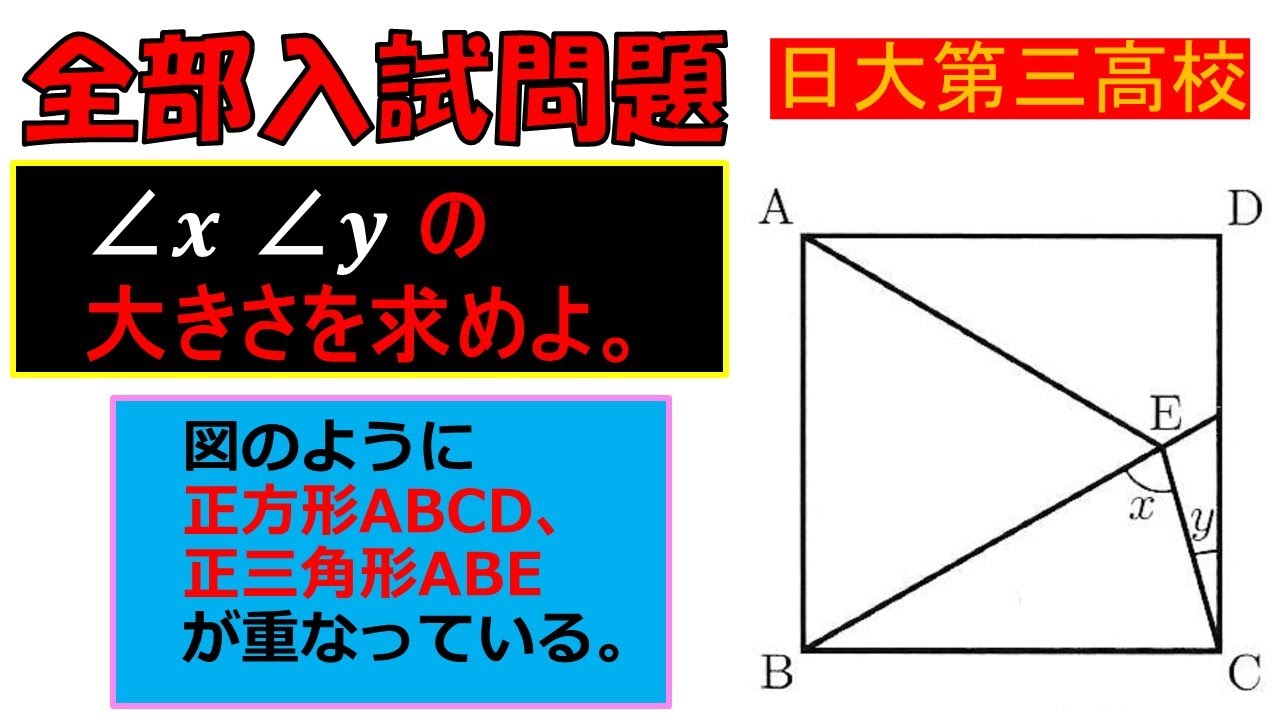
入試問題 日本大学第三高等学校
$\angle x \angle y$
の大きさを求めよ。
図のように 正方形ABCD、 正三角形ABE が重なっている。
※図は動画内参照
この動画を見る
入試問題 日本大学第三高等学校
$\angle x \angle y$
の大きさを求めよ。
図のように 正方形ABCD、 正三角形ABE が重なっている。
※図は動画内参照
【3分で身に付く考える力!】文字式:日本大学第三高等学校~全国入試問題解法

単元:
#数学(中学生)#文字と式#高校入試過去問(数学)#日本大学第三高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 日本大学第三高等学校
$(x+y)^2=\displaystyle \frac{51+10\sqrt{ 2 }}{5}$
のとき
$x-y=\displaystyle \frac{1-5\sqrt{ 2 }}{\sqrt{ 5 }}$
のとき
$4xy$の値を求めなさい。
この動画を見る
入試問題 日本大学第三高等学校
$(x+y)^2=\displaystyle \frac{51+10\sqrt{ 2 }}{5}$
のとき
$x-y=\displaystyle \frac{1-5\sqrt{ 2 }}{\sqrt{ 5 }}$
のとき
$4xy$の値を求めなさい。
