 文字と式
文字と式
 文字と式
文字と式
【学問に王道なし!】整数:福岡大学附属大濠高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)#福岡大学附属大濠高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ n $は正の整数であり, $ a,b,c,d $は整数である.
$ n=(a^2-1)(b^2-2)\times(c^2-3)(d^2-4)$
このような$ \color{red}{nの値}$で最小の値は$ \Box $である.
福岡大学附属大濠高等学校過去問
この動画を見る
$ n $は正の整数であり, $ a,b,c,d $は整数である.
$ n=(a^2-1)(b^2-2)\times(c^2-3)(d^2-4)$
このような$ \color{red}{nの値}$で最小の値は$ \Box $である.
福岡大学附属大濠高等学校過去問
高校入試の文字式の問題を15秒で解説~全国入試問題解法 #shorts #数学 #高校受験 #動体視力 #sound

単元:
#数学(中学生)#中1数学#文字と式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\color{red}{ x=4-\sqrt{2022}}$のとき,
$\color{orange}{x^2-8x+15}$の値を求めよ.
関西大倉高校過去問
この動画を見る
$\color{red}{ x=4-\sqrt{2022}}$のとき,
$\color{orange}{x^2-8x+15}$の値を求めよ.
関西大倉高校過去問
【題意を式で表せ!】整数:法政大学高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#方程式#文字と式#高校入試過去問(数学)#法政大学高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \color{red}{整数a}$を$ \color{red}{7}$で割ると$ \color{red}{4}$余り,$ \color{red}{整数b}$を$ \color{red}{7}$で割ると$ \color{red}{3}$余る.
$ \color{orange}{a^2+2ab}$を$ \color{orange}{7}$で割ったときの$ \color{orange}{余り}$を求めなさい.
法政大高校過去問
この動画を見る
$ \color{red}{整数a}$を$ \color{red}{7}$で割ると$ \color{red}{4}$余り,$ \color{red}{整数b}$を$ \color{red}{7}$で割ると$ \color{red}{3}$余る.
$ \color{orange}{a^2+2ab}$を$ \color{orange}{7}$で割ったときの$ \color{orange}{余り}$を求めなさい.
法政大高校過去問
【落ち着いて、そして、素早く!】文字式:奈良県公立高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)#奈良県公立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ a \lt o,b \lt 0 $のとき,
$ a+b,a-b,ab,\dfrac{a}{b}$のうちで,式の値が最も小さいものはどれか.
奈良県公立高等学校過去問
この動画を見る
$ a \lt o,b \lt 0 $のとき,
$ a+b,a-b,ab,\dfrac{a}{b}$のうちで,式の値が最も小さいものはどれか.
奈良県公立高等学校過去問
数学の文章題を解く流れをつかむ30秒~全国入試問題解法 #shorts #数学 #高校受験 #mathematics

単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)#精華女子高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
ある自然数を2乗して3引くところを間違えて2倍して3引いたので,
正しい答えより15小さくなった.ある自然数を求めよ.
精華女子高校過去問
この動画を見る
ある自然数を2乗して3引くところを間違えて2倍して3引いたので,
正しい答えより15小さくなった.ある自然数を求めよ.
精華女子高校過去問
【大切な基礎がここにある!】文字式:滋賀県高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)#滋賀県公立高校入試#滋賀県公立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ A=4x-1,B=-2x+3 $とするとき,次の式を計算しなさい.
$ -4A+3B+2A $
滋賀県高等学校過去問
この動画を見る
$ A=4x-1,B=-2x+3 $とするとき,次の式を計算しなさい.
$ -4A+3B+2A $
滋賀県高等学校過去問
約分して0!

帯分数と文字式
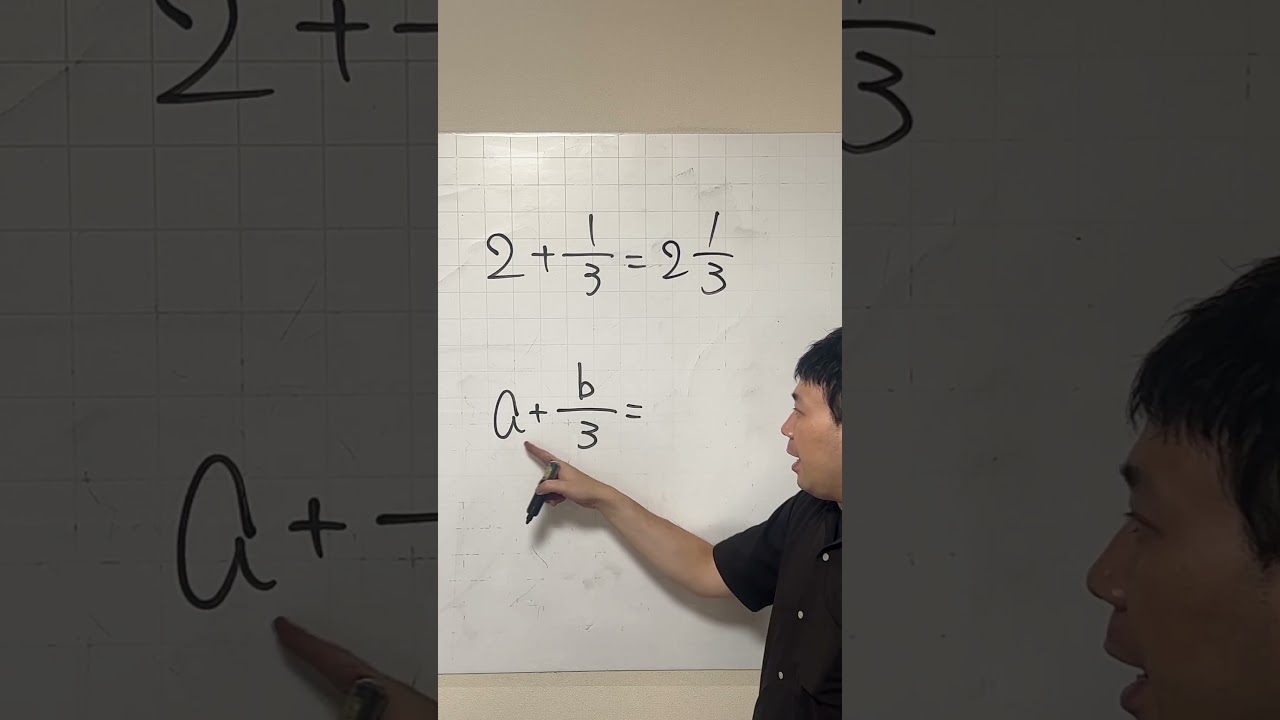
1はいちいち書くな
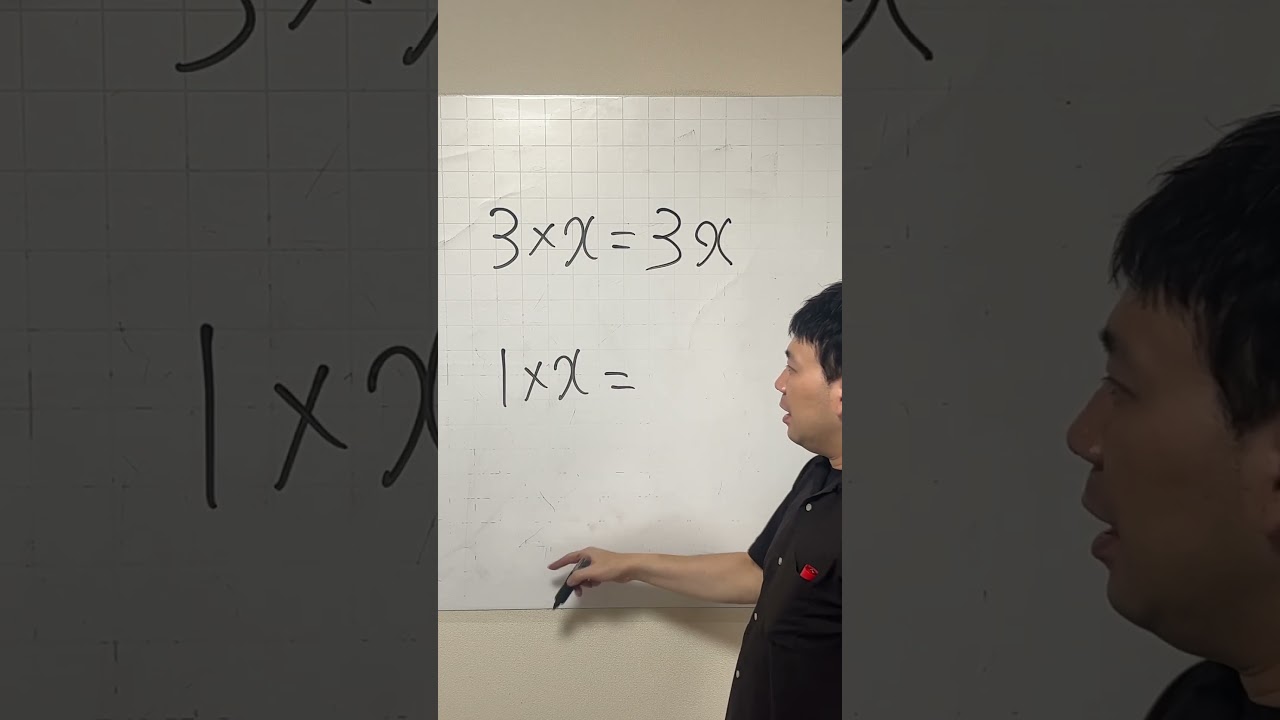
【まず自力で解こう!】文字式:成城学園高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#中3数学#平方根#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ x=2\sqrt3+2\sqrt2 $
$ y=\sqrt3-\sqrt2 $
のとき,$ x^2-4y^2 $の値を求めよ.
成蹊学園高校過去問
この動画を見る
$ x=2\sqrt3+2\sqrt2 $
$ y=\sqrt3-\sqrt2 $
のとき,$ x^2-4y^2 $の値を求めよ.
成蹊学園高校過去問
【考えすぎも悪くない…】文字式:興南高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ x+y=-5 $
$ x^2+y^2=17 $
のとき,$ xy $の値を求めなさい.
興南高校過去問
この動画を見る
$ x+y=-5 $
$ x^2+y^2=17 $
のとき,$ xy $の値を求めなさい.
興南高校過去問
8x=1の天才の解法がすごい...
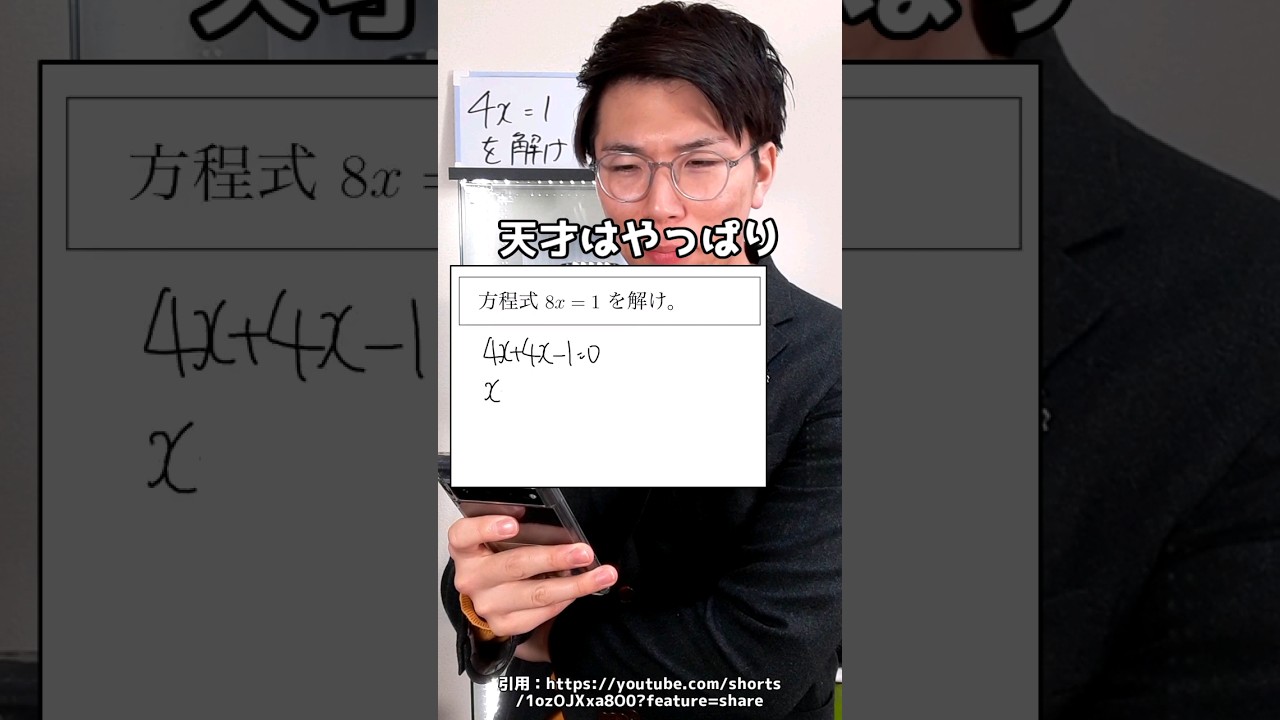
これなんでバツなん?

【中学数学】数学用語チェック絵本 中1の用語”せめて”これだけは覚えよう!!

単元:
#数学(中学生)#中1数学#正の数・負の数#方程式#比例・反比例#空間図形#資料の活用#文字と式#平面図形
指導講師:
理数個別チャンネル
問題文全文(内容文):
中1で登場する数学用語の中で、せめてこれだけは覚えてほしいものをピックアップ!vol.1~7の方も見てね♪
この動画を見る
中1で登場する数学用語の中で、せめてこれだけは覚えてほしいものをピックアップ!vol.1~7の方も見てね♪
小学校のまとめ、中学受験の基礎(キソ) 文字と式3/8

単元:
#数学(中学生)#中1数学#文字と式
指導講師:
算数・数学ちゃんねる
問題文全文(内容文):
小学校のまとめ、中学受験の基礎(キソ) 文字と式3/8
$□-27=3$
$x-9=45$
$□-99=1$
$□$/$x$を求めよ。
この動画を見る
小学校のまとめ、中学受験の基礎(キソ) 文字と式3/8
$□-27=3$
$x-9=45$
$□-99=1$
$□$/$x$を求めよ。
【考え方は大切、いろんな意味で】文字式:大阪星光学院高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ a=\dfrac{1}{\sqrt3+1}$
$ b=\dfrac{1}{\sqrt3-1}$のとき,$ a^3+a^2b+ab^2+b^3=\Box $である.
大阪星光高校過去問
この動画を見る
$ a=\dfrac{1}{\sqrt3+1}$
$ b=\dfrac{1}{\sqrt3-1}$のとき,$ a^3+a^2b+ab^2+b^3=\Box $である.
大阪星光高校過去問
【ケアレスミスをなくすには…!】計算:江戸川学園取手高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#正の数・負の数#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ -144a^4b^2c^3\div(-6a^3b^2c^2)^3\times \left(-\dfrac{3}{2}a^3b^2c\right)^2$を計算しなさい.
江戸川取手高校過去問
この動画を見る
$ -144a^4b^2c^3\div(-6a^3b^2c^2)^3\times \left(-\dfrac{3}{2}a^3b^2c\right)^2$を計算しなさい.
江戸川取手高校過去問
【条件から導き出されることは…!】整数:灘高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#整数の性質#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$x$を$x-n+a$と表す.
$ x^2+a^2=8$のとき,$n=\Box,x=\Box$である.
灘高校過去問
この動画を見る
$x$を$x-n+a$と表す.
$ x^2+a^2=8$のとき,$n=\Box,x=\Box$である.
灘高校過去問
みんながミスする問題

【「分かる」と「知ってる」は違う…!】文字式:立命館高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
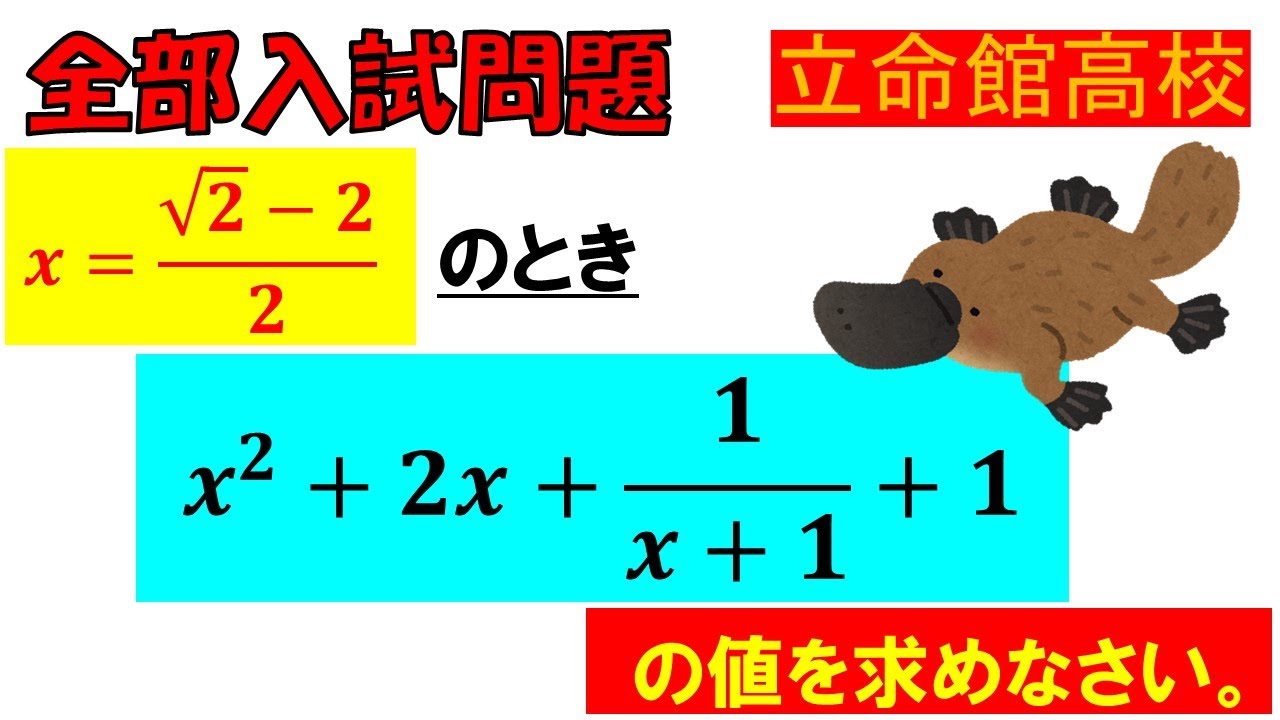
$ x=\dfrac{\sqrt2-2}{2}$のとき,$x^2+2x+\dfrac{1}{x+1}+1$の値を求めなさい.
立命館高校過去問
この動画を見る
$ x=\dfrac{\sqrt2-2}{2}$のとき,$x^2+2x+\dfrac{1}{x+1}+1$の値を求めなさい.
立命館高校過去問
【いかに論理的に説明するか…!】整数:法政大学高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#整数の性質#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$n$を8で割ったときの余り$r$について$n=7r$が成り立つ.
$n$の値を求めなさい.
法政大高校過去問
この動画を見る
$n$を8で割ったときの余り$r$について$n=7r$が成り立つ.
$n$の値を求めなさい.
法政大高校過去問
【真実はいつも一つなんだろうけれど…】文字式:西大和学園高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\dfrac{1}{a}+\dfrac{2}{b}=\dfrac{1}{ca}$
$a$について解け.
西大和学園高等学校過去問
この動画を見る
$\dfrac{1}{a}+\dfrac{2}{b}=\dfrac{1}{ca}$
$a$について解け.
西大和学園高等学校過去問
【中学数学】中学数学:数学検定3級2次:問題1・2

単元:
#数学(中学生)#中1数学#中2数学#式の計算(単項式・多項式・式の四則計算)#数学検定・数学甲子園・数学オリンピック等#空間図形#文字と式#数学検定#数学検定3級
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題1.右の図は、縦の長さがa ㎝、横の長さがb ㎝の長方形と、1辺の長さがc ㎝の正方形です。次の問いに答えなさい。
(1) 長方形の周の長さを、a、b を用いて表しなさい。
(2) 長方形の面積の2倍と正方形の面積を合わせた面積は150 ㎝²未満です。この数量の関係を表した式はどれですか。
下の①~⑥の中から1つ選びなさい。
① 2ab + c² > 150 ② 2ab + c² ≧ 150 ③ 2ab + c² < 150
④ 2ab + c² ≦ 150 ⑤ a²b²+ c² < 150 ⑥ a²b²+ c² ≦ 150
問題2.底面が1辺8㎝の正方形で、高さが6㎝の2つの正四角錐があります。右の図の八面体ABCDEFは、この2つの正四角錐を
ぴったり合わせたものです。次の問いに答えなさい。
(3) 辺CDとねじれの位置にある辺はどれですか。すべて答えなさい。
(4) この八面体の体積は何㎝³ですか。単位をつけて答えなさい。
この動画を見る
問題1.右の図は、縦の長さがa ㎝、横の長さがb ㎝の長方形と、1辺の長さがc ㎝の正方形です。次の問いに答えなさい。
(1) 長方形の周の長さを、a、b を用いて表しなさい。
(2) 長方形の面積の2倍と正方形の面積を合わせた面積は150 ㎝²未満です。この数量の関係を表した式はどれですか。
下の①~⑥の中から1つ選びなさい。
① 2ab + c² > 150 ② 2ab + c² ≧ 150 ③ 2ab + c² < 150
④ 2ab + c² ≦ 150 ⑤ a²b²+ c² < 150 ⑥ a²b²+ c² ≦ 150
問題2.底面が1辺8㎝の正方形で、高さが6㎝の2つの正四角錐があります。右の図の八面体ABCDEFは、この2つの正四角錐を
ぴったり合わせたものです。次の問いに答えなさい。
(3) 辺CDとねじれの位置にある辺はどれですか。すべて答えなさい。
(4) この八面体の体積は何㎝³ですか。単位をつけて答えなさい。
【知ってる手法で地道に攻めようか】文字式:静岡県公立高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$a=\dfrac{2}{7}$のとき,
$(a-5)(a-6)-a(a+3)$の値を求めなさい.
静岡県高校過去問
この動画を見る
$a=\dfrac{2}{7}$のとき,
$(a-5)(a-6)-a(a+3)$の値を求めなさい.
静岡県高校過去問
【中学数学】文字のかけ算・割り算~計算のテクニック~ 2-4【中1数学】

単元:
#数学(中学生)#中1数学#文字と式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
次の式を計算しなさい。
(1) $3 \times 2y$ (2) $(2x+1) \times (-2)$ (3) $2(3x+1) + 3(x+y)$
(4) $(2x+8) \div (-2)$ (5) $(7x^2+3x+1) \div 2x$ (6) $\frac{x+1}{5} \times 10$
(7) $(5s-2) - 3(s-1) + 7$
この動画を見る
次の式を計算しなさい。
(1) $3 \times 2y$ (2) $(2x+1) \times (-2)$ (3) $2(3x+1) + 3(x+y)$
(4) $(2x+8) \div (-2)$ (5) $(7x^2+3x+1) \div 2x$ (6) $\frac{x+1}{5} \times 10$
(7) $(5s-2) - 3(s-1) + 7$
【中学数学】文字式の利用の宿題Live【中1夏期講習③】

単元:
#数学(中学生)#中1数学#文字と式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
問1. 次の文章を文字を使って表せ。
(1)時速5 kmで、x時間歩いた時の道のり
(2)道のりx kmのランニングコースを2時間かかって走ったときの速さ
(3)百の位の数をx、十の位の数をy、一の位の数をzとしたときの、3桁の自然数
(4)1回目の点数がa点、2回目の点数がb点、3回目の点数がc点である3回のテストの平均点
問2. 次の数量の関係を等式で表せ
(1)a才の兄はb才の弟より6才年上である
(2)1個8 kgの荷物がx個あるときの重さはy kgである
(3)1個a円のケーキを2つ、100円の箱に入れて買ったときの代金の合計はb円だった
(4)40個のアメをx人に2個ずつ分けたら、余りがy個になった
(5)30 kmの道のりを時速x kmで5時間進むとき、残りの道のりはy kmである
この動画を見る
問1. 次の文章を文字を使って表せ。
(1)時速5 kmで、x時間歩いた時の道のり
(2)道のりx kmのランニングコースを2時間かかって走ったときの速さ
(3)百の位の数をx、十の位の数をy、一の位の数をzとしたときの、3桁の自然数
(4)1回目の点数がa点、2回目の点数がb点、3回目の点数がc点である3回のテストの平均点
問2. 次の数量の関係を等式で表せ
(1)a才の兄はb才の弟より6才年上である
(2)1個8 kgの荷物がx個あるときの重さはy kgである
(3)1個a円のケーキを2つ、100円の箱に入れて買ったときの代金の合計はb円だった
(4)40個のアメをx人に2個ずつ分けたら、余りがy個になった
(5)30 kmの道のりを時速x kmで5時間進むとき、残りの道のりはy kmである
【中学数学】文字式の利用~文章題を完璧に~【中1夏期講習③】

単元:
#数学(中学生)#中1数学#文字と式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
問1. 次の文章を文字を使って表せ。
(1)ある公園の面積が$a\,\rm{km^2}$である。このとき、その15%の面積が花壇である。花壇の面積
(2)$x$円の品物を3割引きで買ったときの代金
(3)1辺が$x\,\rm{cm}$の正三角形の周の長さ
(4)十の位の数を$x$、一の位の数を$y$としたときの、2桁の自然数
問2. 次の数量の関係を等式で表せ
(1)$x\,\rm{m}$のリボンを4人で等しく切り分けたとき、1人分のリボンは$y\,\rm{m}$だった
(2)ある数$a$を4倍してから1を引いた数は、$a$に8を足した数に等しい
(3)$500\,\rm{m}$の道のりを分速$x$ mで歩くと、$y$分かかった
(4)定価$a$円の品物の20%引きの値段は$b$円だった
この動画を見る
問1. 次の文章を文字を使って表せ。
(1)ある公園の面積が$a\,\rm{km^2}$である。このとき、その15%の面積が花壇である。花壇の面積
(2)$x$円の品物を3割引きで買ったときの代金
(3)1辺が$x\,\rm{cm}$の正三角形の周の長さ
(4)十の位の数を$x$、一の位の数を$y$としたときの、2桁の自然数
問2. 次の数量の関係を等式で表せ
(1)$x\,\rm{m}$のリボンを4人で等しく切り分けたとき、1人分のリボンは$y\,\rm{m}$だった
(2)ある数$a$を4倍してから1を引いた数は、$a$に8を足した数に等しい
(3)$500\,\rm{m}$の道のりを分速$x$ mで歩くと、$y$分かかった
(4)定価$a$円の品物の20%引きの値段は$b$円だった
【中学数学】文字式の計算の宿題Live【中1夏期講習②】

単元:
#数学(中学生)#中1数学#文字と式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
(1) $8(\displaystyle \frac{3}{4}x+\displaystyle \frac{5}{2}y)$
(2) $12(\displaystyle \frac{3x+2}{2}-\displaystyle \frac{2x-1}{3})$
(3) $\displaystyle \frac{3x+2}{6}\times(-12)$
(4) $\displaystyle \frac{3x+2}{3}-\displaystyle \frac{2x-1}{2}$
(5) $\displaystyle \frac{3x-2}{3}-\displaystyle \frac{2x+3}{4}$
(6) $\displaystyle \frac{3(x-1)}{3}+\displaystyle \frac{2(x+2)}{3}$
(7) $\displaystyle 2(3x+4)+4(2x+6)$
(8) $\displaystyle 4(5x-2y)+3(6x+7y)$
(9) $\displaystyle 2(-3a+5b)-6(a-2b)$
(10) $\displaystyle 6(2x-3y)-4(x-5y)$
この動画を見る
(1) $8(\displaystyle \frac{3}{4}x+\displaystyle \frac{5}{2}y)$
(2) $12(\displaystyle \frac{3x+2}{2}-\displaystyle \frac{2x-1}{3})$
(3) $\displaystyle \frac{3x+2}{6}\times(-12)$
(4) $\displaystyle \frac{3x+2}{3}-\displaystyle \frac{2x-1}{2}$
(5) $\displaystyle \frac{3x-2}{3}-\displaystyle \frac{2x+3}{4}$
(6) $\displaystyle \frac{3(x-1)}{3}+\displaystyle \frac{2(x+2)}{3}$
(7) $\displaystyle 2(3x+4)+4(2x+6)$
(8) $\displaystyle 4(5x-2y)+3(6x+7y)$
(9) $\displaystyle 2(-3a+5b)-6(a-2b)$
(10) $\displaystyle 6(2x-3y)-4(x-5y)$
【ルールを再確認する3分間!】文字式:近畿大学附属高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\dfrac{5x+12y}{9}-\dfrac{3x-7y}{6}$を計算せよ.
近大付属高校過去問
この動画を見る
$\dfrac{5x+12y}{9}-\dfrac{3x-7y}{6}$を計算せよ.
近大付属高校過去問
【中学数学】文字式の計算の総復習【中1夏期講習②】

単元:
#数学(中学生)#中1数学#文字と式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$(1)2(3x+1)+4(x-6)$
$(2)\displaystyle \frac{1}{2}(3x-6)-\frac{2}{3}(x-6)$
$(3)\displaystyle 4(x+\frac{1}{2})+6(x-\frac{2}{3})$
$(4)2(x+1)-3(x-5)$
$(5)\displaystyle15(\frac{x+1}{3}+\frac{x-2}{5})$
$(6)\displaystyle12(\frac{3x+2}{2}-\frac{2x-1}{3})$
$(7)\displaystyle \frac{x+3}{4}\times 12$
$(8)\displaystyle \frac{5x-8}{2}\times (-6)$
この動画を見る
$(1)2(3x+1)+4(x-6)$
$(2)\displaystyle \frac{1}{2}(3x-6)-\frac{2}{3}(x-6)$
$(3)\displaystyle 4(x+\frac{1}{2})+6(x-\frac{2}{3})$
$(4)2(x+1)-3(x-5)$
$(5)\displaystyle15(\frac{x+1}{3}+\frac{x-2}{5})$
$(6)\displaystyle12(\frac{3x+2}{2}-\frac{2x-1}{3})$
$(7)\displaystyle \frac{x+3}{4}\times 12$
$(8)\displaystyle \frac{5x-8}{2}\times (-6)$
