 文字と式
文字と式
 文字と式
文字と式
【割合難問】中3冬特訓(特別編)

単元:
#数学(中学生)#中3数学#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①
ある商品をいくつか仕入れた。
この商品を定価の25%引きで売ったとき、仕入れた個数の 5%が売れ残っても、仕入れ総額の14%以上の利益が出るようにしたい。定価を仕入れ値の何%増し以上にすればよいか答えなさい。
この動画を見る
①
ある商品をいくつか仕入れた。
この商品を定価の25%引きで売ったとき、仕入れた個数の 5%が売れ残っても、仕入れ総額の14%以上の利益が出るようにしたい。定価を仕入れ値の何%増し以上にすればよいか答えなさい。
【高校受験対策】数学-死守35

単元:
#数学(中学生)#中1数学#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#平方根#1次関数#平行と合同#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守35
①$6a \div -(\frac{3}{2})$
➁$9-(-15)\div3$
③$\sqrt{54}+4\sqrt{6}$
④$4x^2 \times -\frac{5}{6}xy$
⑤$\sqrt{18}-\frac{4}{\sqrt{2}}$
⑥
$2x+5y=3$
$x-3y=7$
⑦$x=19$のとき、$x^2-10x+9$の値を求めなさい。
⑧2次方程式$x^2+3x-0$を解きなさい
⑨直線$y=-x+7$に平行で、点$(4,-1)$を通る直線の式を求めなさい。
⑩右の図のような五角柱ABCDEFGHIJにおいて、 辺AFとねじれの位置にある辺の数を求めなさい。
⑪半径が$6cm$、中心角が$40°$のおうぎ形の面積を求めなさい。 ただし円周率は$\pi$とする。
⑫$8\leqq \sqrt{n} \leqq9$にあてはまる自然数$n$は、全部で何個あるか求めなさい。
⑬
袋の中に赤玉が3個、白玉が2個入っています。
この袋の中から2個の玉を同時に取り出すとき、取り出した2個の玉が同じ色である確率を求めなさい。ただし、どの玉の取り出し方も同様に確からしいものとします。
⑭
底面の半径が$4cm$で、表面積が$84\pi cm^2$の円柱がある。
この円柱の体積を求めなさい。ただし円周率は$\pi$とする。
この動画を見る
高校受験対策・死守35
①$6a \div -(\frac{3}{2})$
➁$9-(-15)\div3$
③$\sqrt{54}+4\sqrt{6}$
④$4x^2 \times -\frac{5}{6}xy$
⑤$\sqrt{18}-\frac{4}{\sqrt{2}}$
⑥
$2x+5y=3$
$x-3y=7$
⑦$x=19$のとき、$x^2-10x+9$の値を求めなさい。
⑧2次方程式$x^2+3x-0$を解きなさい
⑨直線$y=-x+7$に平行で、点$(4,-1)$を通る直線の式を求めなさい。
⑩右の図のような五角柱ABCDEFGHIJにおいて、 辺AFとねじれの位置にある辺の数を求めなさい。
⑪半径が$6cm$、中心角が$40°$のおうぎ形の面積を求めなさい。 ただし円周率は$\pi$とする。
⑫$8\leqq \sqrt{n} \leqq9$にあてはまる自然数$n$は、全部で何個あるか求めなさい。
⑬
袋の中に赤玉が3個、白玉が2個入っています。
この袋の中から2個の玉を同時に取り出すとき、取り出した2個の玉が同じ色である確率を求めなさい。ただし、どの玉の取り出し方も同様に確からしいものとします。
⑭
底面の半径が$4cm$で、表面積が$84\pi cm^2$の円柱がある。
この円柱の体積を求めなさい。ただし円周率は$\pi$とする。
福田の一夜漬け数学〜相加平均・相乗平均の関係〜その証明の考察4(受験編)

単元:
#中1数学#方程式#数Ⅱ#数と式#式と証明#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#一次不等式(不等式・絶対値のある方程式・不等式)#恒等式・等式・不等式の証明#文字と式
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}\ n$個の変数の相加・相乗平均の関係を証明せよ。
つまり、$n$個の正の数$\ a_1,a_2,\cdots,a_n$に対して
$\displaystyle \frac{a_1+a_2+\cdots+a_n}{n}$$ \geqq \sqrt[n]{a_1a_2\cdots a_n}$
この動画を見る
${\Large\boxed{1}}\ n$個の変数の相加・相乗平均の関係を証明せよ。
つまり、$n$個の正の数$\ a_1,a_2,\cdots,a_n$に対して
$\displaystyle \frac{a_1+a_2+\cdots+a_n}{n}$$ \geqq \sqrt[n]{a_1a_2\cdots a_n}$
福田の一夜漬け数学〜相加平均・相乗平均の関係〜その証明の考察3(受験編)

単元:
#中1数学#中2数学#中3数学#方程式#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根#数と式#式と証明#式の計算(整式・展開・因数分解)#一次不等式(不等式・絶対値のある方程式・不等式)#恒等式・等式・不等式の証明#文字と式
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ $\displaystyle \frac{a+b+c+d}{4} \geqq \sqrt[4]{abcd}$ を既知として、$\displaystyle \frac{a+b+c}{3} \geqq \sqrt[3]{abc}$ を証明せよ。
ただし、$a,b,c,d$は全て正の数であるとする。
${\Large\boxed{2}}\ \boxed{1}$を利用して、$n$個の変数の相加・相乗平均の関係を証明せよ。
つまり、$n$個の正の数$a_1,a_2,\cdot,a_n$に対して
$\displaystyle \frac{a_1+a_2+\cdots+a_n}{n} $$\geqq \sqrt[n]{a_1a_2\cdots a_n}$
この動画を見る
${\Large\boxed{1}}$ $\displaystyle \frac{a+b+c+d}{4} \geqq \sqrt[4]{abcd}$ を既知として、$\displaystyle \frac{a+b+c}{3} \geqq \sqrt[3]{abc}$ を証明せよ。
ただし、$a,b,c,d$は全て正の数であるとする。
${\Large\boxed{2}}\ \boxed{1}$を利用して、$n$個の変数の相加・相乗平均の関係を証明せよ。
つまり、$n$個の正の数$a_1,a_2,\cdot,a_n$に対して
$\displaystyle \frac{a_1+a_2+\cdots+a_n}{n} $$\geqq \sqrt[n]{a_1a_2\cdots a_n}$
【中1 数学】中1-51 反比例の式① ~基本編~

単元:
#数学(中学生)#中1数学#比例・反比例#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
反比例の式といえば①____。
この式で表されるとき、「②__は③__に④____する」という。
またこのときのaを⑤____という。
◎xとyの関係を式に表そう。
⑥yはxに反比例し、x=3のときy=15。
⑦yはxに反比例し、x=-2のときy=6。
⑧yはxに反比例し、x=8のときy=$-\displaystyle \frac{3}{4}$。
⑨yはxに反比例し、x=12のときy=$\displaystyle \frac{4}{3}$である。
x=8のときyの値は?
この動画を見る
反比例の式といえば①____。
この式で表されるとき、「②__は③__に④____する」という。
またこのときのaを⑤____という。
◎xとyの関係を式に表そう。
⑥yはxに反比例し、x=3のときy=15。
⑦yはxに反比例し、x=-2のときy=6。
⑧yはxに反比例し、x=8のときy=$-\displaystyle \frac{3}{4}$。
⑨yはxに反比例し、x=12のときy=$\displaystyle \frac{4}{3}$である。
x=8のときyの値は?
【中1 数学】中1-24 関係を表す式②

単元:
#数学(中学生)#中1数学#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
$2x+5y \lt 3000$のような式を①____っていうよ。
ちなみに、 ②____と③____のときは、$\leqq,\geqq$を使って、
④____も含むって意味なんだ!
⑤ある数$X$から$6$をひくと、$5$より小さい。
⑥ある数$a$の$4$倍からろをひいた数は、 もとの数$a$の$2$倍より大きい。
⑦$1$個$X$円のりんご$3$個と、$1$個$8$円の メロン$1$個を買うと、$1200$円以下だった。
⑧$X$と$y$の積は$12$未満である。
⑨$30m$のテープから、$Xm$のテープを$5$本
切り取ると、$ym$以上のテープが残る。
⑩$3$人で$a$円ずつ出すと、$5000$円のものを
買うことができる。
この動画を見る
$2x+5y \lt 3000$のような式を①____っていうよ。
ちなみに、 ②____と③____のときは、$\leqq,\geqq$を使って、
④____も含むって意味なんだ!
⑤ある数$X$から$6$をひくと、$5$より小さい。
⑥ある数$a$の$4$倍からろをひいた数は、 もとの数$a$の$2$倍より大きい。
⑦$1$個$X$円のりんご$3$個と、$1$個$8$円の メロン$1$個を買うと、$1200$円以下だった。
⑧$X$と$y$の積は$12$未満である。
⑨$30m$のテープから、$Xm$のテープを$5$本
切り取ると、$ym$以上のテープが残る。
⑩$3$人で$a$円ずつ出すと、$5000$円のものを
買うことができる。
【中1 数学】中1-23 関係を表す式①

単元:
#数学(中学生)#中1数学#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
$3x+2y=2000$のような式を①___といって、$=$の左側を②___、
右側を、③___あわせて④___っていうよ!!
◎上のような式をつくろう!!
⑤$1$個$X$円のおかしを$4$個買うと
代金は$y$円です。
⑥$5000$円で$1$着の$a$円の服を$3$着買うと
おつりが$560$円です。
⑦$X$個のあめを、$y$人に$1$人$5$個ずつ
配ると$3$個余る。
⑧$a$枚の紙を、$7$枚ずつ$b$人に配ると
$5$枚足りない。
⑨$1$個$×$円のケーキ$3$個と、$1$個$y$円
のシュークリーム$5$個買うと$1850$円だった。
この動画を見る
$3x+2y=2000$のような式を①___といって、$=$の左側を②___、
右側を、③___あわせて④___っていうよ!!
◎上のような式をつくろう!!
⑤$1$個$X$円のおかしを$4$個買うと
代金は$y$円です。
⑥$5000$円で$1$着の$a$円の服を$3$着買うと
おつりが$560$円です。
⑦$X$個のあめを、$y$人に$1$人$5$個ずつ
配ると$3$個余る。
⑧$a$枚の紙を、$7$枚ずつ$b$人に配ると
$5$枚足りない。
⑨$1$個$×$円のケーキ$3$個と、$1$個$y$円
のシュークリーム$5$個買うと$1850$円だった。
【中1 数学】中1-25 関係を表す式③

単元:
#数学(中学生)#中1数学#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎あるテーマパークの入場料は、
おとな$1$人が$x$円、子ども$1$人が$y$円です。
このとき、次の式はどんなことを表しているかな?
◎$2x+3y=21100$
おとな①___人分と子ども②___人分の 入場料が③______ 。
◎$x - y = 1300$
④___と___⑤の⑥___が$1300$円である。
◎$x + 2y \gt 10000$
おとな⑦___人分と子ども⑧___人分の入場料が⑨_________。
◎$x+2y \leqq 15000$
おとな⑩___人分と子ども⑪___人分の入場料が⑫___。
この動画を見る
◎あるテーマパークの入場料は、
おとな$1$人が$x$円、子ども$1$人が$y$円です。
このとき、次の式はどんなことを表しているかな?
◎$2x+3y=21100$
おとな①___人分と子ども②___人分の 入場料が③______ 。
◎$x - y = 1300$
④___と___⑤の⑥___が$1300$円である。
◎$x + 2y \gt 10000$
おとな⑦___人分と子ども⑧___人分の入場料が⑨_________。
◎$x+2y \leqq 15000$
おとな⑩___人分と子ども⑪___人分の入場料が⑫___。
【中1 数学】中1-22 文字式と数の乗法・除法②
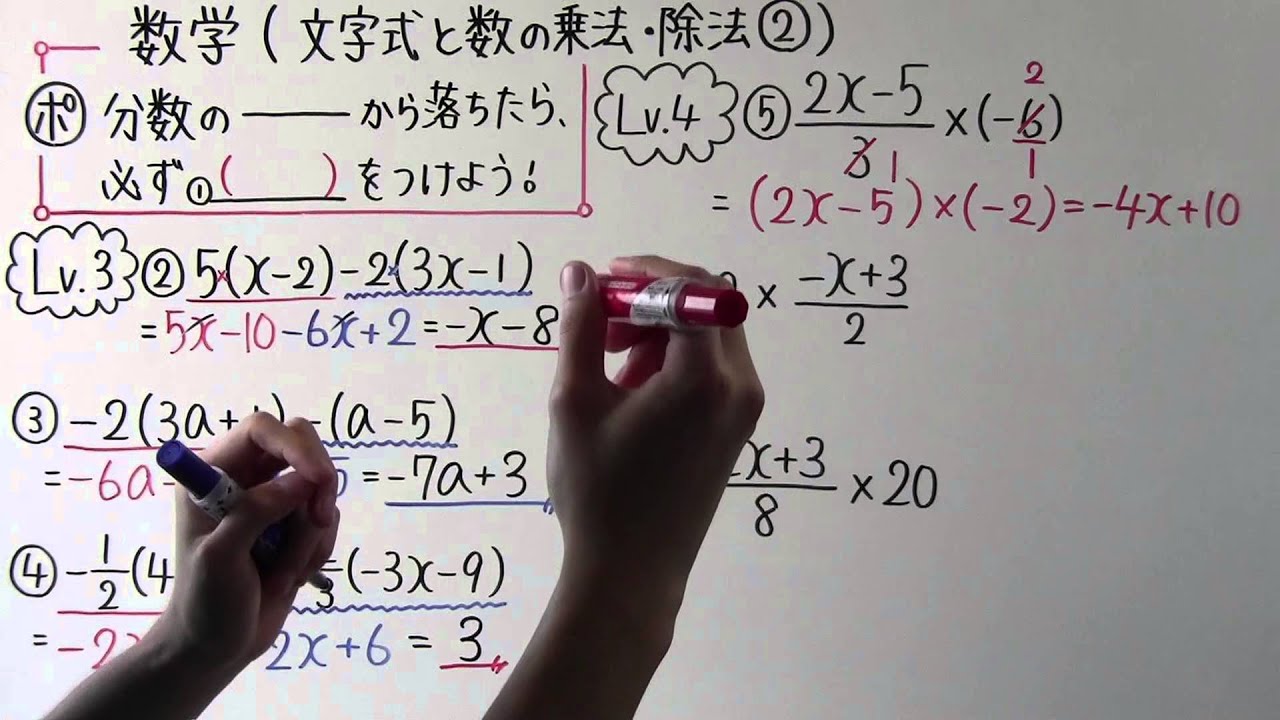
単元:
#数学(中学生)#中1数学#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
分数の___から落ちたら、
必ず①___をつけよう!
【レベル3】
②$5(x-2)-2(3x-1)=$
③$-2(3a+1)-(a-5)=$
④$-\displaystyle \frac{1}{2}(4)(+6)-\displaystyle \frac{2}{3}(-3)(-9)=$
【レベル4】
⑤$\displaystyle \frac{2x-5}{3} \times (-6)=$
⑥$12 \times \displaystyle \frac{-x+3}{2}=$
⑦$\displaystyle \frac{2x+3}{8} \times 20=$
この動画を見る
分数の___から落ちたら、
必ず①___をつけよう!
【レベル3】
②$5(x-2)-2(3x-1)=$
③$-2(3a+1)-(a-5)=$
④$-\displaystyle \frac{1}{2}(4)(+6)-\displaystyle \frac{2}{3}(-3)(-9)=$
【レベル4】
⑤$\displaystyle \frac{2x-5}{3} \times (-6)=$
⑥$12 \times \displaystyle \frac{-x+3}{2}=$
⑦$\displaystyle \frac{2x+3}{8} \times 20=$
【中1 数学】中1-21 文字式と数の乗法・除法①

単元:
#数学(中学生)#中1数学#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
( )に$\times ,\div$がくっついているなら
①____法則を使おう!
【レベル1】
$3x\times(-4)=$
$(-5x)\times(-3)=$
$-18a \div9=$
$4x \times (-\displaystyle \frac{3}{2})=$
$10x \div (-\displaystyle \frac{5}{2})$
【レベル2】
$3(2x-4)=$
$(-y+3)\times (-2)=$
$(12x-9) \div (-6)=$
$-6(\displaystyle \frac{4}{3} x-1)=$
$\displaystyle \frac{3}{2}(6a-2)=$
$(6x-9) \div \displaystyle \frac{3}{4}=$
この動画を見る
( )に$\times ,\div$がくっついているなら
①____法則を使おう!
【レベル1】
$3x\times(-4)=$
$(-5x)\times(-3)=$
$-18a \div9=$
$4x \times (-\displaystyle \frac{3}{2})=$
$10x \div (-\displaystyle \frac{5}{2})$
【レベル2】
$3(2x-4)=$
$(-y+3)\times (-2)=$
$(12x-9) \div (-6)=$
$-6(\displaystyle \frac{4}{3} x-1)=$
$\displaystyle \frac{3}{2}(6a-2)=$
$(6x-9) \div \displaystyle \frac{3}{4}=$
【中1 数学】中1-20 文字式の加法・減法②

単元:
#数学(中学生)#中1数学#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
( )の前に +があれば① ____はずす。
( )の前に - がいるなら② ____はずすんだ!!
③$2x+(5x-4)$
④$-5x-(-7)(+3)$
⑤$2x-9-(x-3)$
⑥$9-(2)(+9)$
◎$5x-3,-7x-5$について…
⑦$2$つの式を足すと?
⑧左の式から右の式を引くと?
この動画を見る
( )の前に +があれば① ____はずす。
( )の前に - がいるなら② ____はずすんだ!!
③$2x+(5x-4)$
④$-5x-(-7)(+3)$
⑤$2x-9-(x-3)$
⑥$9-(2)(+9)$
◎$5x-3,-7x-5$について…
⑦$2$つの式を足すと?
⑧左の式から右の式を引くと?
【中1 数学】中1-19 文字式の加法・減法①
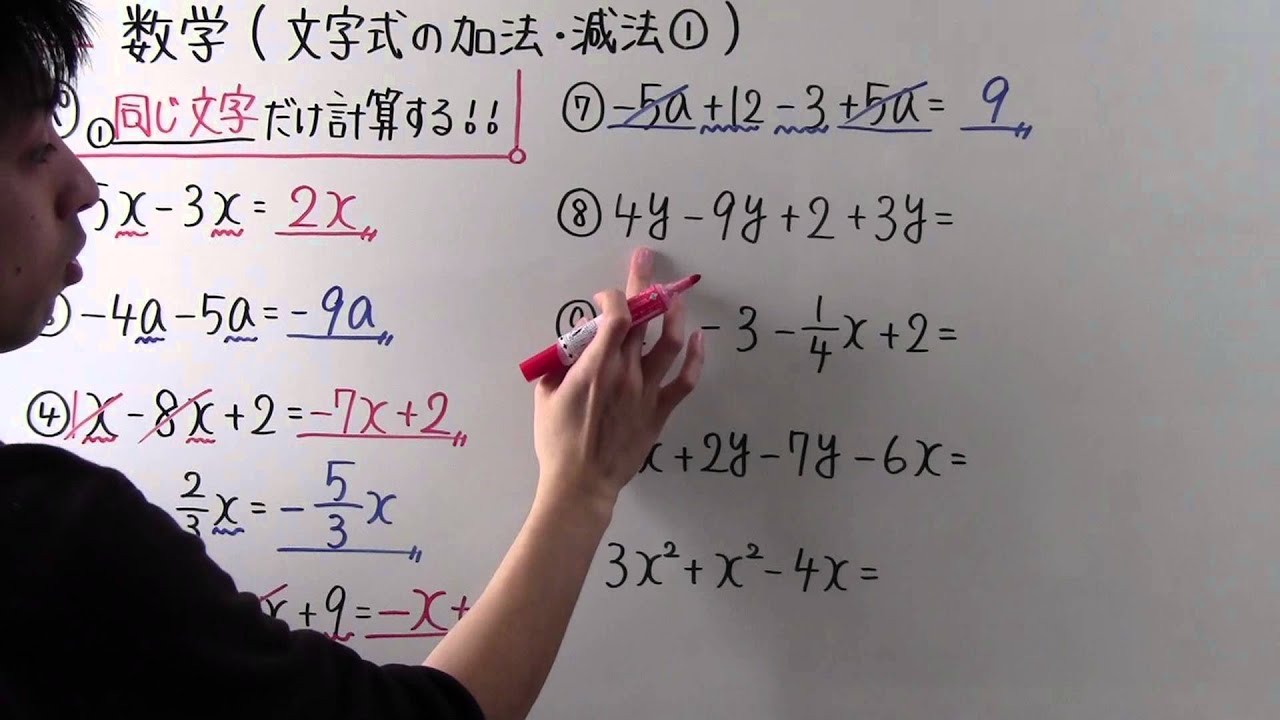
単元:
#数学(中学生)#中1数学#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
① ____だけ計算する!
②$5x-3x=$
③$-4a-5a=$
④$x-8x+2=$
⑤$-x-\displaystyle \frac{2}{3} x=$
⑥$2x-5-3x+9=$
⑦$-5a+12-3+5a=$
⑧$4y-9y+2+3y=$
⑨$2x-3-\displaystyle \frac{1}{4}x+2 =$
⑩$5x+2y-7y-6x=$
⑪$3x^2+x^2-4x=$
この動画を見る
① ____だけ計算する!
②$5x-3x=$
③$-4a-5a=$
④$x-8x+2=$
⑤$-x-\displaystyle \frac{2}{3} x=$
⑥$2x-5-3x+9=$
⑦$-5a+12-3+5a=$
⑧$4y-9y+2+3y=$
⑨$2x-3-\displaystyle \frac{1}{4}x+2 =$
⑩$5x+2y-7y-6x=$
⑪$3x^2+x^2-4x=$
【中1 数学】中1-17 式の値
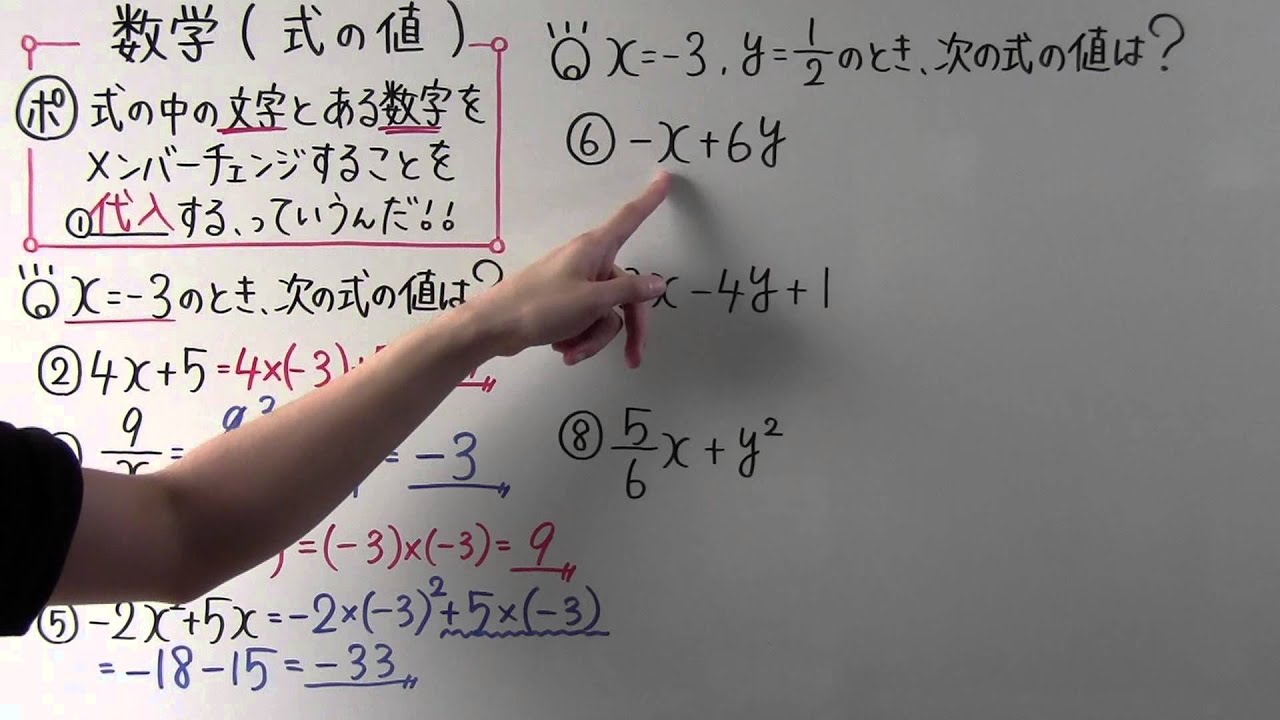
単元:
#数学(中学生)#中1数学#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
式の中の文字とある数字をメンバーチェンジすることを① ____する、っていうんだ!!
◎$x=-3$のとき、次の式の値は?
②$4x+5$
③$\displaystyle \frac{9}{x} $
④$x^2$
⑤$-x^2+5x$
◎$x=-3,y=\displaystyle \frac{1}{2}$のとき、次の値は?
⑥$-x+6y$
⑦$3x-4y+1$
⑧$\displaystyle \frac{5}{6} x +y^2$
この動画を見る
式の中の文字とある数字をメンバーチェンジすることを① ____する、っていうんだ!!
◎$x=-3$のとき、次の式の値は?
②$4x+5$
③$\displaystyle \frac{9}{x} $
④$x^2$
⑤$-x^2+5x$
◎$x=-3,y=\displaystyle \frac{1}{2}$のとき、次の値は?
⑥$-x+6y$
⑦$3x-4y+1$
⑧$\displaystyle \frac{5}{6} x +y^2$
【中1 数学】中1-18 項と係数

単元:
#数学(中学生)#中1数学#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
式の1つ1つの① _____を項といい、答えるときに② _____はつけないでね!
あと、③ _____にくっついている④ _____を係数って言うんだ。
◎項と係数を答えよう!!
⑤ $3x-2y+5$
→項
→係
⑥$-a+ \displaystyle \frac{b}{5} $
→項
→係
㋐$5x$
㋑$3x+4$
㋒$2x^2$
㋓$ \displaystyle \frac{1}{2} +4y+5$
㋔$3xy$
◎㋐〜㋔の中で、一次式は⑦ _____だね!!
この動画を見る
式の1つ1つの① _____を項といい、答えるときに② _____はつけないでね!
あと、③ _____にくっついている④ _____を係数って言うんだ。
◎項と係数を答えよう!!
⑤ $3x-2y+5$
→項
→係
⑥$-a+ \displaystyle \frac{b}{5} $
→項
→係
㋐$5x$
㋑$3x+4$
㋒$2x^2$
㋓$ \displaystyle \frac{1}{2} +4y+5$
㋔$3xy$
◎㋐〜㋔の中で、一次式は⑦ _____だね!!
【中1 数学】中1-15 文字式を作ろう④ ~色々編~

単元:
#数学(中学生)#中1数学#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$1$辺がa㎝の正方形の周の長さは?
②縦の長さが$b㎝$,横の長さが$ C㎝$の長方形の周の長さは?
③周の長さが$ℓ㎝$の長方形で、縦の長さが$a㎝$のとき、横の長さは?
④長さが$x㎝$のテープから、$y㎝$のテープを$5$本切ったときの残りは?
⑤$9$でわると商が$x$であまりが$5$になる数は?
⑥男子$15$人の平均点が$x$点、女子$17$人の平均点が$y$点の時、男女全体の平均点は?
この動画を見る
①$1$辺がa㎝の正方形の周の長さは?
②縦の長さが$b㎝$,横の長さが$ C㎝$の長方形の周の長さは?
③周の長さが$ℓ㎝$の長方形で、縦の長さが$a㎝$のとき、横の長さは?
④長さが$x㎝$のテープから、$y㎝$のテープを$5$本切ったときの残りは?
⑤$9$でわると商が$x$であまりが$5$になる数は?
⑥男子$15$人の平均点が$x$点、女子$17$人の平均点が$y$点の時、男女全体の平均点は?
【中1数学】中1-16 文字式を作ろう⑤ ~式の意味編~

単元:
#数学(中学生)#中1数学#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎それぞれの式は何を表している?
ある映画館では、おとな1人$x $円、こども1人$y$円でチケットが売られている。
→$x+2y$→①____________
→$x-y$→② ____________
縦$a cm$ ,横$b cm$の長方形がある。
→$2a+2b$→③ ____________
→$ab$→④ ____________
縦$a cm$ ,横$b cm$,高さ $C cm$の立方体がある。
→$abc$→⑤ ____________
→$4(a+b+c)$→⑥ ____________
家から公園まで分速$80m$で$x$分間歩き、
公園から駅まで分速$150m$ で$y$分間走って行った。
→$x+y$→⑦ ____________
→$80x+150y$→⑧ ____________
この動画を見る
◎それぞれの式は何を表している?
ある映画館では、おとな1人$x $円、こども1人$y$円でチケットが売られている。
→$x+2y$→①____________
→$x-y$→② ____________
縦$a cm$ ,横$b cm$の長方形がある。
→$2a+2b$→③ ____________
→$ab$→④ ____________
縦$a cm$ ,横$b cm$,高さ $C cm$の立方体がある。
→$abc$→⑤ ____________
→$4(a+b+c)$→⑥ ____________
家から公園まで分速$80m$で$x$分間歩き、
公園から駅まで分速$150m$ で$y$分間走って行った。
→$x+y$→⑦ ____________
→$80x+150y$→⑧ ____________
【中1 数学】中1-14 文字式を作ろう③ ~割合編~

単元:
#数学(中学生)#中1数学#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
・$xm^2$の3%の面積は?
・定価x円の品物を、定価の25%引きで買ったときの代金は?
・定価a円の品物を、定価の3割引きで買ったときの代金は?
・昨年の新入生の数はm人でした。今年は、昨年より7%増えたそうです。今年の新入生の人数は?
この動画を見る
・$xm^2$の3%の面積は?
・定価x円の品物を、定価の25%引きで買ったときの代金は?
・定価a円の品物を、定価の3割引きで買ったときの代金は?
・昨年の新入生の数はm人でした。今年は、昨年より7%増えたそうです。今年の新入生の人数は?
【中1 数学】中1-13 文字式を作ろう② ~みはじ編~

単元:
#数学(中学生)#中1数学#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
・時速5kmでx時間歩いたときの道のりは?
・akm離れた町まで、時速12kmで行ったときにかかった時間は?
・bkmの道のりを、2時間かけて歩いたときの速さは?
・xkm離れたA町とB町の間を、行きは時速3km、帰りは時速4kmで行ったときに往復でかかった時間は?
この動画を見る
・時速5kmでx時間歩いたときの道のりは?
・akm離れた町まで、時速12kmで行ったときにかかった時間は?
・bkmの道のりを、2時間かけて歩いたときの速さは?
・xkm離れたA町とB町の間を、行きは時速3km、帰りは時速4kmで行ったときに往復でかかった時間は?
【中1 数学】中1-12 文字式を作ろう① ~お金編~

単元:
#数学(中学生)#中1数学#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
・1本150円のジュースをx本買ったときの代金は?
・1個80円のおかしをa個買って150円の入れ物に入れてもらったときの代金は?
・1冊x円の本を3冊買って、2000円出したときのおつりは?
・1個130円のりんごx個と、1個70円のみかんy個を買ったときの代金は?
・5人がa円ずつ出して、b円のものを買ったときの代金は?
・1円硬貨x枚と50円硬貨y枚の合計金額は?
この動画を見る
・1本150円のジュースをx本買ったときの代金は?
・1個80円のおかしをa個買って150円の入れ物に入れてもらったときの代金は?
・1冊x円の本を3冊買って、2000円出したときのおつりは?
・1個130円のりんごx個と、1個70円のみかんy個を買ったときの代金は?
・5人がa円ずつ出して、b円のものを買ったときの代金は?
・1円硬貨x枚と50円硬貨y枚の合計金額は?
【中1 数学】中1-11 文字を使うときのルール
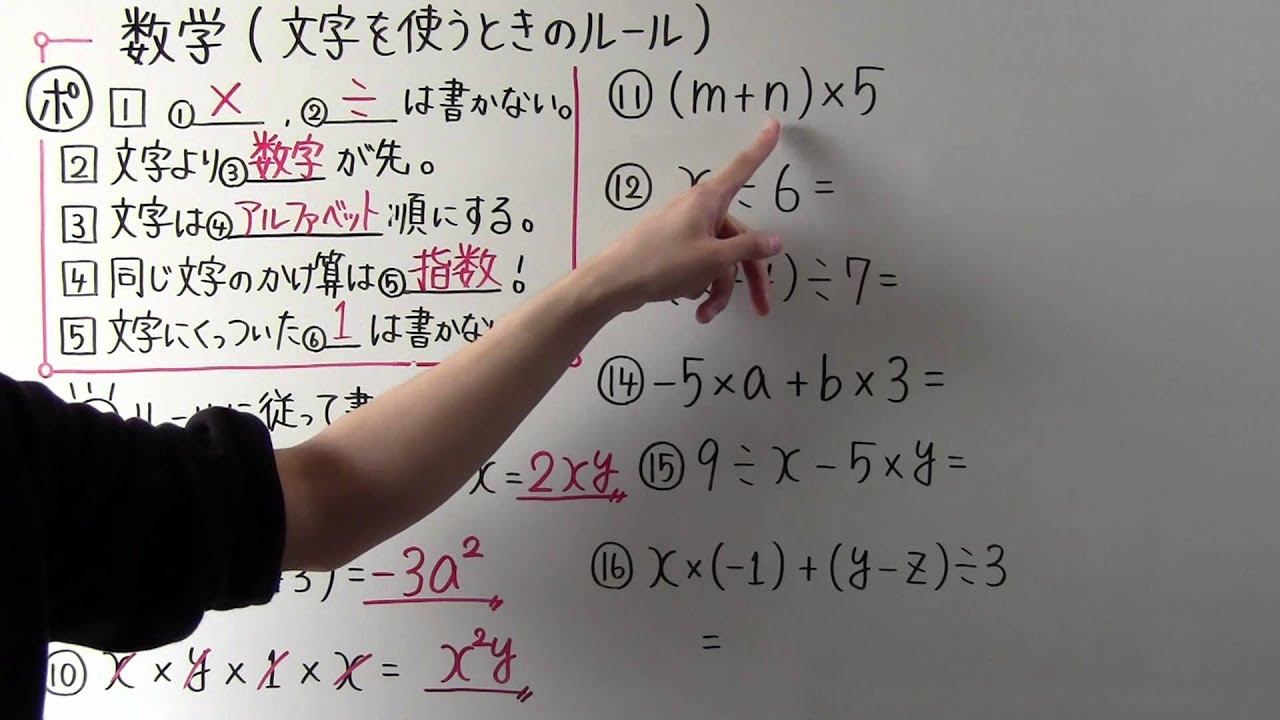
単元:
#数学(中学生)#中1数学#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
$\boxed {1} $ ①,②は書かない
$\boxed {2} $文字より③が先。
$\boxed {3} $文字は④順にする。
$\boxed {4} $同じ文字の掛け算は⑤!
$\boxed {5} $文字にくっついた⑥は書かない
◎ルールに従って書こう!!
⑦$3\times x =$
⑧ $y\times 2 \times x =$
⑨ $a\times a \times (-3) =$
⑩ $x\times y \times 1 \times x=$
⑪ $( m +n) \times 5=$
⑫$x \div 6=$
⑬$(x -y)\div 7=$
⑭$-5\times a + b \times y= $
⑮$9\div x - 5 \times y= $
⑯$x+(-1)+(y-z) \div 3= $
この動画を見る
$\boxed {1} $ ①,②は書かない
$\boxed {2} $文字より③が先。
$\boxed {3} $文字は④順にする。
$\boxed {4} $同じ文字の掛け算は⑤!
$\boxed {5} $文字にくっついた⑥は書かない
◎ルールに従って書こう!!
⑦$3\times x =$
⑧ $y\times 2 \times x =$
⑨ $a\times a \times (-3) =$
⑩ $x\times y \times 1 \times x=$
⑪ $( m +n) \times 5=$
⑫$x \div 6=$
⑬$(x -y)\div 7=$
⑭$-5\times a + b \times y= $
⑮$9\div x - 5 \times y= $
⑯$x+(-1)+(y-z) \div 3= $
【中1 数学】 中1-41 変域

単元:
#数学(中学生)#中1数学#正の数・負の数#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
中1 数学 変域
以下の問に答えよ
・$x$ の変域を不等号を使って表そう!
① $8$ 以上 ⇒
② $7$ より小さい ⇒
③ $-5$ より大きく $6$ 以下 ⇒
④ $-12$ 以上 $3$ 未満 ⇒
⑤ $-7$ より大きく $0$ より小さい ⇒
⑥ $-2$ ~ $5$ ⇒
⑦ $0$ 以上 ⇒
⑧ $-9$ ~ $-3$ ⇒
※図は動画内参照
この動画を見る
中1 数学 変域
以下の問に答えよ
・$x$ の変域を不等号を使って表そう!
① $8$ 以上 ⇒
② $7$ より小さい ⇒
③ $-5$ より大きく $6$ 以下 ⇒
④ $-12$ 以上 $3$ 未満 ⇒
⑤ $-7$ より大きく $0$ より小さい ⇒
⑥ $-2$ ~ $5$ ⇒
⑦ $0$ 以上 ⇒
⑧ $-9$ ~ $-3$ ⇒
※図は動画内参照
【中1 数学】 1-②⑦ ややこしい方程式を解く!
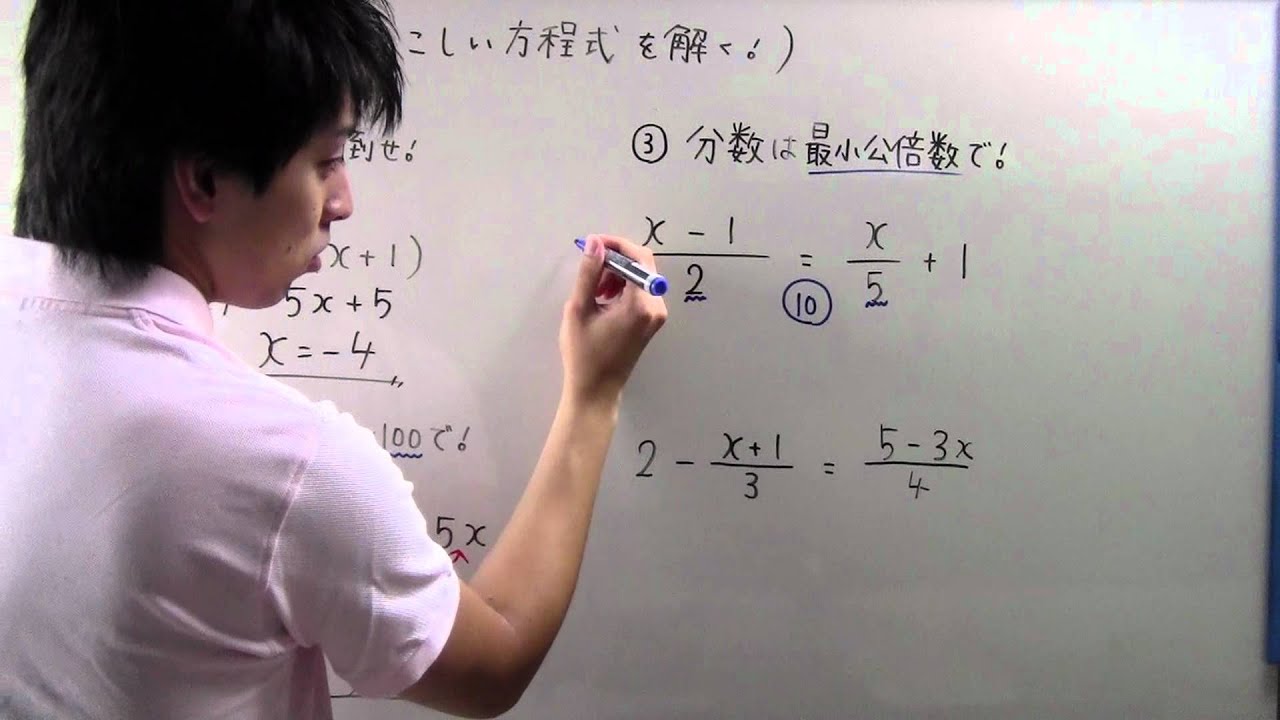
単元:
#数学(中学生)#中1数学#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
中1 数学 ややこしい方程式を解く!
[問題]
次の問に答えよ
①( )は先に倒せ!
- 3(x + 9) = 5(x + 1)
② 小数には、"×10"か"×100"で!
0.2x - 1 = 1.8 - 0.5x
③ 分数は最小公倍数で!
$\frac{(x - 1)}{2} = \frac{x}{5} + 1$
$2 - \frac{(x + 1)}{3} = \frac{(5 - 3x)}{4}$
この動画を見る
中1 数学 ややこしい方程式を解く!
[問題]
次の問に答えよ
①( )は先に倒せ!
- 3(x + 9) = 5(x + 1)
② 小数には、"×10"か"×100"で!
0.2x - 1 = 1.8 - 0.5x
③ 分数は最小公倍数で!
$\frac{(x - 1)}{2} = \frac{x}{5} + 1$
$2 - \frac{(x + 1)}{3} = \frac{(5 - 3x)}{4}$
【中1 数学】 1-②⑥ 方程式を解く!

単元:
#数学(中学生)#中1数学#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
中1 数学 方程式を解く!
[問題]
次の問に答えよ
① x - 3 = 9
② 2 - x = 4
③ 4 x + 6 = - 14
④ 9x - 3 = 5x + 9
⑤ 12 = 3x - 6
この動画を見る
中1 数学 方程式を解く!
[問題]
次の問に答えよ
① x - 3 = 9
② 2 - x = 4
③ 4 x + 6 = - 14
④ 9x - 3 = 5x + 9
⑤ 12 = 3x - 6
【中1 数学】 1-①④ 文章から式に(応用編) 【6~7月】

単元:
#数学(中学生)#中1数学#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
中1 数学 文章から式に(応用編)
① $7$ で割ると、商が $x$ であまりが $3$ になる自然数は?
②男子 $13$ 人の平均が $x$ 、女子 $15$ 人の平均が $y$ のとき、クラス全体の平均は?
③長方形の周の長さが $a$ で、縦の長さが $b$ のとき、横は?
この動画を見る
中1 数学 文章から式に(応用編)
① $7$ で割ると、商が $x$ であまりが $3$ になる自然数は?
②男子 $13$ 人の平均が $x$ 、女子 $15$ 人の平均が $y$ のとき、クラス全体の平均は?
③長方形の周の長さが $a$ で、縦の長さが $b$ のとき、横は?
【中1 数学】 1-①⑧ 文字の計算(乗法・除法)
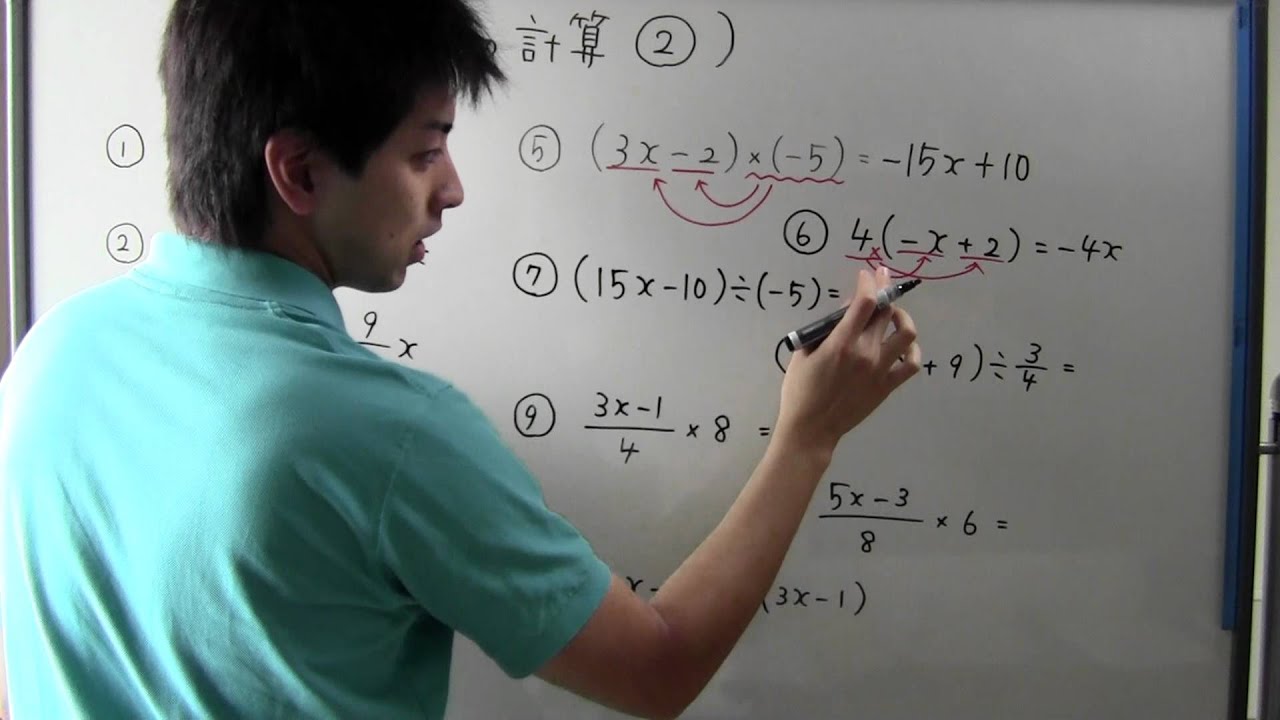
単元:
#数学(中学生)#中1数学#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
中1 数学 文字の計算(乗法・除法)
次の計算をせよ
① $3x \times (-2) =$
② $-15 x \div 5 =$
③ $9x \div 5 =$
④ $12y \div (-\dfrac{3}{4}) =$
⑤ $(3x - 2) \times (- 5) =$
⑥ $4(- x + 2) =$
⑦ $(15x - 10) \div (- 5) =$
⑧ $(27x + 9) \div (\dfrac{3}{4}) =$
⑨ $\dfrac{(3x - 1)}{4} \times 8$
⑩ $\dfrac{(5x - 3)}{8} \times 6 =$
⑪ $5(2x - 3) - 3(3x - 1)=$
この動画を見る
中1 数学 文字の計算(乗法・除法)
次の計算をせよ
① $3x \times (-2) =$
② $-15 x \div 5 =$
③ $9x \div 5 =$
④ $12y \div (-\dfrac{3}{4}) =$
⑤ $(3x - 2) \times (- 5) =$
⑥ $4(- x + 2) =$
⑦ $(15x - 10) \div (- 5) =$
⑧ $(27x + 9) \div (\dfrac{3}{4}) =$
⑨ $\dfrac{(3x - 1)}{4} \times 8$
⑩ $\dfrac{(5x - 3)}{8} \times 6 =$
⑪ $5(2x - 3) - 3(3x - 1)=$
【中1 数学】 1-①⑦ 文字の計算(加法・減法)
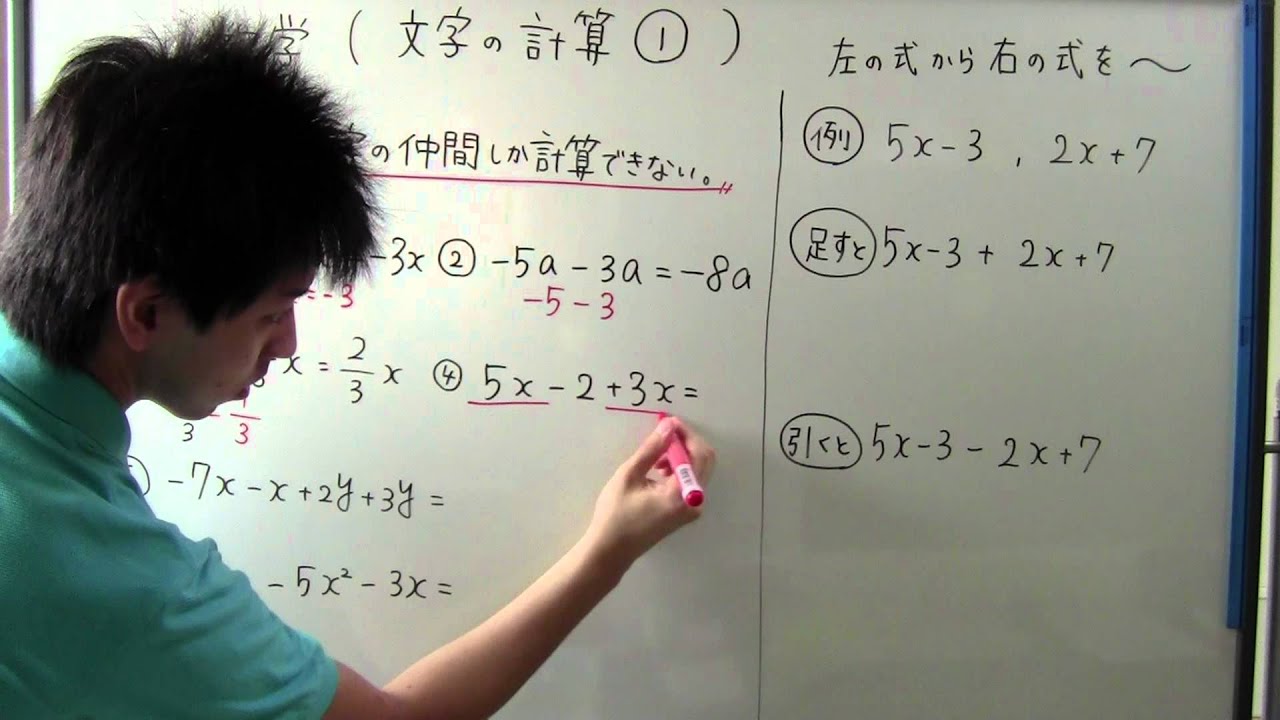
単元:
#数学(中学生)#中1数学#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
中1 数学 文字の計算(加法・減法)
左の式から右の式を~
(例)$5x-3$ 、 $2x+7$
足すと…
$5x-3+2x+7$
引くと…
$5x-3-(2x+7)$
次の計算をせよ
① $-5x+2x=$
② $-5a-3a=$
③ $x-\dfrac{1}{3}x=$
④ $5x-2+3x=$
⑤ $-7x-x+2y+3y=$
⑥ $+9x-5x^2-3x=$
この動画を見る
中1 数学 文字の計算(加法・減法)
左の式から右の式を~
(例)$5x-3$ 、 $2x+7$
足すと…
$5x-3+2x+7$
引くと…
$5x-3-(2x+7)$
次の計算をせよ
① $-5x+2x=$
② $-5a-3a=$
③ $x-\dfrac{1}{3}x=$
④ $5x-2+3x=$
⑤ $-7x-x+2y+3y=$
⑥ $+9x-5x^2-3x=$
【中1 数学】 1-①⑥ 項と係数 【6~7月】
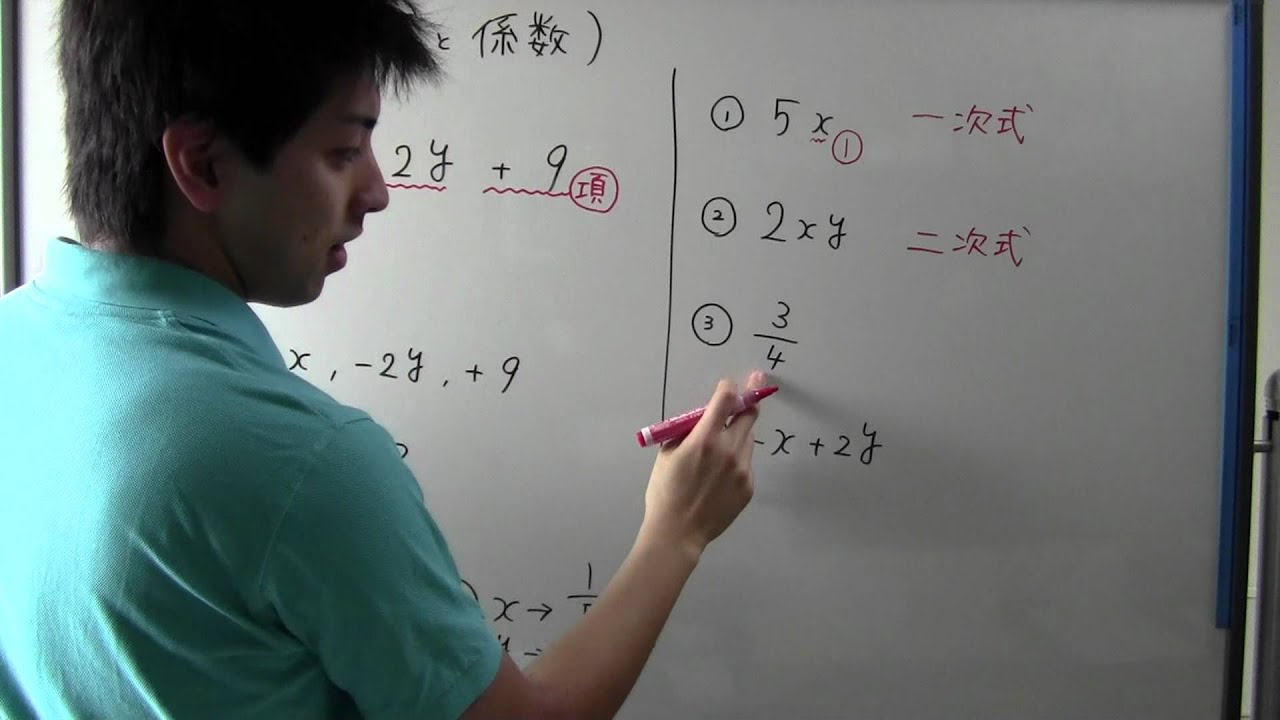
単元:
#数学(中学生)#中1数学#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
中1 数学 項と係数
次の式の項と係数は?
(例)$3x-2y+9$
① $5x$
② $2xy$
③ $\dfrac{3}{4}$
④ $-x+2y$
この動画を見る
中1 数学 項と係数
次の式の項と係数は?
(例)$3x-2y+9$
① $5x$
② $2xy$
③ $\dfrac{3}{4}$
④ $-x+2y$
【中1 数学】 1-①⑤ 代入とは? 【6~7月】
単元:
#数学(中学生)#中1数学#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
中1 数学 代入とは?
以下の問に答えよ
$x=-2$ のとき
① $5-x$ の値は?
② $3x+4$ の値は?
③ $\dfrac{14}{x}$ は?
④ $-x^2$ は?
$x=3$ 、$ y=-4$ のとき
⑤ $-x+\dfrac{1}{2}y$
この動画を見る
中1 数学 代入とは?
以下の問に答えよ
$x=-2$ のとき
① $5-x$ の値は?
② $3x+4$ の値は?
③ $\dfrac{14}{x}$ は?
④ $-x^2$ は?
$x=3$ 、$ y=-4$ のとき
⑤ $-x+\dfrac{1}{2}y$
【中1 数学】 1-①③ 文章→式(割合編) 【6~7月】

単元:
#数学(中学生)#中1数学#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
中1 数学 文章→式(割合編)
次の問題に答えよ
[%シリーズ]
① $x$ の $51$ %は?
② $a$ 人の中の $29$ %は?
[割シリーズ]
① $x$ の $4$ 割は?
② $a$ 円の $2$ 割引きは?
③ $y$ 人から $3$ %増えたら?
この動画を見る
中1 数学 文章→式(割合編)
次の問題に答えよ
[%シリーズ]
① $x$ の $51$ %は?
② $a$ 人の中の $29$ %は?
[割シリーズ]
① $x$ の $4$ 割は?
② $a$ 円の $2$ 割引きは?
③ $y$ 人から $3$ %増えたら?
【中1 数学】 1-①② 文字→式(みはじ編) 【6~7月】

単元:
#数学(中学生)#中1数学#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
中1 数学 文章→式(みはじ編)
次の問題に答えよ
① 時速$3$kmで$x$時間走ったときの道のり。
② $y$kmはなれた嵐子ちゃんの家まで、時速$50$kmで行ったときにかかった時間。
③ $a$kmはなれた店に、行きは時速$4$km、帰りは時速$3$kmで往復した時にかかった時間。
※図は動画内参照
この動画を見る
中1 数学 文章→式(みはじ編)
次の問題に答えよ
① 時速$3$kmで$x$時間走ったときの道のり。
② $y$kmはなれた嵐子ちゃんの家まで、時速$50$kmで行ったときにかかった時間。
③ $a$kmはなれた店に、行きは時速$4$km、帰りは時速$3$kmで往復した時にかかった時間。
※図は動画内参照
