 平面図形
平面図形
 平面図形
平面図形
【高校受験対策】数学-図形20
単元:
#数学(中学生)#中1数学#中2数学#平面図形#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右の図のように、$BC = 2cm 、 AC = 3cm 、\angle ACB = 60°$の
三角形$ABC$と、$DC =\sqrt3 cm 、\angle BDC = 90°$の直角三角形$BDC$がある。
点$P$が辺$BC$上を動くとき、次の各問いに答えなさい。
①$AP+PD$が最も長くなるとき、$AP+PD$の長さを求めなさい。
②$AP+PD$が最も短くなるとき、$AP+PD$の長さを求めなさい。
③点$P$が辺$BC$の中点であるとき、$AP+PD$の長さを求めなさい。
④$AP+PD=4cm$となるとき、$AP$の長さを求めなさい。
図は動画内参照
この動画を見る
右の図のように、$BC = 2cm 、 AC = 3cm 、\angle ACB = 60°$の
三角形$ABC$と、$DC =\sqrt3 cm 、\angle BDC = 90°$の直角三角形$BDC$がある。
点$P$が辺$BC$上を動くとき、次の各問いに答えなさい。
①$AP+PD$が最も長くなるとき、$AP+PD$の長さを求めなさい。
②$AP+PD$が最も短くなるとき、$AP+PD$の長さを求めなさい。
③点$P$が辺$BC$の中点であるとき、$AP+PD$の長さを求めなさい。
④$AP+PD=4cm$となるとき、$AP$の長さを求めなさい。
図は動画内参照
【高校受験対策】数学-図形18

単元:
#数学(中学生)#中1数学#中2数学#中3数学#円#平面図形#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①右の図1のような$\triangle ABC$があります。
点$D、E$はそれぞれ辺$AB、BC$上の点で、$\angle BDE =\angle ACB$です。
$AD = 2cm 、 DB = 8cm 、 BE = 6cm$のとき、$EC$の長さを求めなさい。
② 右の図2は、正方形$ABCD$と、おうぎ形$BAC$、おうぎ形$CBD$を組み合わせたものです。
点$E$は$\stackrel{\huge\frown}{AC}$と$\stackrel{\huge\frown}{BD}$との交点です。
正方形$ABCD$の1辺の長さが$12cm$のとき、$\stackrel{\huge\frown}{BE}$の長さを求めなさい。 ただし、円周率は$\pi$とします。
③右の図3のような四角形$ABCD$があり、対角線$AC$と対角線$BD$との交点を$E$とする。
線分$BE$上に、2点$B、E$と異なる点$F$をとり、直線$AF$と辺$BC$との交点を$G$とする。
四角形$ABCD$の面積が$50cm²$、$△AGC$の面積が$30cm$、
$BF:FD=3:4、AF:FG=2:1$であるとき、$△ACD$の面積は何$cm^2$か。
図は動画内参照
この動画を見る
①右の図1のような$\triangle ABC$があります。
点$D、E$はそれぞれ辺$AB、BC$上の点で、$\angle BDE =\angle ACB$です。
$AD = 2cm 、 DB = 8cm 、 BE = 6cm$のとき、$EC$の長さを求めなさい。
② 右の図2は、正方形$ABCD$と、おうぎ形$BAC$、おうぎ形$CBD$を組み合わせたものです。
点$E$は$\stackrel{\huge\frown}{AC}$と$\stackrel{\huge\frown}{BD}$との交点です。
正方形$ABCD$の1辺の長さが$12cm$のとき、$\stackrel{\huge\frown}{BE}$の長さを求めなさい。 ただし、円周率は$\pi$とします。
③右の図3のような四角形$ABCD$があり、対角線$AC$と対角線$BD$との交点を$E$とする。
線分$BE$上に、2点$B、E$と異なる点$F$をとり、直線$AF$と辺$BC$との交点を$G$とする。
四角形$ABCD$の面積が$50cm²$、$△AGC$の面積が$30cm$、
$BF:FD=3:4、AF:FG=2:1$であるとき、$△ACD$の面積は何$cm^2$か。
図は動画内参照
【テスト対策 中1】6章-2
単元:
#数学(中学生)#中1数学#空間図形#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
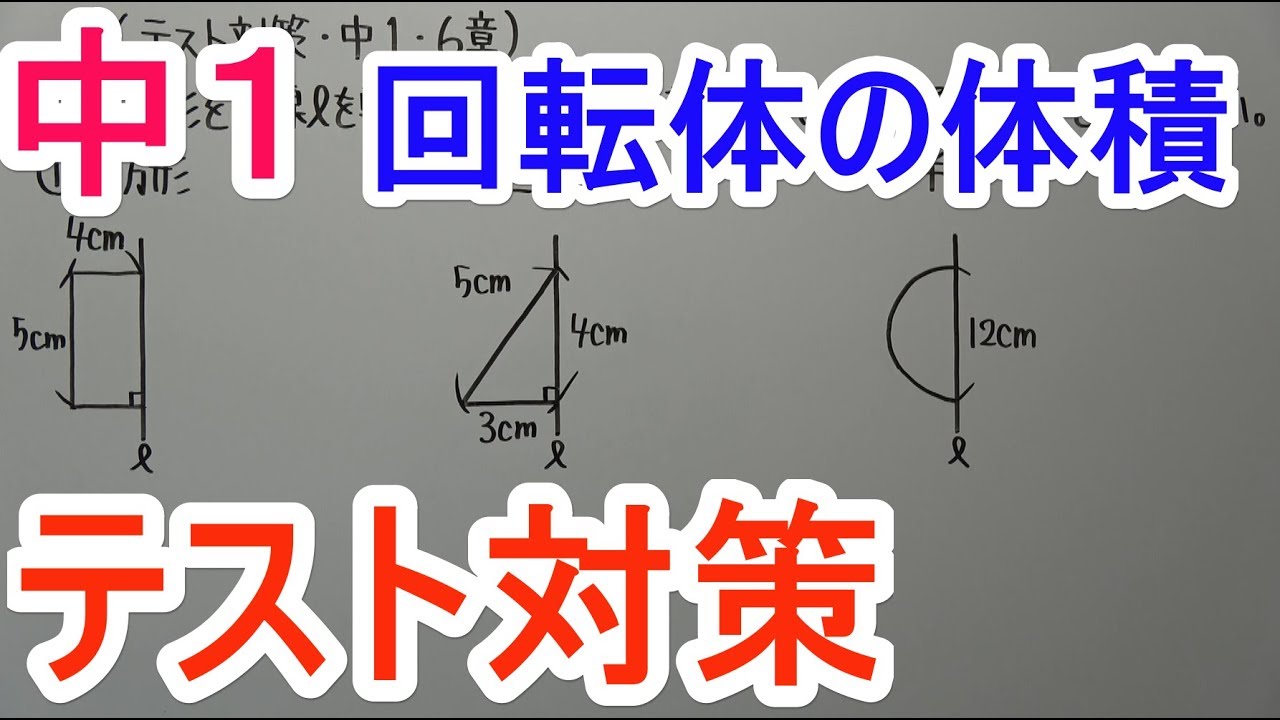
◎次の図形を直線を軸として1回転してできる立体の名前とその体積を求めなさい。
①長方形
②三角形
③半円
図は動画内参照
この動画を見る
◎次の図形を直線を軸として1回転してできる立体の名前とその体積を求めなさい。
①長方形
②三角形
③半円
図は動画内参照
【テスト対策 中1】6章-1

単元:
#数学(中学生)#中1数学#平行と合同#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎次のことがらのうち、つねに成り立つものをすべて選びなさい。
ただし、$\ell、m、n$は直線、$A、B、C$は平面とする。
①$ℓ//m、m\perp n$ならば$\ell \perp n$
②$ℓ//m、m//n$ならば$ℓ//n$
③$\ell \perp m、m\perp n$ならば$\ell //n$
④$ℓ//A、m//A$ならば$ℓ//m$
⑤$\ell \perp A、m\perp A$ならば$ℓ//m$
⑥$A//C、B//C$ならば$A//B$
⑦$A\perp C、B\perp C$ならば$A//B$
⑧$A//B、\ell \perp A$ならば$\ell \perp B$
この動画を見る
◎次のことがらのうち、つねに成り立つものをすべて選びなさい。
ただし、$\ell、m、n$は直線、$A、B、C$は平面とする。
①$ℓ//m、m\perp n$ならば$\ell \perp n$
②$ℓ//m、m//n$ならば$ℓ//n$
③$\ell \perp m、m\perp n$ならば$\ell //n$
④$ℓ//A、m//A$ならば$ℓ//m$
⑤$\ell \perp A、m\perp A$ならば$ℓ//m$
⑥$A//C、B//C$ならば$A//B$
⑦$A\perp C、B\perp C$ならば$A//B$
⑧$A//B、\ell \perp A$ならば$\ell \perp B$
【テスト対策 中1】5章-6

【テスト対策 中1】5章-5

単元:
#数学(中学生)#中1数学#空間図形#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①半径$8cm$、弧の長さ$6\pi cm$のおうぎ形の中心角の大きさと面積を求めなさい。
②中心角72、弧の長さ$4\pi cm$のおうぎ形の半径を求めなさい。
③半径15cmのおうぎ形で、弧の長さが半径6cmの円の周に等しいとき、
このおうぎ形の中心角の大きさを求めなさい。
図は動画内参照
この動画を見る
①半径$8cm$、弧の長さ$6\pi cm$のおうぎ形の中心角の大きさと面積を求めなさい。
②中心角72、弧の長さ$4\pi cm$のおうぎ形の半径を求めなさい。
③半径15cmのおうぎ形で、弧の長さが半径6cmの円の周に等しいとき、
このおうぎ形の中心角の大きさを求めなさい。
図は動画内参照
【テスト対策 中1】5章-2

単元:
#数学(中学生)#中1数学#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎次の$\Box$にあてはまることばを書きなさい。
・平面上で、図形をある点$O$を中心にして一定の角度だけまわすことを$\Box$といい、
点$O$を$\Box$という。
その中で、180℃の$\Box$を$\Box$という。
・平面上で、図形をある直線$\ell$を折り目として折り返すことを$\Box$といい、
直線$\ell$を$\Box$という。
$\Box$で移りあう図形は、$\Box$について$\Box$対で、
対応する点を結んだ線分は$\Box$と$\Box$に交わり、
その交点で$\Box$される。
この動画を見る
◎次の$\Box$にあてはまることばを書きなさい。
・平面上で、図形をある点$O$を中心にして一定の角度だけまわすことを$\Box$といい、
点$O$を$\Box$という。
その中で、180℃の$\Box$を$\Box$という。
・平面上で、図形をある直線$\ell$を折り目として折り返すことを$\Box$といい、
直線$\ell$を$\Box$という。
$\Box$で移りあう図形は、$\Box$について$\Box$対で、
対応する点を結んだ線分は$\Box$と$\Box$に交わり、
その交点で$\Box$される。
【テスト対策 中1】5章-1

単元:
#数学(中学生)#中1数学#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の$\Box$にあてはまることばや記号を書きなさい。
・2直線$AB、CD$が交わってできる角が直角のとき、
$AB$と$CD$は$\Box$であるといい、 ②$AB\Box CD$と表す。
また、2直線$\ell、m$が交わらないとき、$\ell$は$m$はといい、$AB \Box CD$と表す。
・図形の形と大きさを変えないで、位置だけを変えることを$\Box$という。
・平面上で、図形を一定の方向に、一定の長さだけずらすことを$\Box$といい、
このとき、対応する2点を結ぶ線分は、それぞれ$\Box$で長さが$\Box$。
この動画を見る
次の$\Box$にあてはまることばや記号を書きなさい。
・2直線$AB、CD$が交わってできる角が直角のとき、
$AB$と$CD$は$\Box$であるといい、 ②$AB\Box CD$と表す。
また、2直線$\ell、m$が交わらないとき、$\ell$は$m$はといい、$AB \Box CD$と表す。
・図形の形と大きさを変えないで、位置だけを変えることを$\Box$という。
・平面上で、図形を一定の方向に、一定の長さだけずらすことを$\Box$といい、
このとき、対応する2点を結ぶ線分は、それぞれ$\Box$で長さが$\Box$。
【テスト対策 中2】4章-4

単元:
#数学(中学生)#中1数学#角度と面積#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右の図のような図形について、次の各問に答えなさい。
①$\angle a+\angle b+\angle c+\angle d+\angle e$を求めなさい。
② ①を証明しなさい。ただし、解答欄の図に頂点や角度を
書き込んでよいものとする。(例:頂点$F,\angle F$)$
図は動画内参照
この動画を見る
右の図のような図形について、次の各問に答えなさい。
①$\angle a+\angle b+\angle c+\angle d+\angle e$を求めなさい。
② ①を証明しなさい。ただし、解答欄の図に頂点や角度を
書き込んでよいものとする。(例:頂点$F,\angle F$)$
図は動画内参照
【テスト対策 中2】4章-2

単元:
#数学(中学生)#中1数学#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右の図形について$\Box$にあてはまる式や数を書きなさい。
1つの頂点から、ほかの各頂点に対角線を引くと①個の三角形に分けられるので、
内角の和は②で計算できる。
③十二角形の内角の和を求めなさい。
④正九角形の1つの内角の大きさを求めなさい。
⑤正二十角形の1つの外角の大きさを求めなさい。
図は動画内参照
この動画を見る
右の図形について$\Box$にあてはまる式や数を書きなさい。
1つの頂点から、ほかの各頂点に対角線を引くと①個の三角形に分けられるので、
内角の和は②で計算できる。
③十二角形の内角の和を求めなさい。
④正九角形の1つの内角の大きさを求めなさい。
⑤正二十角形の1つの外角の大きさを求めなさい。
図は動画内参照
【高校受験対策】数学-死守8

単元:
#中1数学#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根#文章題#文章題その他#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$4 \times (5+2)$を計算しなさい.
②$\dfrac{2}{3}-\dfrac{1}{5}$を計算しなさい.
③$24\div (-6)$を計算しなさい.
④$3(2x-y)-(x+5y)$を計算しなさい.
⑤連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+3y=8 \\
2x-y=-5
\end{array}
\right.
\end{eqnarray}$を解きなさい.
⑥$x^2+x-56$を因数分解しなさい.
⑦$(\sqrt{27}-\sqrt3)\times \sqrt2$を計算しなさい.
⑧方程式$x^2-5x+1=0$を解きなさい.
⑨下の図のように,$\triangle ABC$の辺$BC$を延長して$CD$とし,
辺$CA$を延長して$AE$とします.
$\angle ABC=41°,\angle ACD=124°$のとき,
$\angle BAE$の大きさは何度ですか.
⑩1箱60円のチョコレートと1個40円のあめが売られています.
このチョコレートとあめを買うとき,代金をちょうど500円にするには,
買い方は全部で何通りありますか.
図は動画内を参照
この動画を見る
①$4 \times (5+2)$を計算しなさい.
②$\dfrac{2}{3}-\dfrac{1}{5}$を計算しなさい.
③$24\div (-6)$を計算しなさい.
④$3(2x-y)-(x+5y)$を計算しなさい.
⑤連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+3y=8 \\
2x-y=-5
\end{array}
\right.
\end{eqnarray}$を解きなさい.
⑥$x^2+x-56$を因数分解しなさい.
⑦$(\sqrt{27}-\sqrt3)\times \sqrt2$を計算しなさい.
⑧方程式$x^2-5x+1=0$を解きなさい.
⑨下の図のように,$\triangle ABC$の辺$BC$を延長して$CD$とし,
辺$CA$を延長して$AE$とします.
$\angle ABC=41°,\angle ACD=124°$のとき,
$\angle BAE$の大きさは何度ですか.
⑩1箱60円のチョコレートと1個40円のあめが売られています.
このチョコレートとあめを買うとき,代金をちょうど500円にするには,
買い方は全部で何通りありますか.
図は動画内を参照
【受験対策】数学-証明3

単元:
#数学(中学生)#中1数学#中2数学#平行と合同#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右図のように,$\triangle ABC$の辺$BC$上に点$D$がある.
3点$A,B,D$を通る円と,辺$AC$との交点を$E$とするとき,
次の各問いに答えなさい.
①$\angle AEB=47°$のとき,$\angle ADC$の大きさを求めなさい.
②$AE=BD$のとき,$\triangle ACD\equiv \triangle BCE$を証明しなさい.
図は動画内参照
この動画を見る
右図のように,$\triangle ABC$の辺$BC$上に点$D$がある.
3点$A,B,D$を通る円と,辺$AC$との交点を$E$とするとき,
次の各問いに答えなさい.
①$\angle AEB=47°$のとき,$\angle ADC$の大きさを求めなさい.
②$AE=BD$のとき,$\triangle ACD\equiv \triangle BCE$を証明しなさい.
図は動画内参照
【受験対策】数学-証明1

単元:
#算数(中学受験)#数学(中学生)#中1数学#空間図形#平面図形#角度と面積#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右の図で,四角形$ABCD$は,$AD /\!/BC,AD\lt BC$の台形である.
辺$CD$の中点を$E$ とし,
辺$BC$の延長と$AE$の延長との交点を$F$とする.
また,頂点$B$から辺$CD$に平行にひいた直線と
$EA$の延長との交点を$G$とするとき,
次の各問いに答えなさい.
①$AE=FE$であることを証明しなさい.
②$\angle DAE=42°,\angle FEC=37$のとき,
$\angle CBG$の大きさを求めなさい.
図は動画内参照
この動画を見る
右の図で,四角形$ABCD$は,$AD /\!/BC,AD\lt BC$の台形である.
辺$CD$の中点を$E$ とし,
辺$BC$の延長と$AE$の延長との交点を$F$とする.
また,頂点$B$から辺$CD$に平行にひいた直線と
$EA$の延長との交点を$G$とするとき,
次の各問いに答えなさい.
①$AE=FE$であることを証明しなさい.
②$\angle DAE=42°,\angle FEC=37$のとき,
$\angle CBG$の大きさを求めなさい.
図は動画内参照
【受験対策】数学-図形9

単元:
#数学(中学生)#中1数学#空間図形#平面図形#角度と面積#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①右の図1で,$\ell /\!/ m$のとき,
$\angle x +\angle y$の大きさを求めなさい.
② 右の図2で,半径3cm,中心角$90°$のおうぎ形がある.
これを,辺$AC$を軸として1回転させてできる立体の表面積を求めなさい.
ただし,円周率は$\pi$を用いるものとする.
③右の図3は,直角三角形と2つの半円を組み合わせたものである.
3つの$\boxminus$部分の面積の合計を求めなさい.
ただし,円周率は$\pi$を用いるものとする.
図は動画内参照
この動画を見る
①右の図1で,$\ell /\!/ m$のとき,
$\angle x +\angle y$の大きさを求めなさい.
② 右の図2で,半径3cm,中心角$90°$のおうぎ形がある.
これを,辺$AC$を軸として1回転させてできる立体の表面積を求めなさい.
ただし,円周率は$\pi$を用いるものとする.
③右の図3は,直角三角形と2つの半円を組み合わせたものである.
3つの$\boxminus$部分の面積の合計を求めなさい.
ただし,円周率は$\pi$を用いるものとする.
図は動画内参照
【中1 数学】中1-76 おうぎ形の弧と面積② ~応用編~

単元:
#数学(中学生)#中1数学#空間図形#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①半径9cm、面積36$\pi$cm²のおうぎ形の中心角の大きさと弧の長さをもとめよう.
②半径6cm、弧の長さ9$\pi$cmのおうぎ形の中心角の大きさと面積をもとめよう.
この動画を見る
①半径9cm、面積36$\pi$cm²のおうぎ形の中心角の大きさと弧の長さをもとめよう.
②半径6cm、弧の長さ9$\pi$cmのおうぎ形の中心角の大きさと面積をもとめよう.
【受験対策】 数学-図形③
単元:
#数学(中学生)#中1数学#中3数学#相似な図形#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
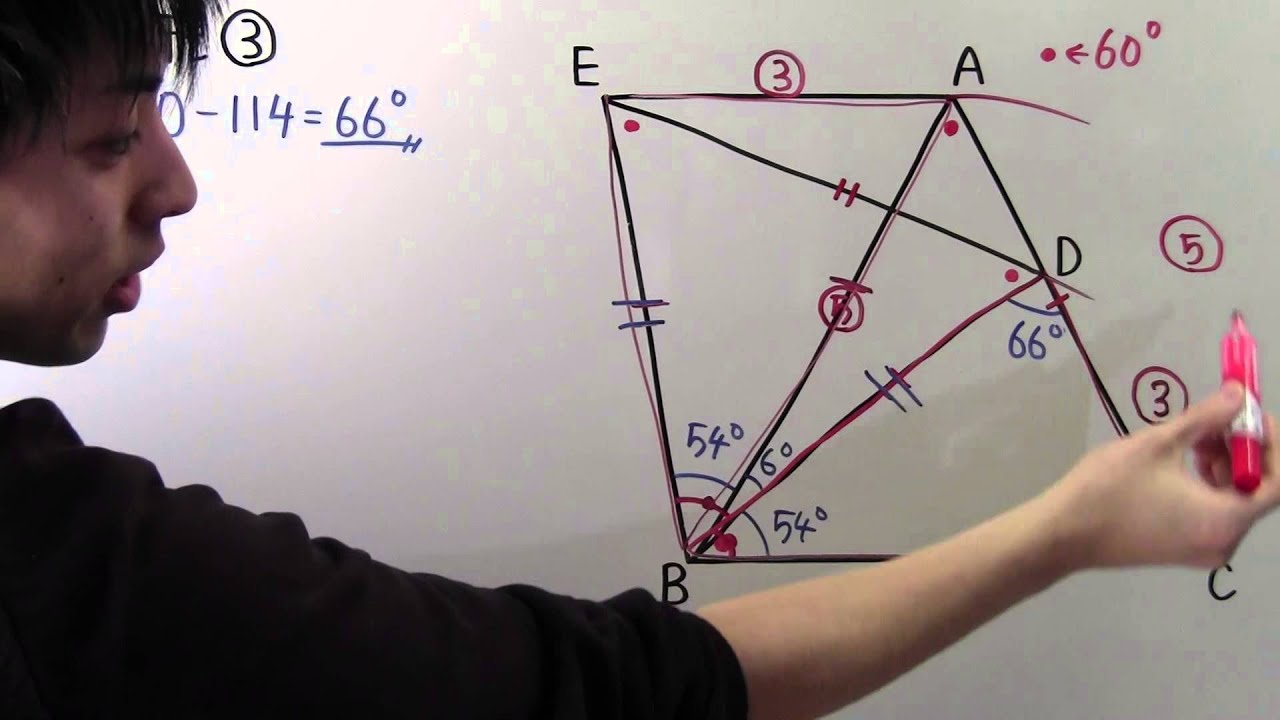
右の図で、△ABC,△BDEはどちらも正三角形で辺AC上に頂点Dがあります。
AB:AE=5:3のとき、次の問いに答えよう。
①$\angle ABE=54°$のとき、$\angle BDC$の大きさは?
②AD:CDを、最も簡単な整数の比で求めよう。
③△ABDの面積は四角形EBCAの面積の何倍?
※図は動画内参照
この動画を見る
右の図で、△ABC,△BDEはどちらも正三角形で辺AC上に頂点Dがあります。
AB:AE=5:3のとき、次の問いに答えよう。
①$\angle ABE=54°$のとき、$\angle BDC$の大きさは?
②AD:CDを、最も簡単な整数の比で求めよう。
③△ABDの面積は四角形EBCAの面積の何倍?
※図は動画内参照
【受験対策】 数学-図形②
単元:
#数学(中学生)#中1数学#中3数学#相似な図形#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①右の[図1]のような図形を組み立てて、三角柱の形をした容器をつくりました。
この容器を立てて、中に48$cm^3$の水を入れたとき、水が容器にふれている部分の面積を 求めよう。
ただし、容器の厚みは考えないものとし、水がこぼれることもないものとします。
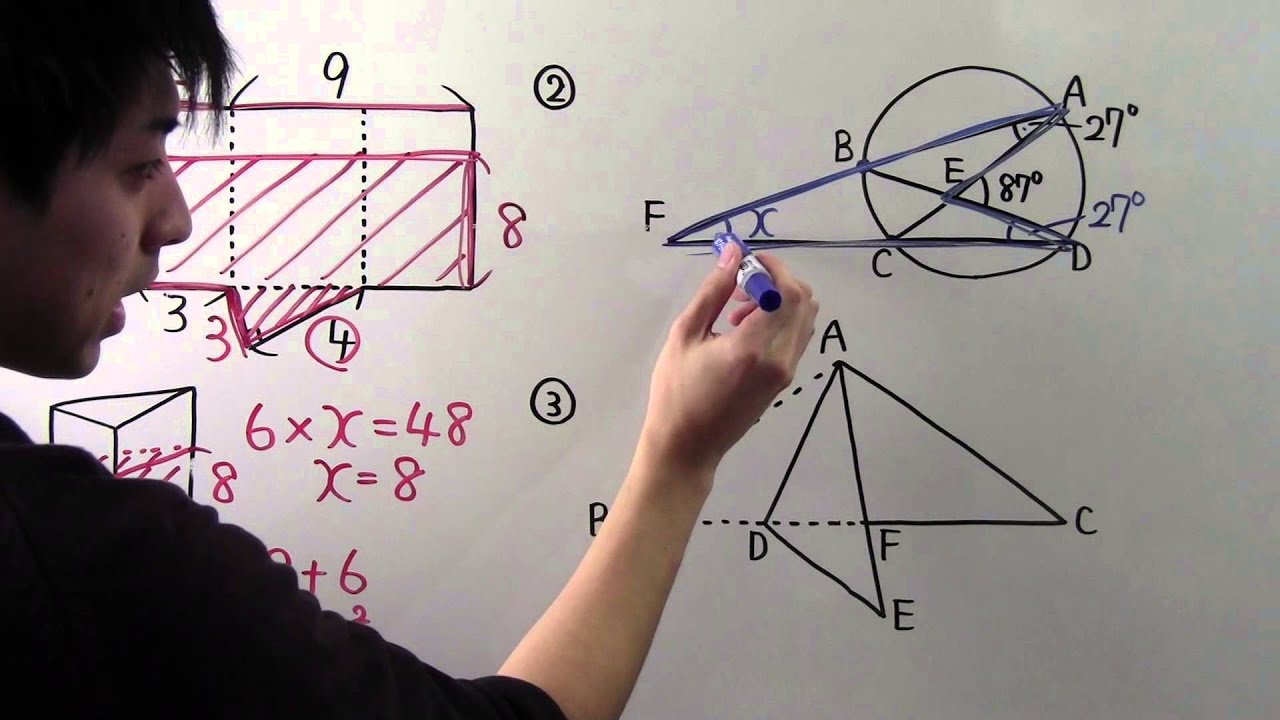
② 右の[図2]のように、円周上に点A、B、C、Dがあります。
ACとBDの交点をEとし、直線ABと直線CDの交点をF とします。
$\angle BAC=27°\angle AED=87°$のとき、 $\angle AFD$の大きさを求めよう。
③右の[図3]で、△ABCはAB=ACの二等辺三角形です。
辺BC上に点Dをとり、ADを折り目として折り返し、
頂点Bが移った位置をEとします。
辺BCとAEの交点をFと すると、FD=FEになりました。
$\angle BAD=42°$のとき、 $\angle ACB$の大きさを求めよう。
※図は動画内参照
この動画を見る
①右の[図1]のような図形を組み立てて、三角柱の形をした容器をつくりました。
この容器を立てて、中に48$cm^3$の水を入れたとき、水が容器にふれている部分の面積を 求めよう。
ただし、容器の厚みは考えないものとし、水がこぼれることもないものとします。
② 右の[図2]のように、円周上に点A、B、C、Dがあります。
ACとBDの交点をEとし、直線ABと直線CDの交点をF とします。
$\angle BAC=27°\angle AED=87°$のとき、 $\angle AFD$の大きさを求めよう。
③右の[図3]で、△ABCはAB=ACの二等辺三角形です。
辺BC上に点Dをとり、ADを折り目として折り返し、
頂点Bが移った位置をEとします。
辺BCとAEの交点をFと すると、FD=FEになりました。
$\angle BAD=42°$のとき、 $\angle ACB$の大きさを求めよう。
※図は動画内参照
【中1 数学】中1-78 おうぎ形の弧と面積④ ~さらにややこしい図形編~

単元:
#数学(中学生)#中1数学#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎色のついている部分の面積と周の長さをもとめよう!
①
[面]
[周]
②
ACを直径とする半径は、ABを直径とする
半円を点Aを中心に30°回転させたもの。
[面]
[周]
※図は動画内参照
この動画を見る
◎色のついている部分の面積と周の長さをもとめよう!
①
[面]
[周]
②
ACを直径とする半径は、ABを直径とする
半円を点Aを中心に30°回転させたもの。
[面]
[周]
※図は動画内参照
【中1 数学】中1-77 おうぎ形の弧と面積③ ~ややこしい図形編~

単元:
#数学(中学生)#中1数学#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎色のついている部分の面積と周の長さをもとめよう!
①
[面]
[周]
②
[面]
[周]
※図は動画内参照
この動画を見る
◎色のついている部分の面積と周の長さをもとめよう!
①
[面]
[周]
②
[面]
[周]
※図は動画内参照
(撮り直し前)【中1 数学】 中1-76 おうぎ形の弧と面積② ・ 応用編

単元:
#数学(中学生)#中1数学#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①半径9cm、面積36π$cm^2$のおうぎ形の中心角の大きさと弧の長さをもとめよう!
②半径6cm、弧の長さ9πcmのおうぎ形の中心角の大きさと面積をもとめよう!
この動画を見る
①半径9cm、面積36π$cm^2$のおうぎ形の中心角の大きさと弧の長さをもとめよう!
②半径6cm、弧の長さ9πcmのおうぎ形の中心角の大きさと面積をもとめよう!
【中1 数学】中1-75 おうぎ形の弧と面積① ~基本編~

単元:
#数学(中学生)#中1数学#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
[円]
面積=①________
円周=②________
[おうぎ形]
面積=③________
弧=④________
◎半径12cm、中心角60°のおうぎ形について。
⑤面積は?
⑥弧の長さは?
◎半径5cm、中心角144°のおうぎ形について。
⑦面積は?
⑧弧の長さは?
この動画を見る
[円]
面積=①________
円周=②________
[おうぎ形]
面積=③________
弧=④________
◎半径12cm、中心角60°のおうぎ形について。
⑤面積は?
⑥弧の長さは?
◎半径5cm、中心角144°のおうぎ形について。
⑦面積は?
⑧弧の長さは?
【中1 数学】中1-74 円とおうぎ形の性質③ ~おうぎ形編~
単元:
#数学(中学生)#中1数学#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
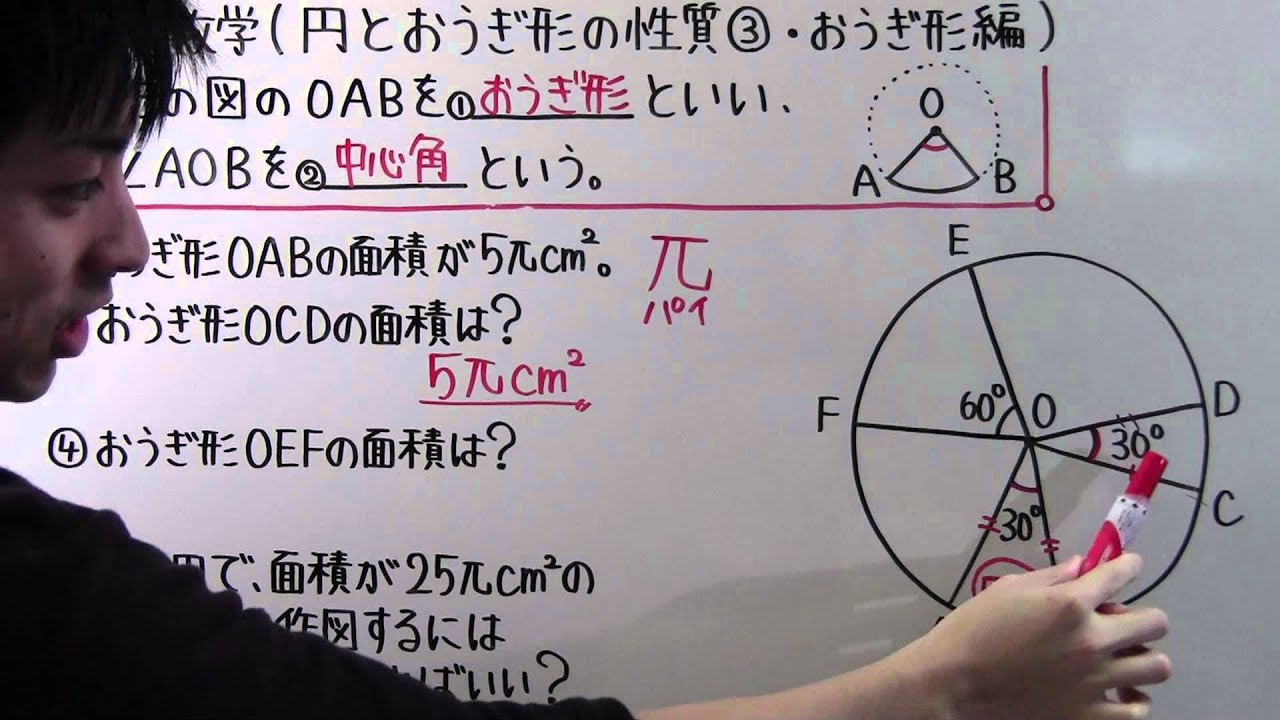
右の図のOABを①____といい、
$\angle AOB$を②____という。
◎おうぎ形OABの面積が$5πcm^2$。
③おうぎ形OCDの面積は?
④おうぎ形OEFの面積は?
⑤右の円で、面積が$25πcm^2$のおうぎ形を作図するには
中心角を何度にすればいい?
※図は動画内参照
この動画を見る
右の図のOABを①____といい、
$\angle AOB$を②____という。
◎おうぎ形OABの面積が$5πcm^2$。
③おうぎ形OCDの面積は?
④おうぎ形OEFの面積は?
⑤右の円で、面積が$25πcm^2$のおうぎ形を作図するには
中心角を何度にすればいい?
※図は動画内参照
【中1 数学】中1-73 円とおうぎ形の性質② ~作図編~

単元:
#数学(中学生)#中1数学#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①点Aが接点となるように接線ℓを作図しよう!
②中心が直線m上にあって点Aで直線ℓに接する円を作図しよう!
③割れた円形の皿の中心Oを作図しよう!
④点Aで直線OYに接して、かつ直線OXにも接する円を作図しよう!
※図は動画内参照
この動画を見る
①点Aが接点となるように接線ℓを作図しよう!
②中心が直線m上にあって点Aで直線ℓに接する円を作図しよう!
③割れた円形の皿の中心Oを作図しよう!
④点Aで直線OYに接して、かつ直線OXにも接する円を作図しよう!
※図は動画内参照
【中1 数学】中1-72 円とおうぎ形の性質① ~基本編~

単元:
#数学(中学生)#中1数学#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
$\boxed{Ⅰ}$の図で、線分ABを①____、円周のAからBまでの部分を②____といい、③____とかく。
また、$\angle AOB$を③‗‗‗‗‗‗に対する④____といい、
線分ABが直径なら、④‗‗‗‗‗‗は⑤____になる。
$\boxed{Ⅱ}$の図のように、円と直線が1点で交わるとき、直線は円に⑥____という。
そして、このときの点Cを⑦____、直線ℓを⑧____といい、OCはℓに⑨____になる!
※図は動画内参照
この動画を見る
$\boxed{Ⅰ}$の図で、線分ABを①____、円周のAからBまでの部分を②____といい、③____とかく。
また、$\angle AOB$を③‗‗‗‗‗‗に対する④____といい、
線分ABが直径なら、④‗‗‗‗‗‗は⑤____になる。
$\boxed{Ⅱ}$の図のように、円と直線が1点で交わるとき、直線は円に⑥____という。
そして、このときの点Cを⑦____、直線ℓを⑧____といい、OCはℓに⑨____になる!
※図は動画内参照
【中1 数学】中1-71 作図③ ~さらに応用編~
単元:
#数学(中学生)#中1数学#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
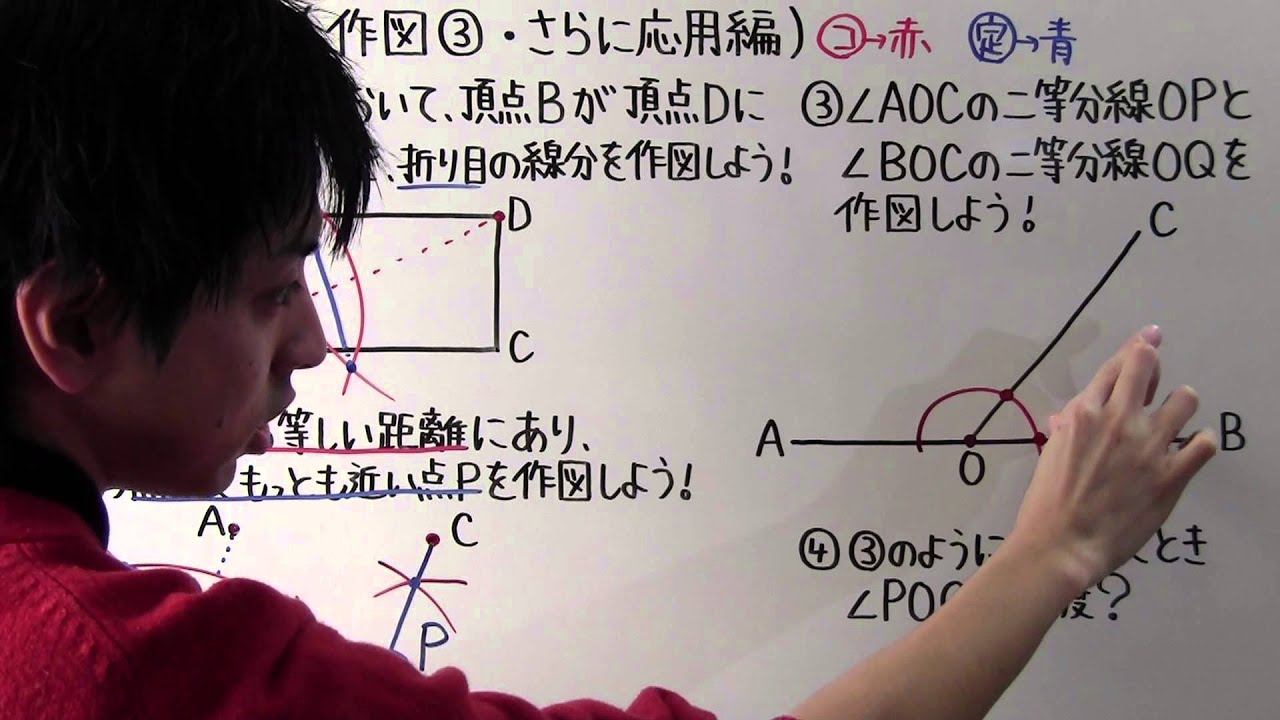
①長方形ABCDにおいて、頂点Bが頂点Dに重なるように折るとき、折り目の線分を作図しよう!
②2点A,Bから等しい距離にあり、かつ点Cに最も近い点Pを作図しよう!
③$\angle AOC$の二等分線OPと$\angle BOC$の二等分線OQを作図しよう!
④③のように作図したとき$\angle POQ$は何度?
※図は動画内参照
この動画を見る
①長方形ABCDにおいて、頂点Bが頂点Dに重なるように折るとき、折り目の線分を作図しよう!
②2点A,Bから等しい距離にあり、かつ点Cに最も近い点Pを作図しよう!
③$\angle AOC$の二等分線OPと$\angle BOC$の二等分線OQを作図しよう!
④③のように作図したとき$\angle POQ$は何度?
※図は動画内参照
【中1 数学】中1-70 作図② ~応用編~
単元:
#数学(中学生)#中1数学#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
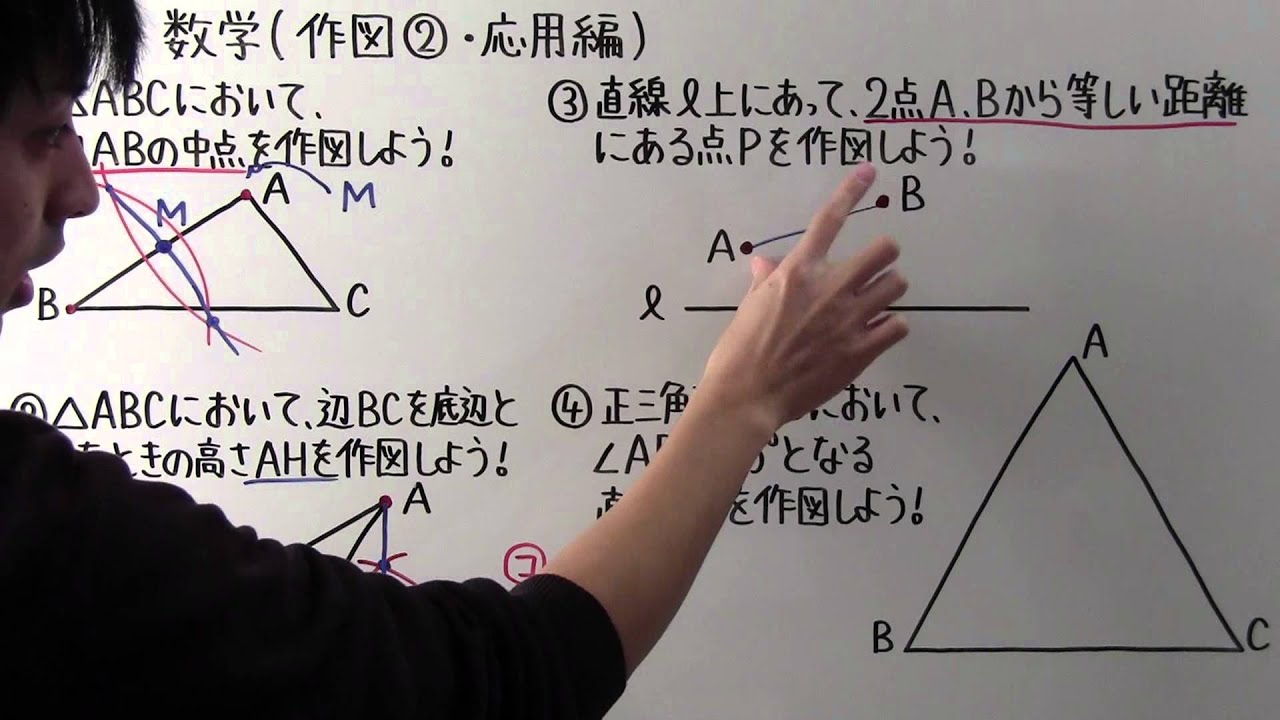
①△ABCにおいて、辺ABの中点を作図しよう!
②△ABCにおいて、辺BCを底辺としたときの高さAHを作図しよう!
③直線ℓ上にあって、2点A,Bから等しい距離にある点Pを作図しよう!
④正三角形ABCにおいて、
$\angle ABD=15°$となる直線BDを作図しよう!
※図は動画内参照
この動画を見る
①△ABCにおいて、辺ABの中点を作図しよう!
②△ABCにおいて、辺BCを底辺としたときの高さAHを作図しよう!
③直線ℓ上にあって、2点A,Bから等しい距離にある点Pを作図しよう!
④正三角形ABCにおいて、
$\angle ABD=15°$となる直線BDを作図しよう!
※図は動画内参照
【中1 数学】中1-69 作図① ~基本編~

単元:
#数学(中学生)#中1数学#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎それぞれの作図をして、効果を書こう!
$\boxed{1}$垂直二等分線
①
【効果】
作図した線分ABと②____になるし、その交点は線分ABの③____になる。
つまり、2点A,Bから④____にあるってこと!
$\boxed{2}$角の二等分線
⑤
【効果】
その角を⑥____にする。
OX,OYから、⑦____にある!
$\boxed{3}$点Pを通る垂線(2種類)
⑧
⑨
【効果】
⑩____を通る⑪____な線が書ける。
また、距離が⑩________線を書くときに使う!
※図は動画内参照
この動画を見る
◎それぞれの作図をして、効果を書こう!
$\boxed{1}$垂直二等分線
①
【効果】
作図した線分ABと②____になるし、その交点は線分ABの③____になる。
つまり、2点A,Bから④____にあるってこと!
$\boxed{2}$角の二等分線
⑤
【効果】
その角を⑥____にする。
OX,OYから、⑦____にある!
$\boxed{3}$点Pを通る垂線(2種類)
⑧
⑨
【効果】
⑩____を通る⑪____な線が書ける。
また、距離が⑩________線を書くときに使う!
※図は動画内参照
【中1 数学】中1-68 図形の移動③ ~作図編~
単元:
#数学(中学生)#中1数学#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
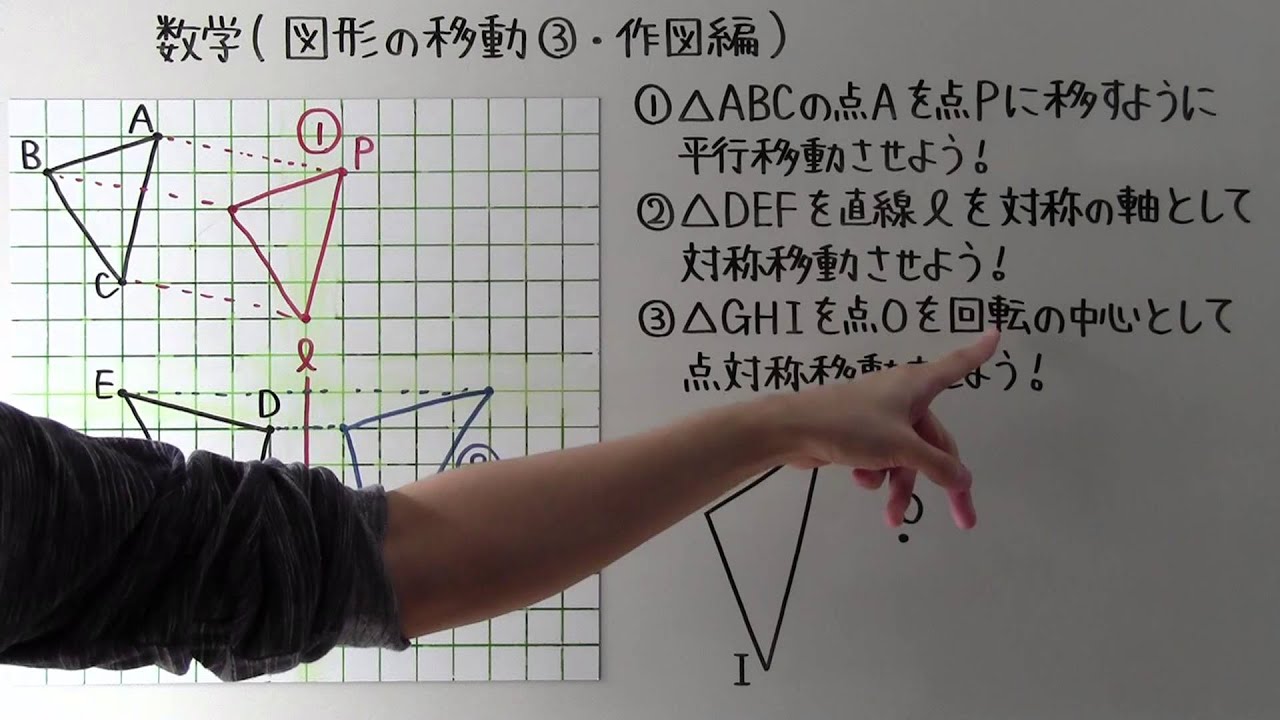
①△ABCの点Aを点Pに移すように平行移動させよう!
②△DEFを直線ℓを対称軸として対称移動させよう!
③△GHIを点Oを回転の中心として点対称移動させよう!
※図は動画内参照
この動画を見る
①△ABCの点Aを点Pに移すように平行移動させよう!
②△DEFを直線ℓを対称軸として対称移動させよう!
③△GHIを点Oを回転の中心として点対称移動させよう!
※図は動画内参照
【中1 数学】中1-67 図形の移動② ~問題編~

単元:
#数学(中学生)#中1数学#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①㋑を平行移動して重なるのは?
②△OAEを平行移動して重なるのは?
③㋖をHFを対称の軸として対称移動して重なるのは?
④△OAEを点Oを回転の中心として回転移動して重なるものをすべて書こう!
⑤△ODGを点Oを回転の中心として、反時計回りに90°回転移動し、さらにEGを対称の軸として対称移動して重なるのは?
※図は動画内参照
この動画を見る
①㋑を平行移動して重なるのは?
②△OAEを平行移動して重なるのは?
③㋖をHFを対称の軸として対称移動して重なるのは?
④△OAEを点Oを回転の中心として回転移動して重なるものをすべて書こう!
⑤△ODGを点Oを回転の中心として、反時計回りに90°回転移動し、さらにEGを対称の軸として対称移動して重なるのは?
※図は動画内参照
【中1 数学】中1-65 直線と角② ~問題編~
単元:
#数学(中学生)#中1数学#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎台形ABCDについて!
①平行な線分を記号を使って表すと?
②垂直な線分を記号を使って表すと?
③点Dと線分BCとの距離は何㎝?
※図は動画内参照
◎次の三角形を書こう!
④$AB=4cm,BC=6cm,CA=5cm$
⑤$BC=7cm,\angle ABC=40°,\angle ACB=60°$
この動画を見る
◎台形ABCDについて!
①平行な線分を記号を使って表すと?
②垂直な線分を記号を使って表すと?
③点Dと線分BCとの距離は何㎝?
※図は動画内参照
◎次の三角形を書こう!
④$AB=4cm,BC=6cm,CA=5cm$
⑤$BC=7cm,\angle ABC=40°,\angle ACB=60°$
