 中1数学
中1数学
 中1数学
中1数学
【高校受験対策】数学-死守8

単元:
#中1数学#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根#文章題#文章題その他#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$4 \times (5+2)$を計算しなさい.
②$\dfrac{2}{3}-\dfrac{1}{5}$を計算しなさい.
③$24\div (-6)$を計算しなさい.
④$3(2x-y)-(x+5y)$を計算しなさい.
⑤連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+3y=8 \\
2x-y=-5
\end{array}
\right.
\end{eqnarray}$を解きなさい.
⑥$x^2+x-56$を因数分解しなさい.
⑦$(\sqrt{27}-\sqrt3)\times \sqrt2$を計算しなさい.
⑧方程式$x^2-5x+1=0$を解きなさい.
⑨下の図のように,$\triangle ABC$の辺$BC$を延長して$CD$とし,
辺$CA$を延長して$AE$とします.
$\angle ABC=41°,\angle ACD=124°$のとき,
$\angle BAE$の大きさは何度ですか.
⑩1箱60円のチョコレートと1個40円のあめが売られています.
このチョコレートとあめを買うとき,代金をちょうど500円にするには,
買い方は全部で何通りありますか.
図は動画内を参照
この動画を見る
①$4 \times (5+2)$を計算しなさい.
②$\dfrac{2}{3}-\dfrac{1}{5}$を計算しなさい.
③$24\div (-6)$を計算しなさい.
④$3(2x-y)-(x+5y)$を計算しなさい.
⑤連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+3y=8 \\
2x-y=-5
\end{array}
\right.
\end{eqnarray}$を解きなさい.
⑥$x^2+x-56$を因数分解しなさい.
⑦$(\sqrt{27}-\sqrt3)\times \sqrt2$を計算しなさい.
⑧方程式$x^2-5x+1=0$を解きなさい.
⑨下の図のように,$\triangle ABC$の辺$BC$を延長して$CD$とし,
辺$CA$を延長して$AE$とします.
$\angle ABC=41°,\angle ACD=124°$のとき,
$\angle BAE$の大きさは何度ですか.
⑩1箱60円のチョコレートと1個40円のあめが売られています.
このチョコレートとあめを買うとき,代金をちょうど500円にするには,
買い方は全部で何通りありますか.
図は動画内を参照
【高校受験対策】数学-死守6

単元:
#数学(中学生)#中1数学#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#連立方程式#2次方程式#比例・反比例#円
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
1.次の計算をしなさい.
①$5-7$
②$- 6 + 9 \div \dfrac{1}{4}$
③$3\sqrt2\times \sqrt8$
④$2(2a-3b)+(a-5b)$
2.次の問いに答えなさい.
⑤右の図1のように,線分$AB$を直径とする円があります.
円の中心$O$を定規とコンパスを使って作図しなさい.
ただし,点を示す記号$O$をかき入れ,作図に用いた線は消さないこと.
⑥右の図2のような反比例の関係$y =\dfrac{a}{x}$のグラフがあります.
点$O$は原点とします.$a$の値を求めなさい.
⑦連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x + y = 5 \\
y=4x-1
\end{array}
\right.
\end{eqnarray}$を解きなさい.
⑧二次方程式$x^2+5x+1=0$を解きなさい.
図は動画内を参照
この動画を見る
1.次の計算をしなさい.
①$5-7$
②$- 6 + 9 \div \dfrac{1}{4}$
③$3\sqrt2\times \sqrt8$
④$2(2a-3b)+(a-5b)$
2.次の問いに答えなさい.
⑤右の図1のように,線分$AB$を直径とする円があります.
円の中心$O$を定規とコンパスを使って作図しなさい.
ただし,点を示す記号$O$をかき入れ,作図に用いた線は消さないこと.
⑥右の図2のような反比例の関係$y =\dfrac{a}{x}$のグラフがあります.
点$O$は原点とします.$a$の値を求めなさい.
⑦連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x + y = 5 \\
y=4x-1
\end{array}
\right.
\end{eqnarray}$を解きなさい.
⑧二次方程式$x^2+5x+1=0$を解きなさい.
図は動画内を参照
【高校受験対策】数学-死守4

単元:
#数学(中学生)#中1数学#中2数学#中3数学#方程式#式の計算(単項式・多項式・式の四則計算)#2次方程式#比例・反比例
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の各問に答えよ.
①$7+3\times (-5)$を計算せよ.
②$3(2a+1)-4(a+2)$を計算せよ.
③$a=-3,b=6$のとき,
$-a^2+2b$の値を求めよ.
④$\dfrac{27}{\sqrt3}-\sqrt{48}$を計算せよ.
⑤1次方程式$x-9=3(x-1)$を解け.
⑥2次方程式$x(x-6)=-4(x-2)$を解け.
⑦$y$は$x$に反比例し,$x=-3$のとき,$y=-8$である.
$x=-4$のときの$y$の値を求めよ.
この動画を見る
次の各問に答えよ.
①$7+3\times (-5)$を計算せよ.
②$3(2a+1)-4(a+2)$を計算せよ.
③$a=-3,b=6$のとき,
$-a^2+2b$の値を求めよ.
④$\dfrac{27}{\sqrt3}-\sqrt{48}$を計算せよ.
⑤1次方程式$x-9=3(x-1)$を解け.
⑥2次方程式$x(x-6)=-4(x-2)$を解け.
⑦$y$は$x$に反比例し,$x=-3$のとき,$y=-8$である.
$x=-4$のときの$y$の値を求めよ.
【高校受験対策】死守-3

単元:
#数学(中学生)#中1数学#中2数学#中3数学#方程式#式の計算(単項式・多項式・式の四則計算)#連立方程式#2次方程式#1次関数#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の各問に答えよ.
①$6+4 \times \left(-\dfrac{1}{2}\right)$を計算せよ.
②$8a+b-(a-7b)$を計算せよ.
③$(\sqrt5 +\sqrt 3)(\sqrt 5-\sqrt3)$を計算せよ.
④1次方程式$9x+2=8(x+1)$を解け.
⑤連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x+y=4 \\
6x+5y=-7
\end{array}
\right.
\end{eqnarray}$を解け.
⑥2次方程式$x^2-8x-9=0$を解け.
⑦関数$y=\dfrac{1}{3}x^2$について,
$x$の値を3から9まで増加するときの割合を求めよ.
この動画を見る
次の各問に答えよ.
①$6+4 \times \left(-\dfrac{1}{2}\right)$を計算せよ.
②$8a+b-(a-7b)$を計算せよ.
③$(\sqrt5 +\sqrt 3)(\sqrt 5-\sqrt3)$を計算せよ.
④1次方程式$9x+2=8(x+1)$を解け.
⑤連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x+y=4 \\
6x+5y=-7
\end{array}
\right.
\end{eqnarray}$を解け.
⑥2次方程式$x^2-8x-9=0$を解け.
⑦関数$y=\dfrac{1}{3}x^2$について,
$x$の値を3から9まで増加するときの割合を求めよ.
【高校受験対策】死守-1

単元:
#数学(中学生)#中1数学#中2数学#中3数学#方程式#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#2次方程式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$24 \div (7-4)$を計算しなさい.
②$\dfrac{1}{2}+\dfrac{2}{5}$を計算しなさい.
③$7+(-3)\times 4$を計算しなさい.
④$(5x-y)-3(x-5y)$を計算しなさい.
⑤下の連立方程式を解きなさい.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x = 3y-2 \\
4x-7y=2
\end{array}
\right.
\end{eqnarray}$
⑥$\sqrt{32}-\sqrt 8+\sqrt2 $を計算しなさい.
⑦$x^2-36y^2$を因数分解しなさい.
⑧方程式$x^2+7x+2=0$を解きなさい.
この動画を見る
①$24 \div (7-4)$を計算しなさい.
②$\dfrac{1}{2}+\dfrac{2}{5}$を計算しなさい.
③$7+(-3)\times 4$を計算しなさい.
④$(5x-y)-3(x-5y)$を計算しなさい.
⑤下の連立方程式を解きなさい.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x = 3y-2 \\
4x-7y=2
\end{array}
\right.
\end{eqnarray}$
⑥$\sqrt{32}-\sqrt 8+\sqrt2 $を計算しなさい.
⑦$x^2-36y^2$を因数分解しなさい.
⑧方程式$x^2+7x+2=0$を解きなさい.
【受験対策】数学-図形11

単元:
#数学(中学生)#中1数学#空間図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右の図は,$ AB = 3cm,BC = 2cm,\angle ABC = 90°$の
直角三角形$ABC$を底面とし,
点$D$を頂点とする三角錐であり,
$AD=6cm,\angle ABD= \angle CBD = 90°$である.
また,点$E$は辺$AD$上の点で,$AE = 2cm$である.
このとき,次の各問いに答えなさい.
①この三角錐の体積を求めなさい.
②この三角錐の表面に,点$C$から辺$BD$を通るように,
点$E$まで細い糸をかける.
かけた糸の長さが最も短くなるとき,その糸の長さを求めなさい.
ただし糸はのびたり縮んだりしないものとする.
図は動画内参照
この動画を見る
右の図は,$ AB = 3cm,BC = 2cm,\angle ABC = 90°$の
直角三角形$ABC$を底面とし,
点$D$を頂点とする三角錐であり,
$AD=6cm,\angle ABD= \angle CBD = 90°$である.
また,点$E$は辺$AD$上の点で,$AE = 2cm$である.
このとき,次の各問いに答えなさい.
①この三角錐の体積を求めなさい.
②この三角錐の表面に,点$C$から辺$BD$を通るように,
点$E$まで細い糸をかける.
かけた糸の長さが最も短くなるとき,その糸の長さを求めなさい.
ただし糸はのびたり縮んだりしないものとする.
図は動画内参照
【受験対策】数学-証明3

単元:
#数学(中学生)#中1数学#中2数学#平行と合同#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右図のように,$\triangle ABC$の辺$BC$上に点$D$がある.
3点$A,B,D$を通る円と,辺$AC$との交点を$E$とするとき,
次の各問いに答えなさい.
①$\angle AEB=47°$のとき,$\angle ADC$の大きさを求めなさい.
②$AE=BD$のとき,$\triangle ACD\equiv \triangle BCE$を証明しなさい.
図は動画内参照
この動画を見る
右図のように,$\triangle ABC$の辺$BC$上に点$D$がある.
3点$A,B,D$を通る円と,辺$AC$との交点を$E$とするとき,
次の各問いに答えなさい.
①$\angle AEB=47°$のとき,$\angle ADC$の大きさを求めなさい.
②$AE=BD$のとき,$\triangle ACD\equiv \triangle BCE$を証明しなさい.
図は動画内参照
【受験対策】数学-証明1

単元:
#算数(中学受験)#数学(中学生)#中1数学#空間図形#平面図形#角度と面積#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右の図で,四角形$ABCD$は,$AD /\!/BC,AD\lt BC$の台形である.
辺$CD$の中点を$E$ とし,
辺$BC$の延長と$AE$の延長との交点を$F$とする.
また,頂点$B$から辺$CD$に平行にひいた直線と
$EA$の延長との交点を$G$とするとき,
次の各問いに答えなさい.
①$AE=FE$であることを証明しなさい.
②$\angle DAE=42°,\angle FEC=37$のとき,
$\angle CBG$の大きさを求めなさい.
図は動画内参照
この動画を見る
右の図で,四角形$ABCD$は,$AD /\!/BC,AD\lt BC$の台形である.
辺$CD$の中点を$E$ とし,
辺$BC$の延長と$AE$の延長との交点を$F$とする.
また,頂点$B$から辺$CD$に平行にひいた直線と
$EA$の延長との交点を$G$とするとき,
次の各問いに答えなさい.
①$AE=FE$であることを証明しなさい.
②$\angle DAE=42°,\angle FEC=37$のとき,
$\angle CBG$の大きさを求めなさい.
図は動画内参照
【受験対策】数学-図形9

単元:
#数学(中学生)#中1数学#空間図形#平面図形#角度と面積#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①右の図1で,$\ell /\!/ m$のとき,
$\angle x +\angle y$の大きさを求めなさい.
② 右の図2で,半径3cm,中心角$90°$のおうぎ形がある.
これを,辺$AC$を軸として1回転させてできる立体の表面積を求めなさい.
ただし,円周率は$\pi$を用いるものとする.
③右の図3は,直角三角形と2つの半円を組み合わせたものである.
3つの$\boxminus$部分の面積の合計を求めなさい.
ただし,円周率は$\pi$を用いるものとする.
図は動画内参照
この動画を見る
①右の図1で,$\ell /\!/ m$のとき,
$\angle x +\angle y$の大きさを求めなさい.
② 右の図2で,半径3cm,中心角$90°$のおうぎ形がある.
これを,辺$AC$を軸として1回転させてできる立体の表面積を求めなさい.
ただし,円周率は$\pi$を用いるものとする.
③右の図3は,直角三角形と2つの半円を組み合わせたものである.
3つの$\boxminus$部分の面積の合計を求めなさい.
ただし,円周率は$\pi$を用いるものとする.
図は動画内参照
【中1 P.28】1編の力だめし

【中1 P.27】正負の数の計算特訓②
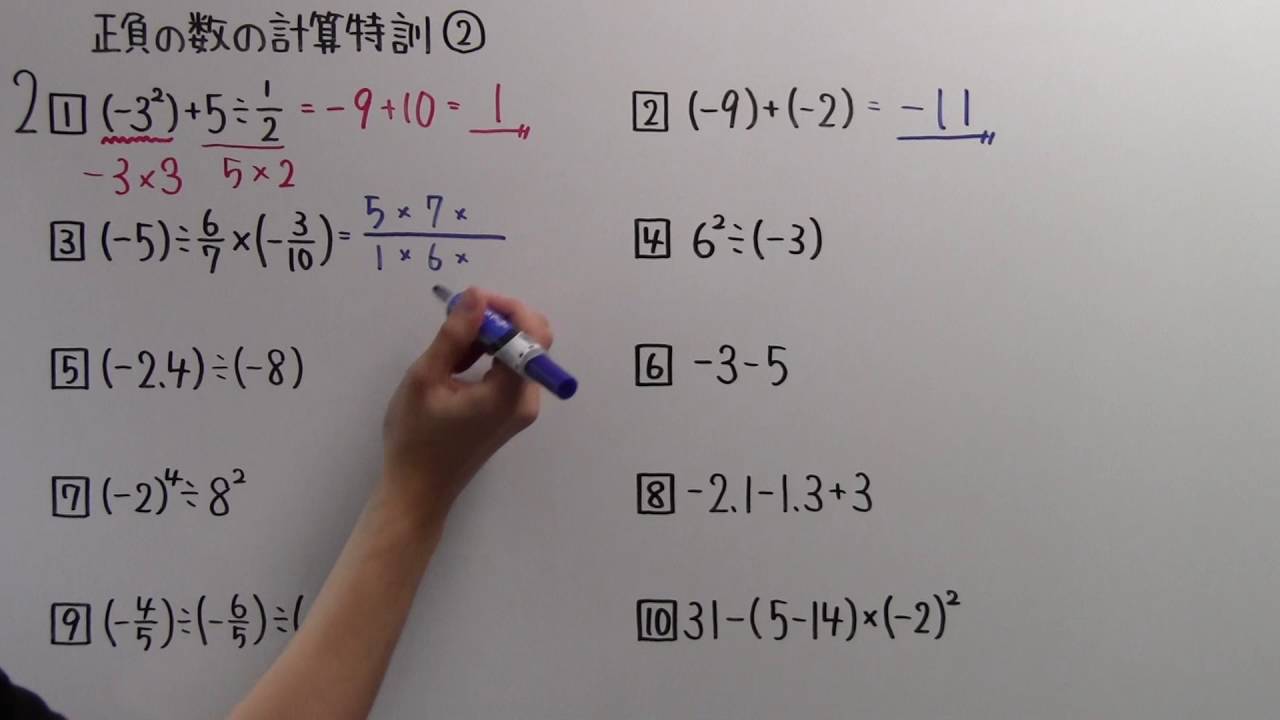
単元:
#数学(中学生)#中1数学#正の数・負の数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
2.次の計算をしよう.
$\boxed{1} \quad (-3^2)+5\div \dfrac{1}{2}$
$\boxed{2} \quad (-9)+(-2)$
$boxed{3} \quad (-5)\div \dfrac{6}{7} \times \left(-\dfrac{3}{10}\right)$
$\boxed{4} \quad 6^2\div (-3)$
$\boxed{5} \quad (-2.4)\div (-8)$
$\boxed{6} \quad -3-5$
$\boxed{7} \quad (-2)^4\div 8^2$
$\boxed{8} \quad -2.1-1.3+3$
$\boxed{9} \quad \left(-\dfrac{4}{5}\right)\div \left(-\dfrac{6}{5}\right)\div \left(-\dfrac{8}{9}\right)$
$\boxed{10} \quad 31-(5-14)\times (-2)^2$
この動画を見る
2.次の計算をしよう.
$\boxed{1} \quad (-3^2)+5\div \dfrac{1}{2}$
$\boxed{2} \quad (-9)+(-2)$
$boxed{3} \quad (-5)\div \dfrac{6}{7} \times \left(-\dfrac{3}{10}\right)$
$\boxed{4} \quad 6^2\div (-3)$
$\boxed{5} \quad (-2.4)\div (-8)$
$\boxed{6} \quad -3-5$
$\boxed{7} \quad (-2)^4\div 8^2$
$\boxed{8} \quad -2.1-1.3+3$
$\boxed{9} \quad \left(-\dfrac{4}{5}\right)\div \left(-\dfrac{6}{5}\right)\div \left(-\dfrac{8}{9}\right)$
$\boxed{10} \quad 31-(5-14)\times (-2)^2$
【中1 P.94】方程式の計算特訓①

単元:
#数学(中学生)#中1数学#方程式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
1.次の計算をしよう.
$\boxed{1} \quad 5x+4=3x+12$
$\boxed{2} \quad 9-x=5$
$\boxed{3} \quad 3(x-4)=5x+2$
$\boxed{4} \quad \dfrac{3}{2}x-1=4-x$
$\boxed{5} \quad \dfrac{x+4}{3}+1=\dfrac{3x-7}{2}$
$\boxed{6} \quad 0.4x+0.5=2.6-0.3x$
$\boxed{7} \quad 1.5x-3=\dfrac{6}{5}x-0.3$
$\boxed{8} \quad \dfrac{1}{2}x+\dfrac{3}{4}=\dfrac{3}{8}x-\dfrac{1}{2}$
この動画を見る
1.次の計算をしよう.
$\boxed{1} \quad 5x+4=3x+12$
$\boxed{2} \quad 9-x=5$
$\boxed{3} \quad 3(x-4)=5x+2$
$\boxed{4} \quad \dfrac{3}{2}x-1=4-x$
$\boxed{5} \quad \dfrac{x+4}{3}+1=\dfrac{3x-7}{2}$
$\boxed{6} \quad 0.4x+0.5=2.6-0.3x$
$\boxed{7} \quad 1.5x-3=\dfrac{6}{5}x-0.3$
$\boxed{8} \quad \dfrac{1}{2}x+\dfrac{3}{4}=\dfrac{3}{8}x-\dfrac{1}{2}$
【中1 P.95】方程式の計算特訓②

単元:
#数学(中学生)#中1数学#方程式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
2.次の計算をしよう.
$\boxed{1} \quad x:5=8:2$
$\boxed{2} \quad 3:x=7:3$
$\boxed{3} \quad (x-5):3=16:12$
$\boxed{4} \quad 2:x=3:(x+5)$
$\boxed{5} \quad (x+7):6=x:\dfrac{5}{2}$
$\boxed{6} \quad (x-2):3=(x+1):5$
この動画を見る
2.次の計算をしよう.
$\boxed{1} \quad x:5=8:2$
$\boxed{2} \quad 3:x=7:3$
$\boxed{3} \quad (x-5):3=16:12$
$\boxed{4} \quad 2:x=3:(x+5)$
$\boxed{5} \quad (x+7):6=x:\dfrac{5}{2}$
$\boxed{6} \quad (x-2):3=(x+1):5$
【中1 P.96】3編の力だめし
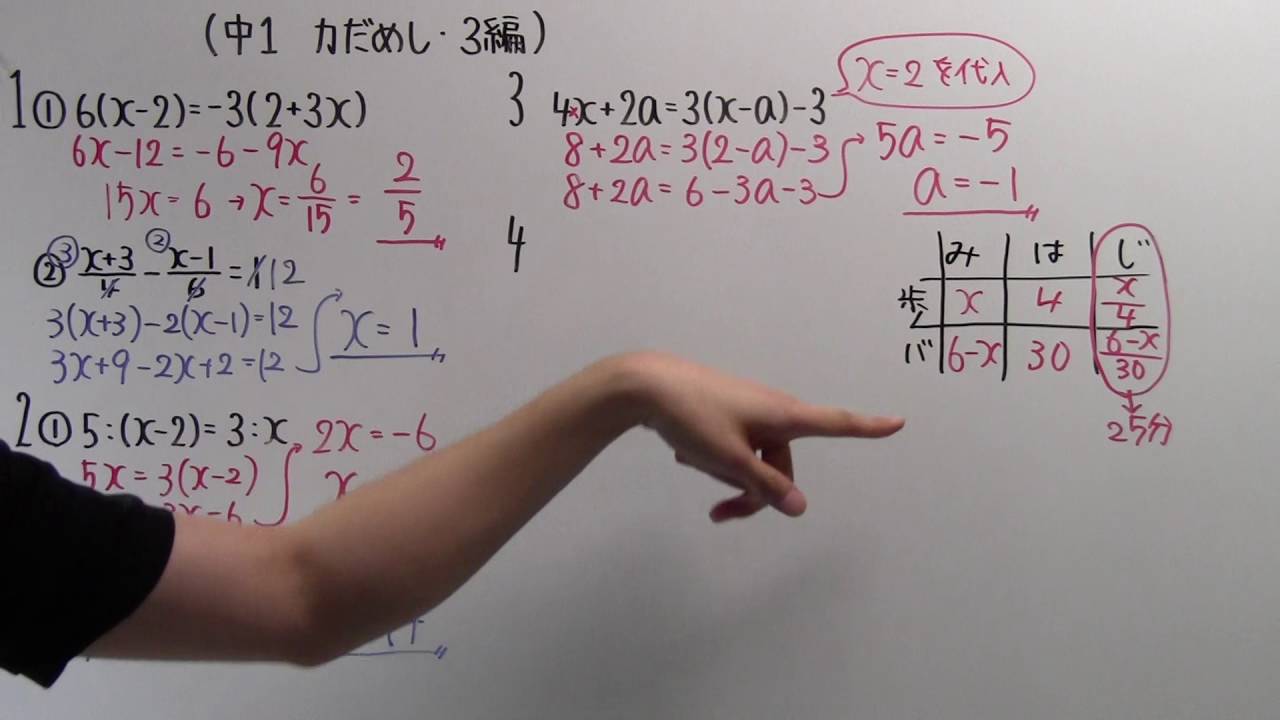
単元:
#数学(中学生)#中1数学#中2数学#式の計算(単項式・多項式・式の四則計算)#比例・反比例
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の計算をしよう.
1.①$6(x-2)=-3(2+3x)$
②$\dfrac{x+3}{4}-\dfrac{x-1}{6}=1$
2.①$5:(x-2)=3:x$
②$5:x=\dfrac{1}{4}:\dfrac{7}{10}$
3.$4x+2a-3(x-a)-3$
この動画を見る
次の計算をしよう.
1.①$6(x-2)=-3(2+3x)$
②$\dfrac{x+3}{4}-\dfrac{x-1}{6}=1$
2.①$5:(x-2)=3:x$
②$5:x=\dfrac{1}{4}:\dfrac{7}{10}$
3.$4x+2a-3(x-a)-3$
【中1 P.26】正負の数の計算特訓①

単元:
#数学(中学生)#中1数学#正の数・負の数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
1.次の数を計算しなさい.
$\boxed{1} \quad -5-(-12)$
$\boxed{2} \quad 2\times \left(-\dfrac{5}{6}\right)$
$\boxed{3} \quad 3^2+(-2)\times (-4)$
$\boxed{4} \quad -\dfrac{2}{3}\div \dfrac{1}{6}$
$\boxed{5} \quad 14-(5-21)\div (-4)$
$\boxed{6} \quad (-6)\div (-0.2)$
$\boxed{7} \quad -3+9-(-6)$
$\boxed{8} \quad \dfrac{3}{8}-\dfrac{5}{6}$
$\boxed{9} \quad 3\times (-2)^2$
$\boxed{10} \quad -9-2+11$
この動画を見る
1.次の数を計算しなさい.
$\boxed{1} \quad -5-(-12)$
$\boxed{2} \quad 2\times \left(-\dfrac{5}{6}\right)$
$\boxed{3} \quad 3^2+(-2)\times (-4)$
$\boxed{4} \quad -\dfrac{2}{3}\div \dfrac{1}{6}$
$\boxed{5} \quad 14-(5-21)\div (-4)$
$\boxed{6} \quad (-6)\div (-0.2)$
$\boxed{7} \quad -3+9-(-6)$
$\boxed{8} \quad \dfrac{3}{8}-\dfrac{5}{6}$
$\boxed{9} \quad 3\times (-2)^2$
$\boxed{10} \quad -9-2+11$
【中1 数学】中1-76 おうぎ形の弧と面積② ~応用編~

単元:
#数学(中学生)#中1数学#空間図形#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①半径9cm、面積36$\pi$cm²のおうぎ形の中心角の大きさと弧の長さをもとめよう.
②半径6cm、弧の長さ9$\pi$cmのおうぎ形の中心角の大きさと面積をもとめよう.
この動画を見る
①半径9cm、面積36$\pi$cm²のおうぎ形の中心角の大きさと弧の長さをもとめよう.
②半径6cm、弧の長さ9$\pi$cmのおうぎ形の中心角の大きさと面積をもとめよう.
【受験対策】数学-資料の活用③

単元:
#数学(中学生)#中1数学#資料の活用
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎ある年の7月に、野球チームA、Bがそれぞれ試合を行った。
右の図は、Aチームが行った全試合におけるそれぞれの得点の記録をヒストグラムに表したものである。
また、表は、Bチームが行った全試合におけるそれぞれの得点の記録を度数分布表にまとめたものであり、Bチームが行った全試合の得点の合計は108点である。
このとき、①~③に答えよう。
①図における中央値を求めよう。
②表の中の(i),(ii)にあてはまる数を求めよう。
③図、表からわかることとして正しいものを次の㋐~㋔の中から2つ選ぼう。
㋐Aチームの試合数はBチームの試合数より多く、Aチームの全試合の得点の合計はBチームの全試合の得点の合計より多い。
㋑Aチームの得点の最頻値はAチームの得点の平均値と等しいが、Bチームの得点の最頻値はBチームの得点の平均値と異なる。
㋒Aチームの得点の範囲はBチームの得点の範囲より大きく、Aチームが10点以上得点した試合数はBチームが10点以上得点した試合数より多い。
㋓Aチームの得点の平均値はBチームの得点の平均値より大きく、Aチームの得点の最頻値はBチームの得点の最頻値より小さい。
㋔Aチームの得点は、Aチームの試合の半数以上でAチームの得点の平均値以上である。
※図/表は動画内参照
この動画を見る
◎ある年の7月に、野球チームA、Bがそれぞれ試合を行った。
右の図は、Aチームが行った全試合におけるそれぞれの得点の記録をヒストグラムに表したものである。
また、表は、Bチームが行った全試合におけるそれぞれの得点の記録を度数分布表にまとめたものであり、Bチームが行った全試合の得点の合計は108点である。
このとき、①~③に答えよう。
①図における中央値を求めよう。
②表の中の(i),(ii)にあてはまる数を求めよう。
③図、表からわかることとして正しいものを次の㋐~㋔の中から2つ選ぼう。
㋐Aチームの試合数はBチームの試合数より多く、Aチームの全試合の得点の合計はBチームの全試合の得点の合計より多い。
㋑Aチームの得点の最頻値はAチームの得点の平均値と等しいが、Bチームの得点の最頻値はBチームの得点の平均値と異なる。
㋒Aチームの得点の範囲はBチームの得点の範囲より大きく、Aチームが10点以上得点した試合数はBチームが10点以上得点した試合数より多い。
㋓Aチームの得点の平均値はBチームの得点の平均値より大きく、Aチームの得点の最頻値はBチームの得点の最頻値より小さい。
㋔Aチームの得点は、Aチームの試合の半数以上でAチームの得点の平均値以上である。
※図/表は動画内参照
【受験対策】数学-資料の活用②

単元:
#数学(中学生)#中1数学#資料の活用
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎生徒数40人のクラスで、1ヶ月間に1人1人が読んだ本の冊数を調べた。
図Aは、その結果をヒストグラムに表したものである。
このとき、次の①、②に答えよう。
①読んだ本の冊数が8冊以上の生徒は、クラス全体の何%か、求めよう。
②読んだ本の冊数の中央値を求めよう。
③図Bは、あるクラスの生徒20人が冬休み中に読んだ本の冊数を、ヒストグラムに表したものである。
この20人が読んだ本の冊数について述べた文として適切なものを、次の㋐~㋓のうちから1つ選ぼう。
㋐分布の範囲(レンジ)は、4冊である。
㋑最頻値(モード)は、5冊である。
㋒中央値(メジアン)は、3冊である。
㋓平均値は、2.3冊である。
※図は動画内参照
この動画を見る
◎生徒数40人のクラスで、1ヶ月間に1人1人が読んだ本の冊数を調べた。
図Aは、その結果をヒストグラムに表したものである。
このとき、次の①、②に答えよう。
①読んだ本の冊数が8冊以上の生徒は、クラス全体の何%か、求めよう。
②読んだ本の冊数の中央値を求めよう。
③図Bは、あるクラスの生徒20人が冬休み中に読んだ本の冊数を、ヒストグラムに表したものである。
この20人が読んだ本の冊数について述べた文として適切なものを、次の㋐~㋓のうちから1つ選ぼう。
㋐分布の範囲(レンジ)は、4冊である。
㋑最頻値(モード)は、5冊である。
㋒中央値(メジアン)は、3冊である。
㋓平均値は、2.3冊である。
※図は動画内参照
【受験対策】数学-資料の活用①

単元:
#数学(中学生)#中1数学#資料の活用
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①資料Aは、ある中学校の3年生男子11名が行った反復横跳びの回数を記録したものである。
中央値を求めよう。
②表Bは、あるサッカーチームが行った試合の得点の記録をまとめたものである。この表から試合の得点の最頻値と平均値を求めよう。
③表Cは、あるクラスの生徒33人に対して50m走を実施し、その記録を度数分布表 にまとめたものである。度数が最も多い階級の階級値を求めよう。
※資料/表は動画内参照
この動画を見る
①資料Aは、ある中学校の3年生男子11名が行った反復横跳びの回数を記録したものである。
中央値を求めよう。
②表Bは、あるサッカーチームが行った試合の得点の記録をまとめたものである。この表から試合の得点の最頻値と平均値を求めよう。
③表Cは、あるクラスの生徒33人に対して50m走を実施し、その記録を度数分布表 にまとめたものである。度数が最も多い階級の階級値を求めよう。
※資料/表は動画内参照
【受験対策】 数学-小問①

単元:
#数学(中学生)#中2数学#中3数学#方程式#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎次の計算をしよう。
①$-5-8 \times \displaystyle \frac{1}{4}$
②$-3+5 \times (-1)^3$
③$4(2x-y)-3(x+y)$
④$\displaystyle \frac{1}{2}(3a-2b)-(2a-b)$
⑤一次方程式$x-7=9(x+1)$を解こう。
⑥等式$2a-3b=1$を$b$について解こう。
⑦等式$a=\displaystyle \frac{b+c}{2}$をcについて解こう。
この動画を見る
◎次の計算をしよう。
①$-5-8 \times \displaystyle \frac{1}{4}$
②$-3+5 \times (-1)^3$
③$4(2x-y)-3(x+y)$
④$\displaystyle \frac{1}{2}(3a-2b)-(2a-b)$
⑤一次方程式$x-7=9(x+1)$を解こう。
⑥等式$2a-3b=1$を$b$について解こう。
⑦等式$a=\displaystyle \frac{b+c}{2}$をcについて解こう。
中学数学(方程式・高校入試対策)【篠原好】

【受験対策】 数学-図形③
単元:
#数学(中学生)#中1数学#中3数学#相似な図形#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
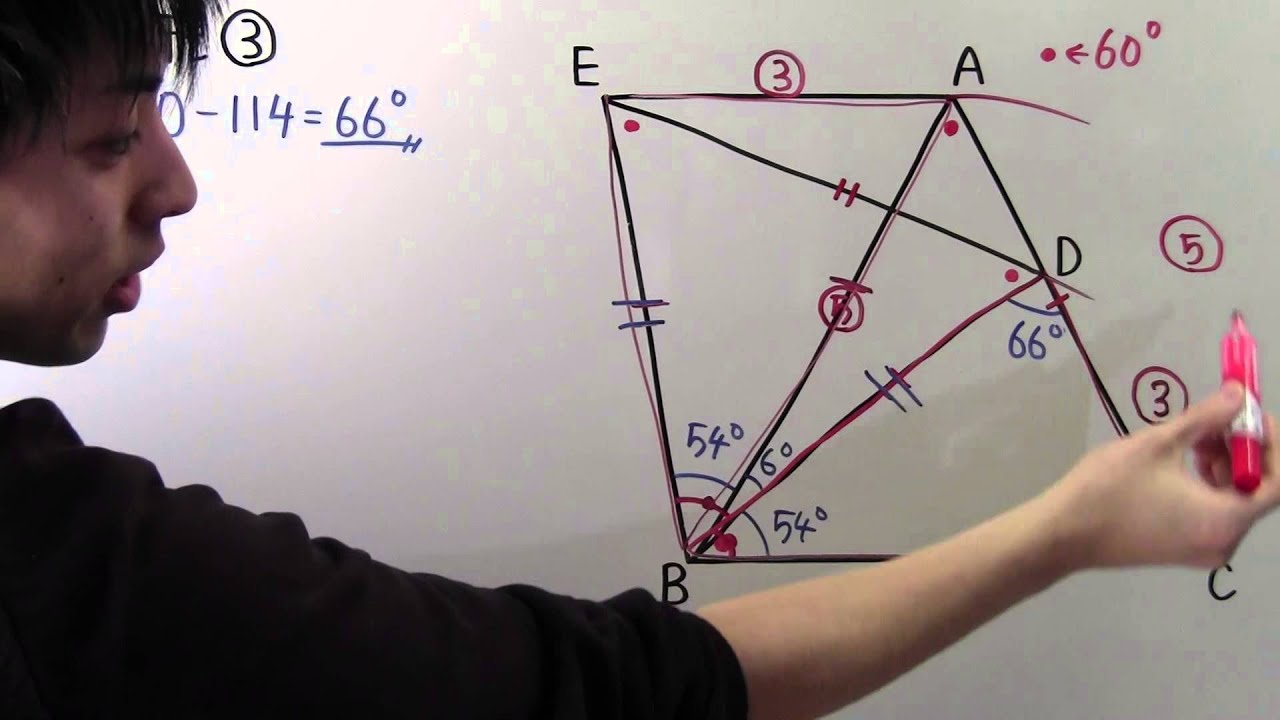
右の図で、△ABC,△BDEはどちらも正三角形で辺AC上に頂点Dがあります。
AB:AE=5:3のとき、次の問いに答えよう。
①$\angle ABE=54°$のとき、$\angle BDC$の大きさは?
②AD:CDを、最も簡単な整数の比で求めよう。
③△ABDの面積は四角形EBCAの面積の何倍?
※図は動画内参照
この動画を見る
右の図で、△ABC,△BDEはどちらも正三角形で辺AC上に頂点Dがあります。
AB:AE=5:3のとき、次の問いに答えよう。
①$\angle ABE=54°$のとき、$\angle BDC$の大きさは?
②AD:CDを、最も簡単な整数の比で求めよう。
③△ABDの面積は四角形EBCAの面積の何倍?
※図は動画内参照
【受験対策】 数学-図形②
単元:
#数学(中学生)#中1数学#中3数学#相似な図形#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①右の[図1]のような図形を組み立てて、三角柱の形をした容器をつくりました。
この容器を立てて、中に48$cm^3$の水を入れたとき、水が容器にふれている部分の面積を 求めよう。
ただし、容器の厚みは考えないものとし、水がこぼれることもないものとします。
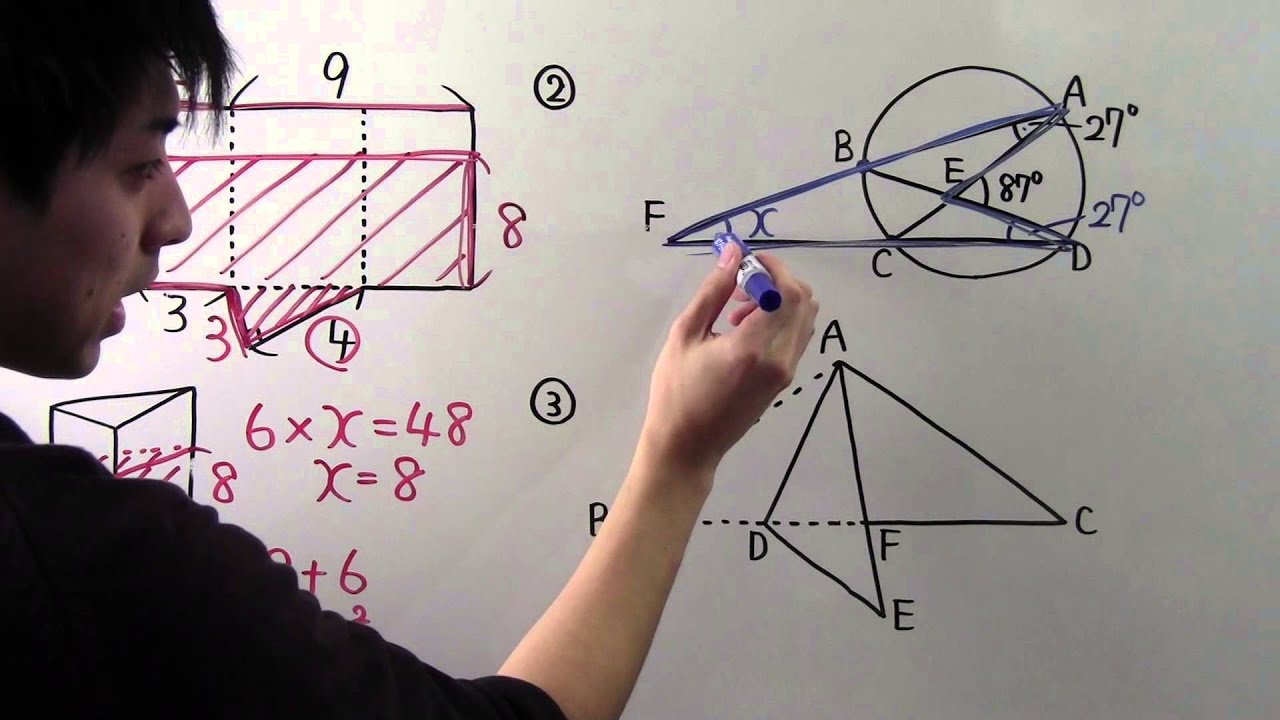
② 右の[図2]のように、円周上に点A、B、C、Dがあります。
ACとBDの交点をEとし、直線ABと直線CDの交点をF とします。
$\angle BAC=27°\angle AED=87°$のとき、 $\angle AFD$の大きさを求めよう。
③右の[図3]で、△ABCはAB=ACの二等辺三角形です。
辺BC上に点Dをとり、ADを折り目として折り返し、
頂点Bが移った位置をEとします。
辺BCとAEの交点をFと すると、FD=FEになりました。
$\angle BAD=42°$のとき、 $\angle ACB$の大きさを求めよう。
※図は動画内参照
この動画を見る
①右の[図1]のような図形を組み立てて、三角柱の形をした容器をつくりました。
この容器を立てて、中に48$cm^3$の水を入れたとき、水が容器にふれている部分の面積を 求めよう。
ただし、容器の厚みは考えないものとし、水がこぼれることもないものとします。
② 右の[図2]のように、円周上に点A、B、C、Dがあります。
ACとBDの交点をEとし、直線ABと直線CDの交点をF とします。
$\angle BAC=27°\angle AED=87°$のとき、 $\angle AFD$の大きさを求めよう。
③右の[図3]で、△ABCはAB=ACの二等辺三角形です。
辺BC上に点Dをとり、ADを折り目として折り返し、
頂点Bが移った位置をEとします。
辺BCとAEの交点をFと すると、FD=FEになりました。
$\angle BAD=42°$のとき、 $\angle ACB$の大きさを求めよう。
※図は動画内参照
【受験対策】 数学-関数④
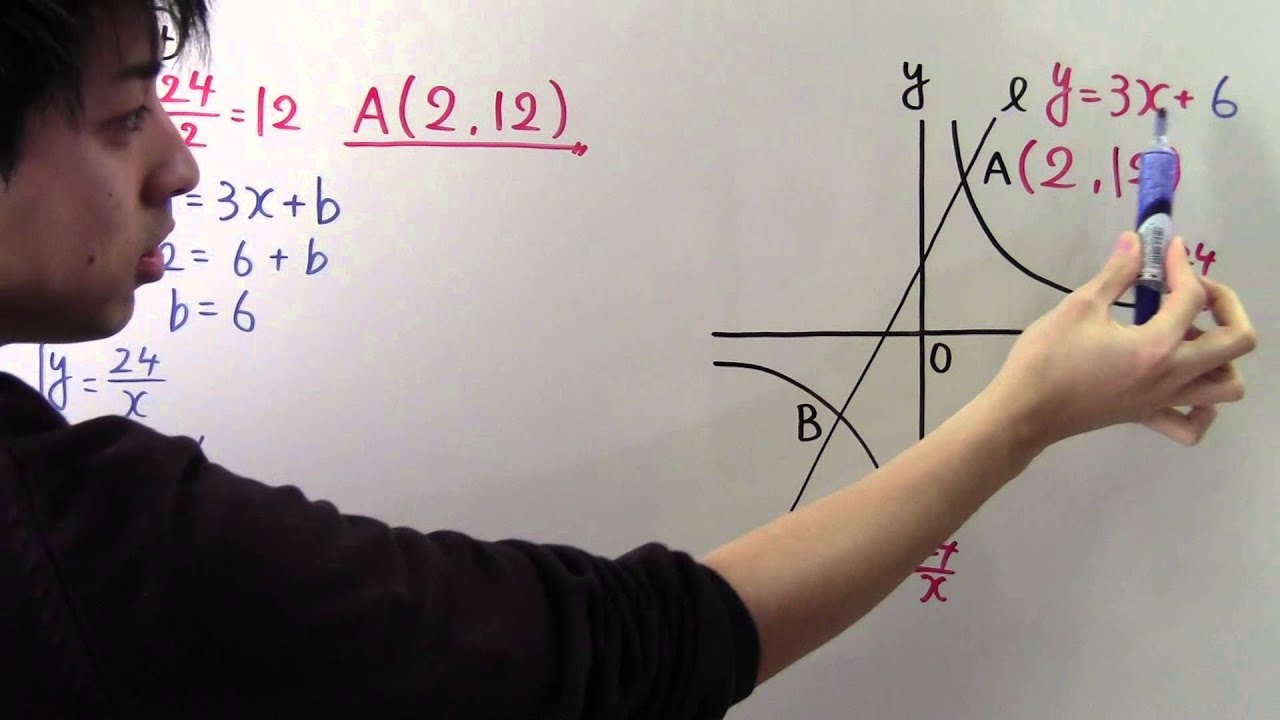
単元:
#数学(中学生)#中1数学#中2数学#比例・反比例#1次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右の図のように、関数$y=\displaystyle \frac{24}{x}$とそのグラフ上の点Aがある。
直線又は点Aを通る傾きが3の直線で、 関数$y=\displaystyle \frac{24}{x}$とのもう一つの交点をBとします。
点Aのx座標が2のとき、次の問いに答えよう。
①点Aの座標は?
②点Bの座標は?
③△OABの面積は?
※図は動画内参照
この動画を見る
右の図のように、関数$y=\displaystyle \frac{24}{x}$とそのグラフ上の点Aがある。
直線又は点Aを通る傾きが3の直線で、 関数$y=\displaystyle \frac{24}{x}$とのもう一つの交点をBとします。
点Aのx座標が2のとき、次の問いに答えよう。
①点Aの座標は?
②点Bの座標は?
③△OABの面積は?
※図は動画内参照
【中1 数学】中1-78 おうぎ形の弧と面積④ ~さらにややこしい図形編~

単元:
#数学(中学生)#中1数学#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎色のついている部分の面積と周の長さをもとめよう!
①
[面]
[周]
②
ACを直径とする半径は、ABを直径とする
半円を点Aを中心に30°回転させたもの。
[面]
[周]
※図は動画内参照
この動画を見る
◎色のついている部分の面積と周の長さをもとめよう!
①
[面]
[周]
②
ACを直径とする半径は、ABを直径とする
半円を点Aを中心に30°回転させたもの。
[面]
[周]
※図は動画内参照
【中1 数学】中1-77 おうぎ形の弧と面積③ ~ややこしい図形編~

単元:
#数学(中学生)#中1数学#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎色のついている部分の面積と周の長さをもとめよう!
①
[面]
[周]
②
[面]
[周]
※図は動画内参照
この動画を見る
◎色のついている部分の面積と周の長さをもとめよう!
①
[面]
[周]
②
[面]
[周]
※図は動画内参照
(撮り直し前)【中1 数学】 中1-76 おうぎ形の弧と面積② ・ 応用編

単元:
#数学(中学生)#中1数学#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①半径9cm、面積36π$cm^2$のおうぎ形の中心角の大きさと弧の長さをもとめよう!
②半径6cm、弧の長さ9πcmのおうぎ形の中心角の大きさと面積をもとめよう!
この動画を見る
①半径9cm、面積36π$cm^2$のおうぎ形の中心角の大きさと弧の長さをもとめよう!
②半径6cm、弧の長さ9πcmのおうぎ形の中心角の大きさと面積をもとめよう!
【中1 数学】中1-75 おうぎ形の弧と面積① ~基本編~

単元:
#数学(中学生)#中1数学#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
[円]
面積=①________
円周=②________
[おうぎ形]
面積=③________
弧=④________
◎半径12cm、中心角60°のおうぎ形について。
⑤面積は?
⑥弧の長さは?
◎半径5cm、中心角144°のおうぎ形について。
⑦面積は?
⑧弧の長さは?
この動画を見る
[円]
面積=①________
円周=②________
[おうぎ形]
面積=③________
弧=④________
◎半径12cm、中心角60°のおうぎ形について。
⑤面積は?
⑥弧の長さは?
◎半径5cm、中心角144°のおうぎ形について。
⑦面積は?
⑧弧の長さは?
【中1 数学】中1-74 円とおうぎ形の性質③ ~おうぎ形編~
単元:
#数学(中学生)#中1数学#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
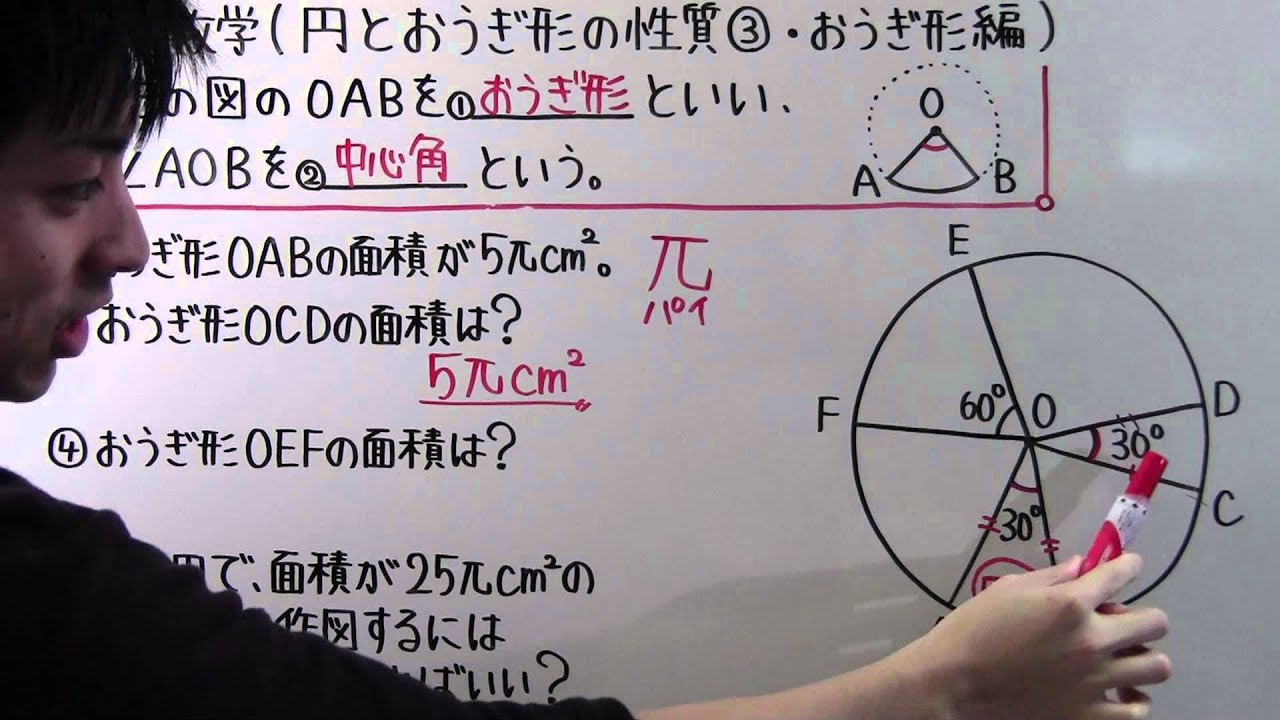
右の図のOABを①____といい、
$\angle AOB$を②____という。
◎おうぎ形OABの面積が$5πcm^2$。
③おうぎ形OCDの面積は?
④おうぎ形OEFの面積は?
⑤右の円で、面積が$25πcm^2$のおうぎ形を作図するには
中心角を何度にすればいい?
※図は動画内参照
この動画を見る
右の図のOABを①____といい、
$\angle AOB$を②____という。
◎おうぎ形OABの面積が$5πcm^2$。
③おうぎ形OCDの面積は?
④おうぎ形OEFの面積は?
⑤右の円で、面積が$25πcm^2$のおうぎ形を作図するには
中心角を何度にすればいい?
※図は動画内参照
【中1 数学】中1-73 円とおうぎ形の性質② ~作図編~

単元:
#数学(中学生)#中1数学#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①点Aが接点となるように接線ℓを作図しよう!
②中心が直線m上にあって点Aで直線ℓに接する円を作図しよう!
③割れた円形の皿の中心Oを作図しよう!
④点Aで直線OYに接して、かつ直線OXにも接する円を作図しよう!
※図は動画内参照
この動画を見る
①点Aが接点となるように接線ℓを作図しよう!
②中心が直線m上にあって点Aで直線ℓに接する円を作図しよう!
③割れた円形の皿の中心Oを作図しよう!
④点Aで直線OYに接して、かつ直線OXにも接する円を作図しよう!
※図は動画内参照
