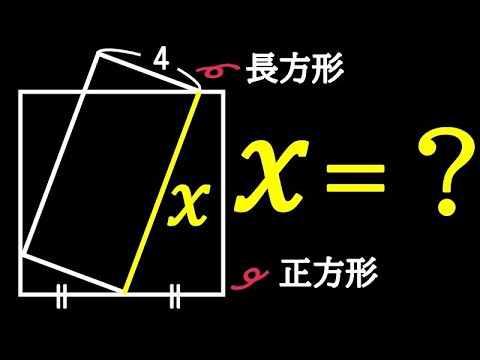
問題文全文(内容文):
~例題~
次の図の$\triangle ABC$で,点$D,E$は辺$AB$上の点で点$F,G$は辺$BC$上の点です.
線分$EF,DF,DG,AG$によって,$\triangle ABC$の面積が5等分されています.
(1)
$BG:GC$を最も簡単な整数の比で表しなさい.
(2)
$BC=15$cmのとき,$BF$の長さを求めなさい.
~例題~
次の図の$\triangle ABC$で,点$D,E$は辺$AB$上の点で点$F,G$は辺$BC$上の点です.
線分$EF,DF,DG,AG$によって,$\triangle ABC$の面積が5等分されています.
(1)
$BG:GC$を最も簡単な整数の比で表しなさい.
(2)
$BC=15$cmのとき,$BF$の長さを求めなさい.
単元:
#数学(中学生)#中2数学#三角形と四角形
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
~例題~
次の図の$\triangle ABC$で,点$D,E$は辺$AB$上の点で点$F,G$は辺$BC$上の点です.
線分$EF,DF,DG,AG$によって,$\triangle ABC$の面積が5等分されています.
(1)
$BG:GC$を最も簡単な整数の比で表しなさい.
(2)
$BC=15$cmのとき,$BF$の長さを求めなさい.
~例題~
次の図の$\triangle ABC$で,点$D,E$は辺$AB$上の点で点$F,G$は辺$BC$上の点です.
線分$EF,DF,DG,AG$によって,$\triangle ABC$の面積が5等分されています.
(1)
$BG:GC$を最も簡単な整数の比で表しなさい.
(2)
$BC=15$cmのとき,$BF$の長さを求めなさい.
投稿日:2023.04.27