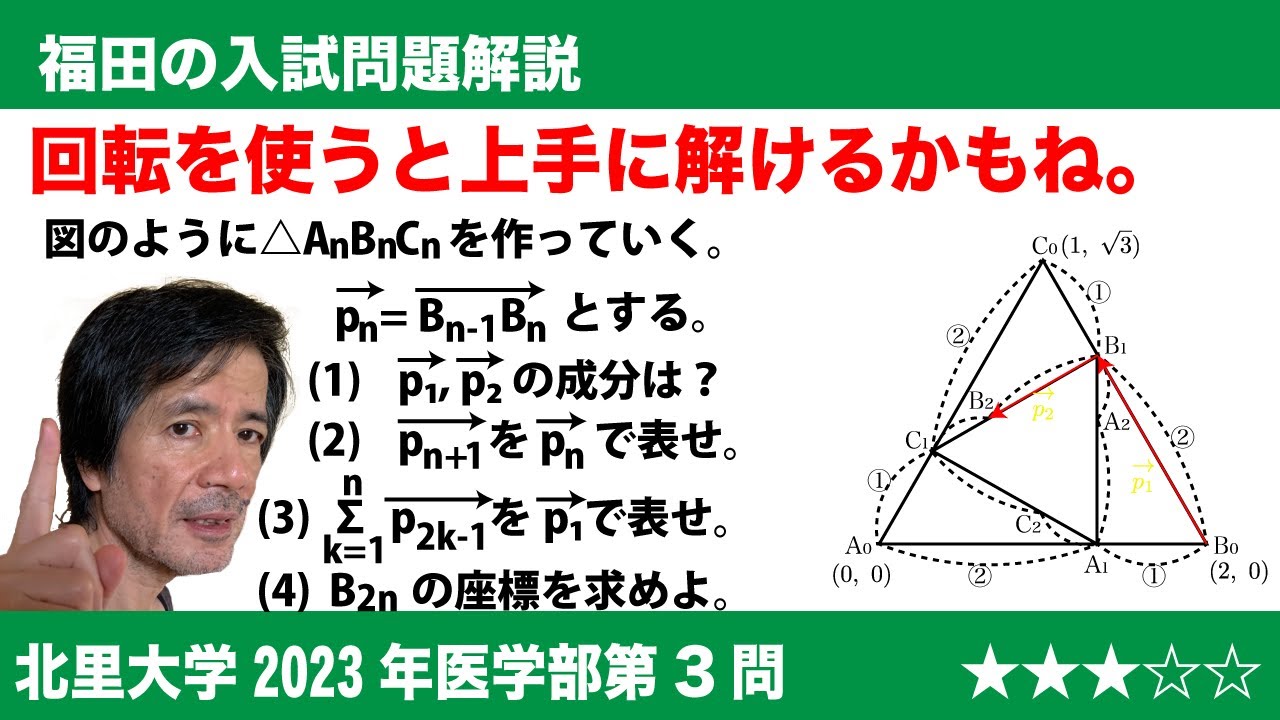
問題文全文(内容文):
平面上に3点$O,P_{1},P_{2}$が、$|\overrightarrow{OP_{1}}|=\sqrt{6}$,$|\overrightarrow{OP_{2}}|=\dfrac{\sqrt{30}}{5}$,$\overrightarrow{OP_{1}}\bot\overrightarrow{OP_{2}}$となるように与えられている。また、点Oから直線$P_{1}P_{2}$との交点をHとする。さらに平面上に点$P_{3},P_{4},P_{5}$,・・・を、n=1,2,3,・・・に対し、点$P_{n+2}$が点$P_{n}$tと$点P_{n+1}$を結ぶ線分$P_{n}P_{n+1}$を4:1に内分するように定める。
(1)$\overrightarrow{OP_{1}}$と$\overrightarrow{OP_{2}}$を使って、$\overrightarrow{OH}$を表すと$\overrightarrow{OH}=\fbox{(ア)}$である。
(2)$\overrightarrow{P_{1}P_{2}}$を使って、$\overrightarrow{HP_{n}}$をnを用いた式で表すと$\overrightarrow{HP_{n}}=\fbox{(イ)}$である。
(3)ベクトルを使わずに、$\overrightarrow{|OP_{n}|^2}$をnを用いた式で表すと$\overrightarrow{|OP_{n}|^2}$である。
2023慶應義塾大学商学部過去問
平面上に3点$O,P_{1},P_{2}$が、$|\overrightarrow{OP_{1}}|=\sqrt{6}$,$|\overrightarrow{OP_{2}}|=\dfrac{\sqrt{30}}{5}$,$\overrightarrow{OP_{1}}\bot\overrightarrow{OP_{2}}$となるように与えられている。また、点Oから直線$P_{1}P_{2}$との交点をHとする。さらに平面上に点$P_{3},P_{4},P_{5}$,・・・を、n=1,2,3,・・・に対し、点$P_{n+2}$が点$P_{n}$tと$点P_{n+1}$を結ぶ線分$P_{n}P_{n+1}$を4:1に内分するように定める。
(1)$\overrightarrow{OP_{1}}$と$\overrightarrow{OP_{2}}$を使って、$\overrightarrow{OH}$を表すと$\overrightarrow{OH}=\fbox{(ア)}$である。
(2)$\overrightarrow{P_{1}P_{2}}$を使って、$\overrightarrow{HP_{n}}$をnを用いた式で表すと$\overrightarrow{HP_{n}}=\fbox{(イ)}$である。
(3)ベクトルを使わずに、$\overrightarrow{|OP_{n}|^2}$をnを用いた式で表すと$\overrightarrow{|OP_{n}|^2}$である。
2023慶應義塾大学商学部過去問
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
平面上に3点$O,P_{1},P_{2}$が、$|\overrightarrow{OP_{1}}|=\sqrt{6}$,$|\overrightarrow{OP_{2}}|=\dfrac{\sqrt{30}}{5}$,$\overrightarrow{OP_{1}}\bot\overrightarrow{OP_{2}}$となるように与えられている。また、点Oから直線$P_{1}P_{2}$との交点をHとする。さらに平面上に点$P_{3},P_{4},P_{5}$,・・・を、n=1,2,3,・・・に対し、点$P_{n+2}$が点$P_{n}$tと$点P_{n+1}$を結ぶ線分$P_{n}P_{n+1}$を4:1に内分するように定める。
(1)$\overrightarrow{OP_{1}}$と$\overrightarrow{OP_{2}}$を使って、$\overrightarrow{OH}$を表すと$\overrightarrow{OH}=\fbox{(ア)}$である。
(2)$\overrightarrow{P_{1}P_{2}}$を使って、$\overrightarrow{HP_{n}}$をnを用いた式で表すと$\overrightarrow{HP_{n}}=\fbox{(イ)}$である。
(3)ベクトルを使わずに、$\overrightarrow{|OP_{n}|^2}$をnを用いた式で表すと$\overrightarrow{|OP_{n}|^2}$である。
2023慶應義塾大学商学部過去問
平面上に3点$O,P_{1},P_{2}$が、$|\overrightarrow{OP_{1}}|=\sqrt{6}$,$|\overrightarrow{OP_{2}}|=\dfrac{\sqrt{30}}{5}$,$\overrightarrow{OP_{1}}\bot\overrightarrow{OP_{2}}$となるように与えられている。また、点Oから直線$P_{1}P_{2}$との交点をHとする。さらに平面上に点$P_{3},P_{4},P_{5}$,・・・を、n=1,2,3,・・・に対し、点$P_{n+2}$が点$P_{n}$tと$点P_{n+1}$を結ぶ線分$P_{n}P_{n+1}$を4:1に内分するように定める。
(1)$\overrightarrow{OP_{1}}$と$\overrightarrow{OP_{2}}$を使って、$\overrightarrow{OH}$を表すと$\overrightarrow{OH}=\fbox{(ア)}$である。
(2)$\overrightarrow{P_{1}P_{2}}$を使って、$\overrightarrow{HP_{n}}$をnを用いた式で表すと$\overrightarrow{HP_{n}}=\fbox{(イ)}$である。
(3)ベクトルを使わずに、$\overrightarrow{|OP_{n}|^2}$をnを用いた式で表すと$\overrightarrow{|OP_{n}|^2}$である。
2023慶應義塾大学商学部過去問
投稿日:2023.11.28