問題文全文(内容文):
${\Large\boxed{2}}$
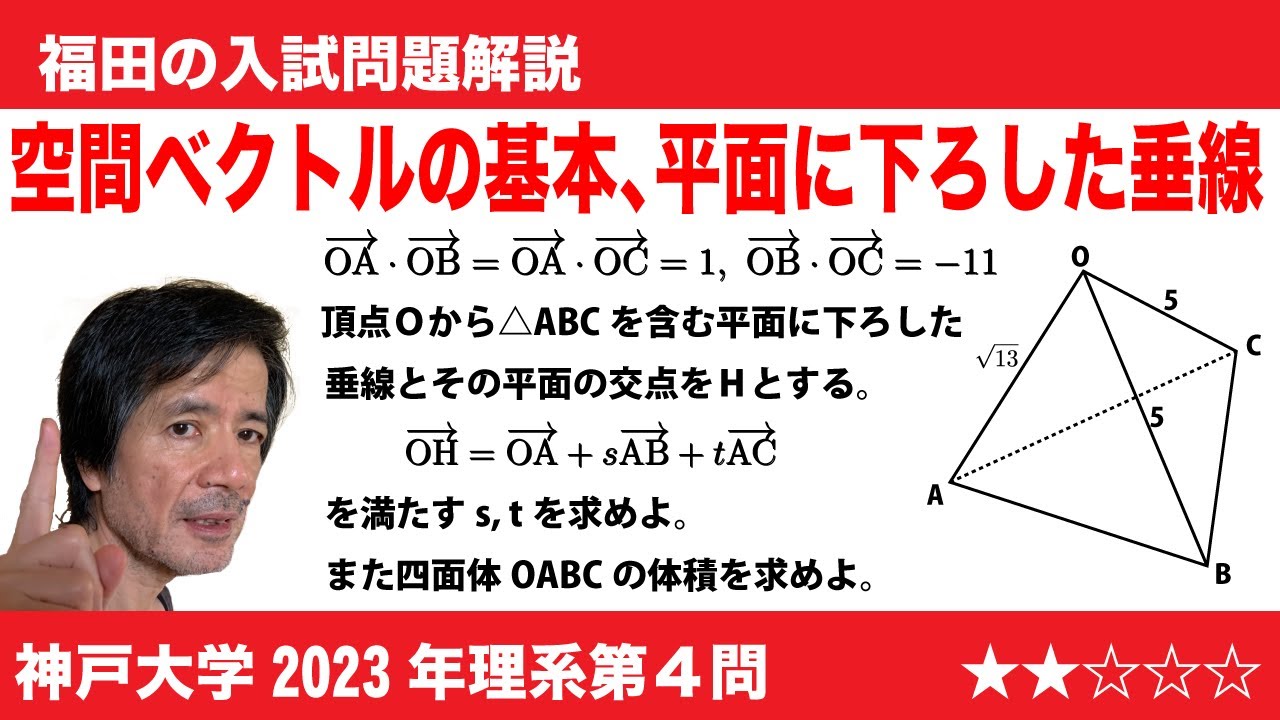
図(※動画参照)のように、1辺の長さが$2$である立方体$\rm ABCD-EFGH$の内側に、正方形$\rm ABCD$に内接する円を底面にもつ高さ$2$の円柱$V$をとる。次の設問に答えよ。
(1)立方体の対角線$\rm AG$と円柱$V$の共通部分と得られる線分の長さを求めよ。
(2)$W$を三角柱$\rm ABC-DCG$と三角柱$\rm AEH-BFG$の共通部分とする。円柱$V$の側面と$W$の共通部分に含まれる線分の長さの最大値を求めよ。
2021早稲田大学商学部過去問
${\Large\boxed{2}}$
図(※動画参照)のように、1辺の長さが$2$である立方体$\rm ABCD-EFGH$の内側に、正方形$\rm ABCD$に内接する円を底面にもつ高さ$2$の円柱$V$をとる。次の設問に答えよ。
(1)立方体の対角線$\rm AG$と円柱$V$の共通部分と得られる線分の長さを求めよ。
(2)$W$を三角柱$\rm ABC-DCG$と三角柱$\rm AEH-BFG$の共通部分とする。円柱$V$の側面と$W$の共通部分に含まれる線分の長さの最大値を求めよ。
2021早稲田大学商学部過去問
単元:
#数A#大学入試過去問(数学)#図形の性質#学校別大学入試過去問解説(数学)#空間における垂直と平行と多面体(オイラーの法則)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$
図(※動画参照)のように、1辺の長さが$2$である立方体$\rm ABCD-EFGH$の内側に、正方形$\rm ABCD$に内接する円を底面にもつ高さ$2$の円柱$V$をとる。次の設問に答えよ。
(1)立方体の対角線$\rm AG$と円柱$V$の共通部分と得られる線分の長さを求めよ。
(2)$W$を三角柱$\rm ABC-DCG$と三角柱$\rm AEH-BFG$の共通部分とする。円柱$V$の側面と$W$の共通部分に含まれる線分の長さの最大値を求めよ。
2021早稲田大学商学部過去問
${\Large\boxed{2}}$
図(※動画参照)のように、1辺の長さが$2$である立方体$\rm ABCD-EFGH$の内側に、正方形$\rm ABCD$に内接する円を底面にもつ高さ$2$の円柱$V$をとる。次の設問に答えよ。
(1)立方体の対角線$\rm AG$と円柱$V$の共通部分と得られる線分の長さを求めよ。
(2)$W$を三角柱$\rm ABC-DCG$と三角柱$\rm AEH-BFG$の共通部分とする。円柱$V$の側面と$W$の共通部分に含まれる線分の長さの最大値を求めよ。
2021早稲田大学商学部過去問
投稿日:2021.06.12