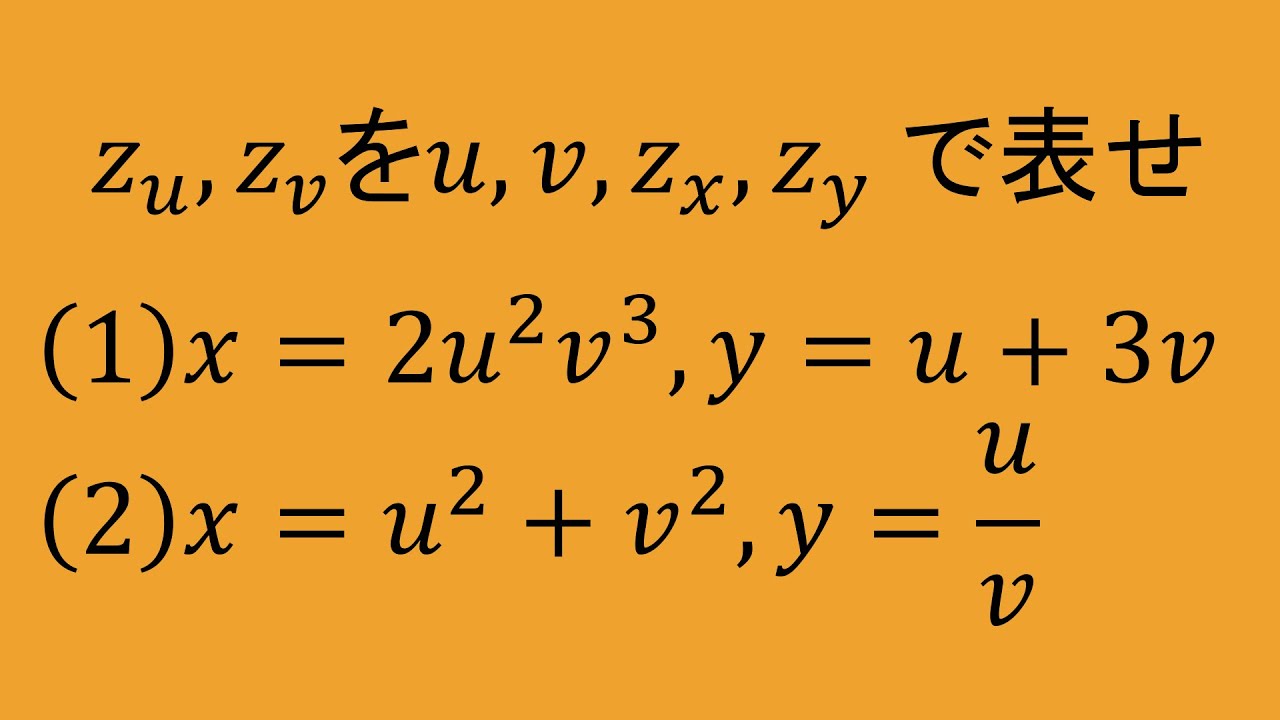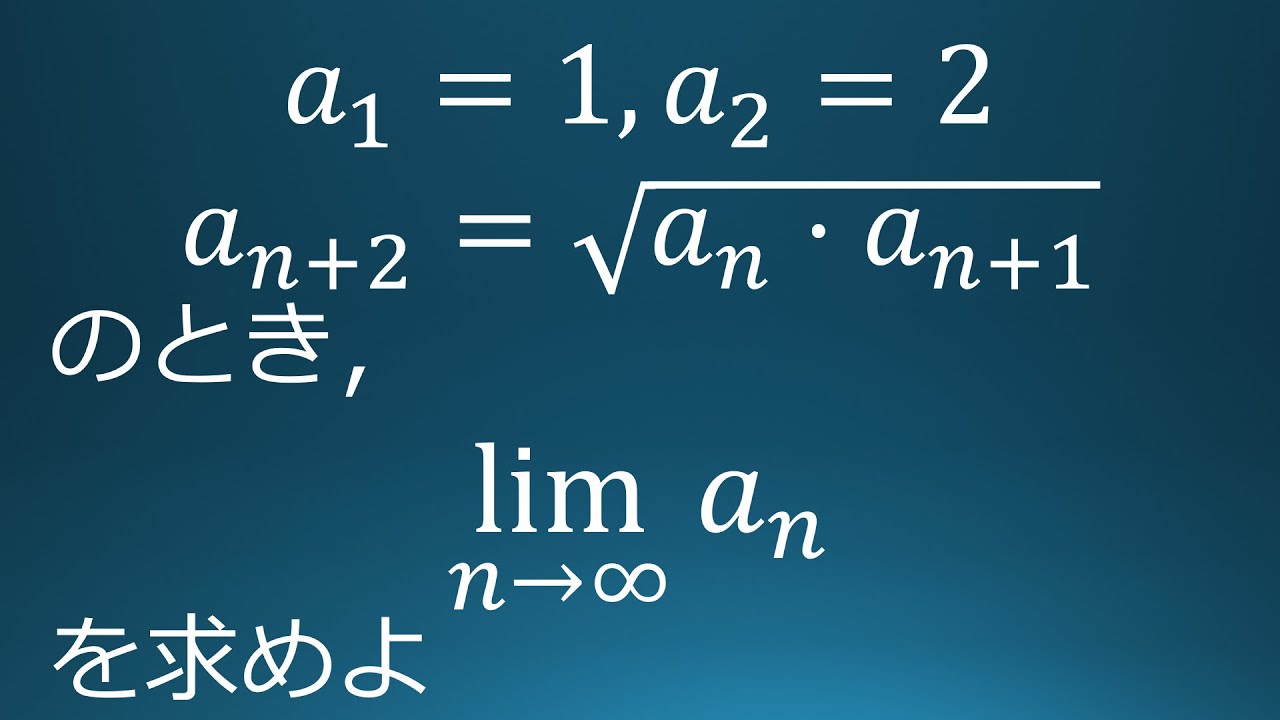問題文全文(内容文):
$e=\displaystyle\lim_{n \to \infty}(1+\frac{1}{n})^n$
$\displaystyle\lim_{n \to -\infty}(1+\frac{1}{n})^n=e$を示せ
$e=\displaystyle\lim_{n \to \infty}(1+\frac{1}{n})^n$
$\displaystyle\lim_{n \to -\infty}(1+\frac{1}{n})^n=e$を示せ
単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$e=\displaystyle\lim_{n \to \infty}(1+\frac{1}{n})^n$
$\displaystyle\lim_{n \to -\infty}(1+\frac{1}{n})^n=e$を示せ
$e=\displaystyle\lim_{n \to \infty}(1+\frac{1}{n})^n$
$\displaystyle\lim_{n \to -\infty}(1+\frac{1}{n})^n=e$を示せ
投稿日:2023.06.18