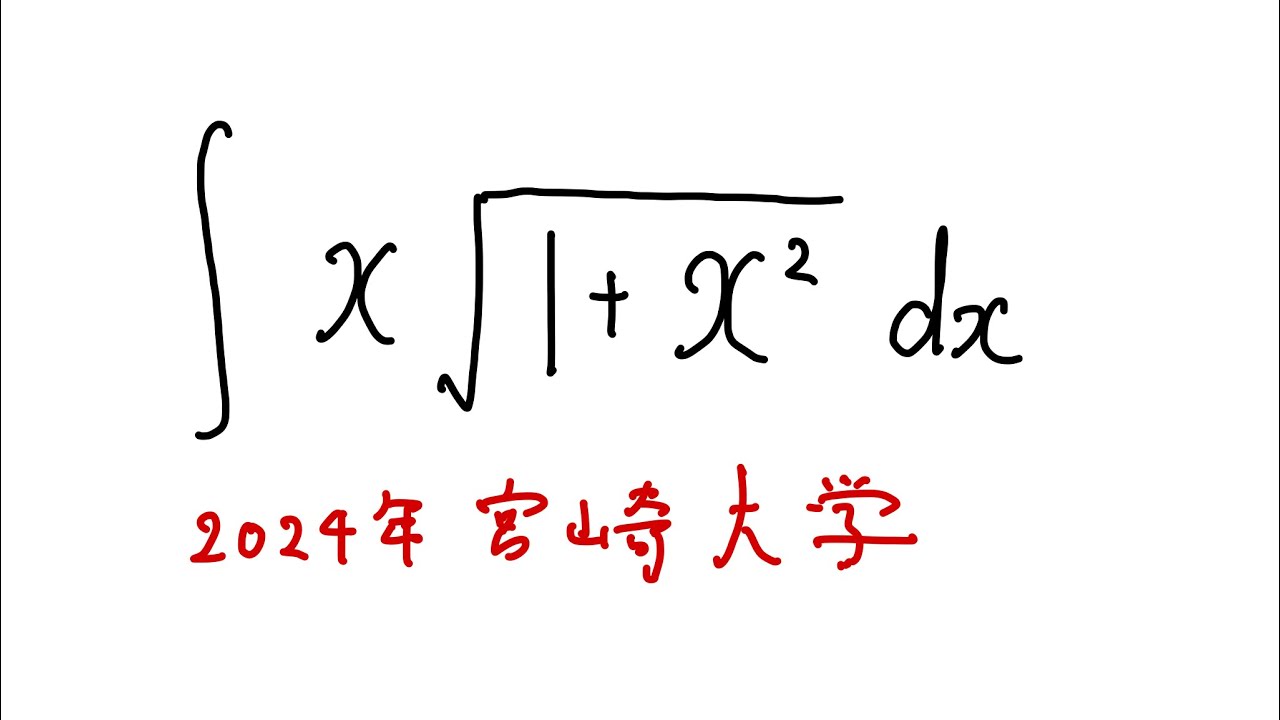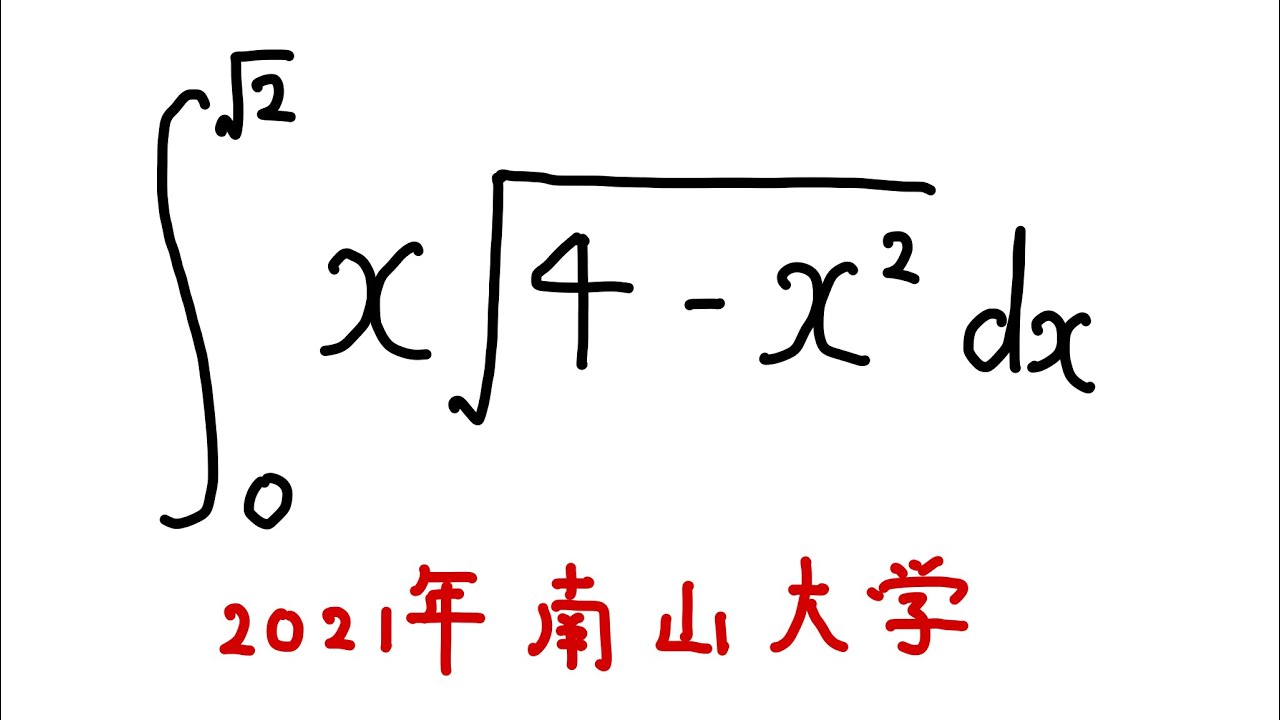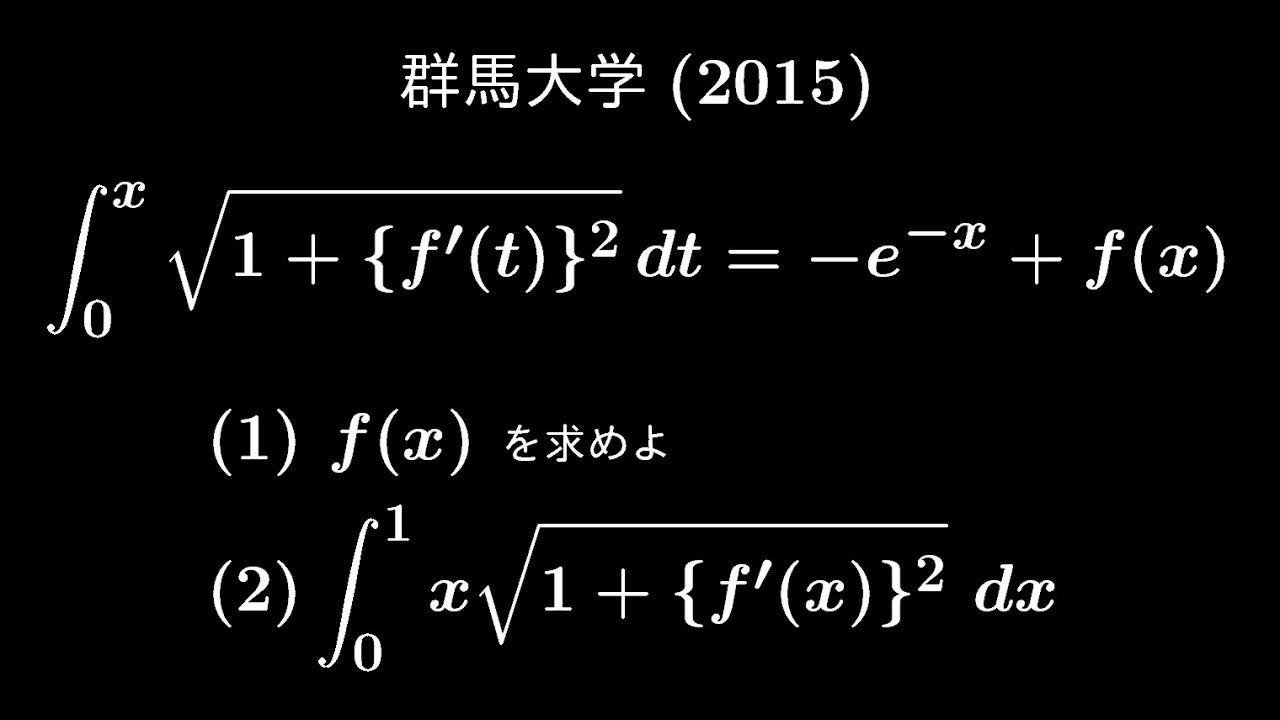【数Ⅲ】積分で体積を求める【細かくちぎって足し合わせる、積分の原理】 - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(高校生) > 数Ⅲ > 積分とその応用 > 面積・体積・長さ・速度 > 【数Ⅲ】積分で体積を求める【細かくちぎって足し合わせる、積分の原理】

【数Ⅲ】積分で体積を求める【細かくちぎって足し合わせる、積分の原理】

問題文全文(内容文)：
(1)$ y=\sin x(0 \leqq x \leqq \pi)$上の点Pからx軸に下ろした垂線の足を点Qとする.
PQを1辺とするxy平面に垂直な正方形を作る.点Pが(0,0)から$ (\pi,0)$まで動くとき,
この正方形が通過する部分の体積を求めよ.
(2)$ y=x^2-3x $とx軸で囲まれた部分をx軸の周りに1回転させてできる立体の体積を求めよ.
単元： #積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師： めいちゃんねる
問題文全文(内容文)：
(1)$ y=\sin x(0 \leqq x \leqq \pi)$上の点Pからx軸に下ろした垂線の足を点Qとする.
PQを1辺とするxy平面に垂直な正方形を作る.点Pが(0,0)から$ (\pi,0)$まで動くとき,
この正方形が通過する部分の体積を求めよ.
(2)$ y=x^2-3x $とx軸で囲まれた部分をx軸の周りに1回転させてできる立体の体積を求めよ.
投稿日：2023.05.13

＜関連動画＞

大学入試問題#134　京都工芸繊維大学(2018)　不定積分

アイキャッチ画像
単元： #積分とその応用#不定積分#数学(高校生)#数Ⅲ
指導講師： ますただ
問題文全文(内容文)：
$\displaystyle \int \{log(3+\cos^2\theta)\}\cos\theta d \theta$を計算せよ。

出典：2018年京都工芸繊維大学　入試問題
この動画を見る　

【数Ⅲ】積分法：②バウムクーヘン型積分！　曲線y=e^x,x=1,x軸,y軸によって囲まれた部分をy軸の周りに1回転させてできる立体の体積を求めよ

アイキャッチ画像
単元： #積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師： 理数個別チャンネル
問題文全文(内容文)：
曲線$y=e^x,x=1$,x軸,y軸によって囲まれた部分をy軸の周りに1回転させてできる立体の体積を求めよ
この動画を見る　

2024年6月28日

アイキャッチ画像
単元： #大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#九州歯科大学
指導講師： ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1} \displaystyle \frac{1}{1+e^x}$ $dx$

出典：2023年九州歯科大学
この動画を見る　

右左どっちでできた問題がヤバい...

アイキャッチ画像
単元： #積分とその応用#不定積分#数学(高校生)#数Ⅲ
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
次の不定積分を求めよ
$\displaystyle
\begin{eqnarray}
\int \frac{\sin{\frac{1}{x}}}{x^3} dx
\end{eqnarray}
$
この動画を見る　

大学入試問題#462「~らん~さんからの紹介」　横国・信州大学　類題　#定積分

アイキャッチ画像
単元： #大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#信州大学#数Ⅲ
指導講師： ますただ
問題文全文(内容文)：
$\displaystyle \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \displaystyle \frac{e^x+e^{-x}}{e^{(\sin^5x+1)}+e} dx$
この動画を見る　
Back to top