正多角形と円との関係は、スイカと塩の関係のようなものだ。花巻東（岩手県）

問題文全文(内容文)：
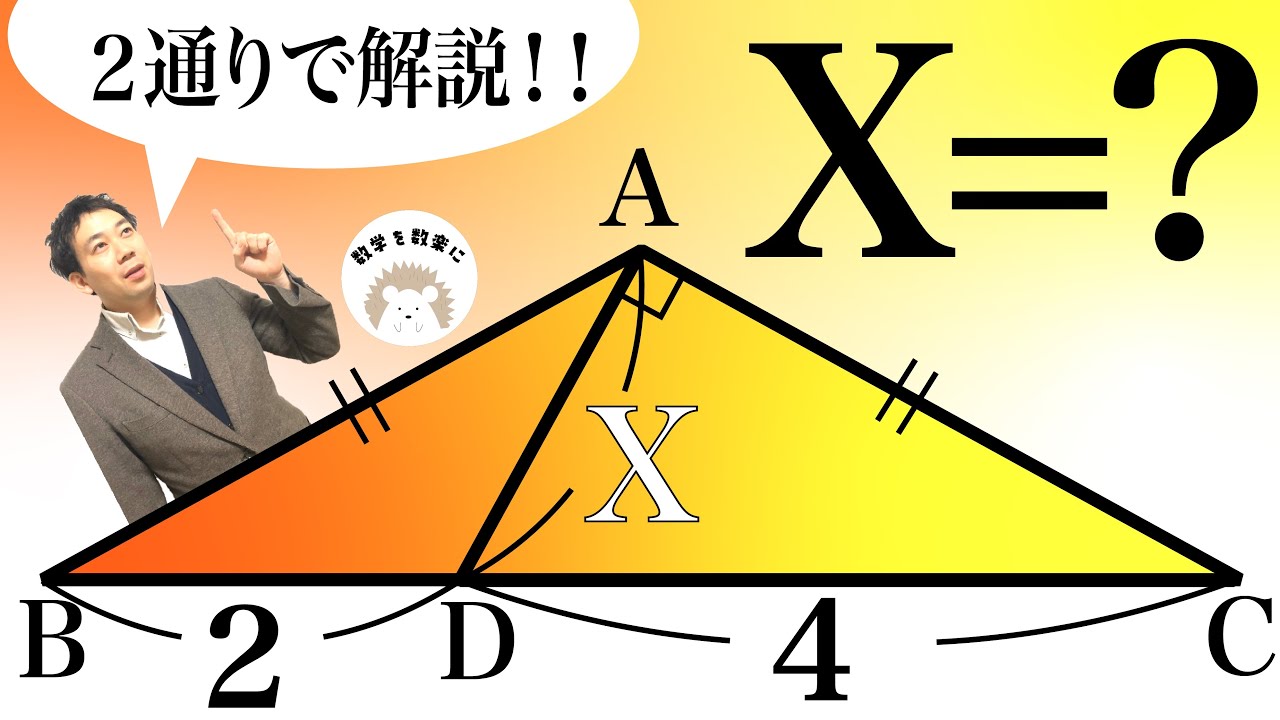
$\angle x $の大きさは？
①$20^\circ$
②$22.5^\circ$
③$25^\circ$
④$27.5^\circ$
⑤$30^\circ$
花巻東高等学校

単元： #数A#図形の性質#数学(高校生)

指導講師：数学を数楽に

問題文全文(内容文)：
$\angle x $の大きさは？
①$20^\circ$
②$22.5^\circ$
③$25^\circ$
④$27.5^\circ$
⑤$30^\circ$
花巻東高等学校

投稿日：2023.08.13

単元： #数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#旭川医科大学#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
旭川医科大学過去問題
a,b,cはどの2つも互いに素な自然数。$a^2+b^2=c^2$を満たすとき、次の(1)～(3)を示せ。
(1)cは奇数である
(2)a,bの1つは3の倍数
(3)a,bの1つは4の倍数

この動画を見る　

単元： #数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)

指導講師：数学を数楽に

問題文全文(内容文)：
20で割って、小数第一位を四捨五入すると17になるような最大の整数と最小の整数を求めよ

この動画を見る　

単元： #数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#数学(高校生)

指導講師：数学を数楽に

問題文全文(内容文)：
$\angle AED = ?$
＊図は動画内参照

この動画を見る　

単元： #数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#その他

指導講師：ますただ

問題文全文(内容文)：
$x,y \leftarrow in$
$\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6},x+y$の最大値を求めよ.

19神奈川県教員採用試験（数学：整数問題）過去問

この動画を見る　

単元： #数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
$x^4+x^3+x^2+x+1=0$のとき,
$\dfrac{x}{1+x^2}+\dfrac{x^2}{1+x^4}+\dfrac{x^3}{1+x}+\dfrac{x^4}{1+x^3}$の値を求めよ.

この動画を見る　