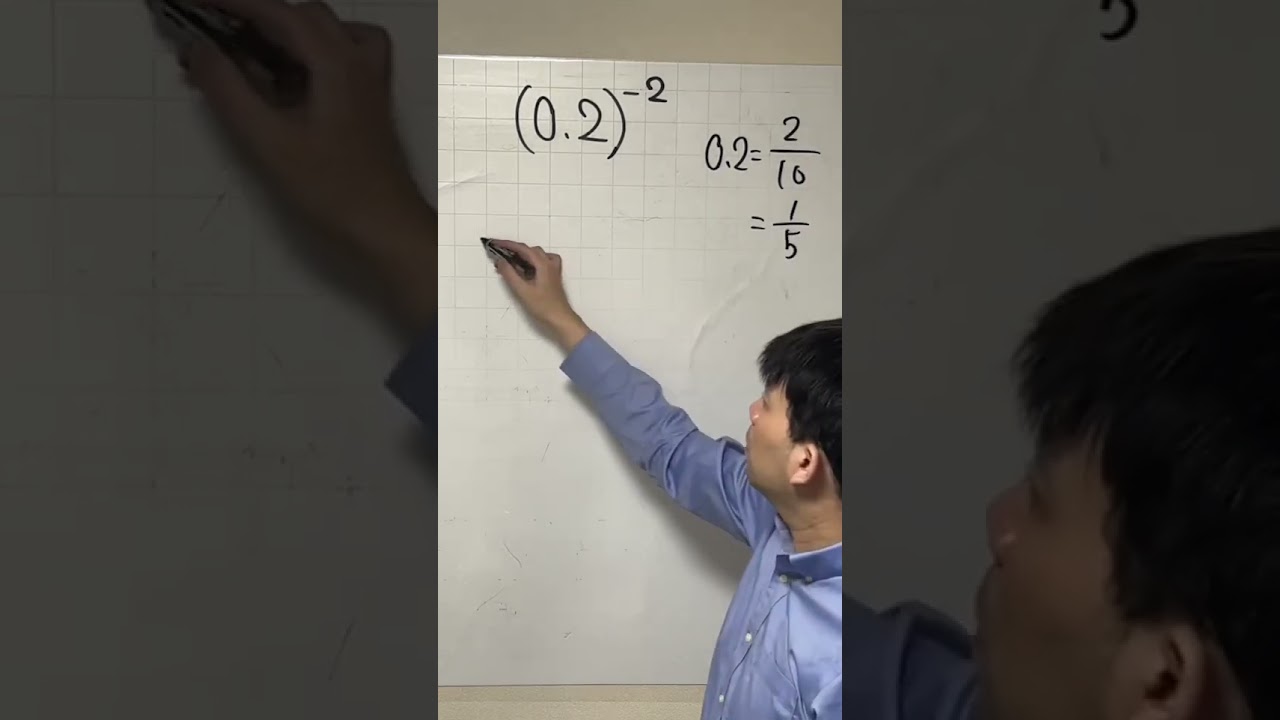問題文全文(内容文):
①
$e=\displaystyle \lim_{ x \to \infty }(1+\displaystyle \frac{1}{n})^n$
$=\displaystyle \lim_{ h \to \infty }(1+h)^{\displaystyle \frac{1}{h}}$
②
$y=e^x$ $y^1=e^x$
③
動画内の図をみて求めよ
④
$y=log_{e}x$
$y^1=\displaystyle \frac{1}{x}$
①
$e=\displaystyle \lim_{ x \to \infty }(1+\displaystyle \frac{1}{n})^n$
$=\displaystyle \lim_{ h \to \infty }(1+h)^{\displaystyle \frac{1}{h}}$
②
$y=e^x$ $y^1=e^x$
③
動画内の図をみて求めよ
④
$y=log_{e}x$
$y^1=\displaystyle \frac{1}{x}$
単元:
#数Ⅱ#指数関数と対数関数#指数関数#対数関数#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
①
$e=\displaystyle \lim_{ x \to \infty }(1+\displaystyle \frac{1}{n})^n$
$=\displaystyle \lim_{ h \to \infty }(1+h)^{\displaystyle \frac{1}{h}}$
②
$y=e^x$ $y^1=e^x$
③
動画内の図をみて求めよ
④
$y=log_{e}x$
$y^1=\displaystyle \frac{1}{x}$
①
$e=\displaystyle \lim_{ x \to \infty }(1+\displaystyle \frac{1}{n})^n$
$=\displaystyle \lim_{ h \to \infty }(1+h)^{\displaystyle \frac{1}{h}}$
②
$y=e^x$ $y^1=e^x$
③
動画内の図をみて求めよ
④
$y=log_{e}x$
$y^1=\displaystyle \frac{1}{x}$
投稿日:2019.03.09