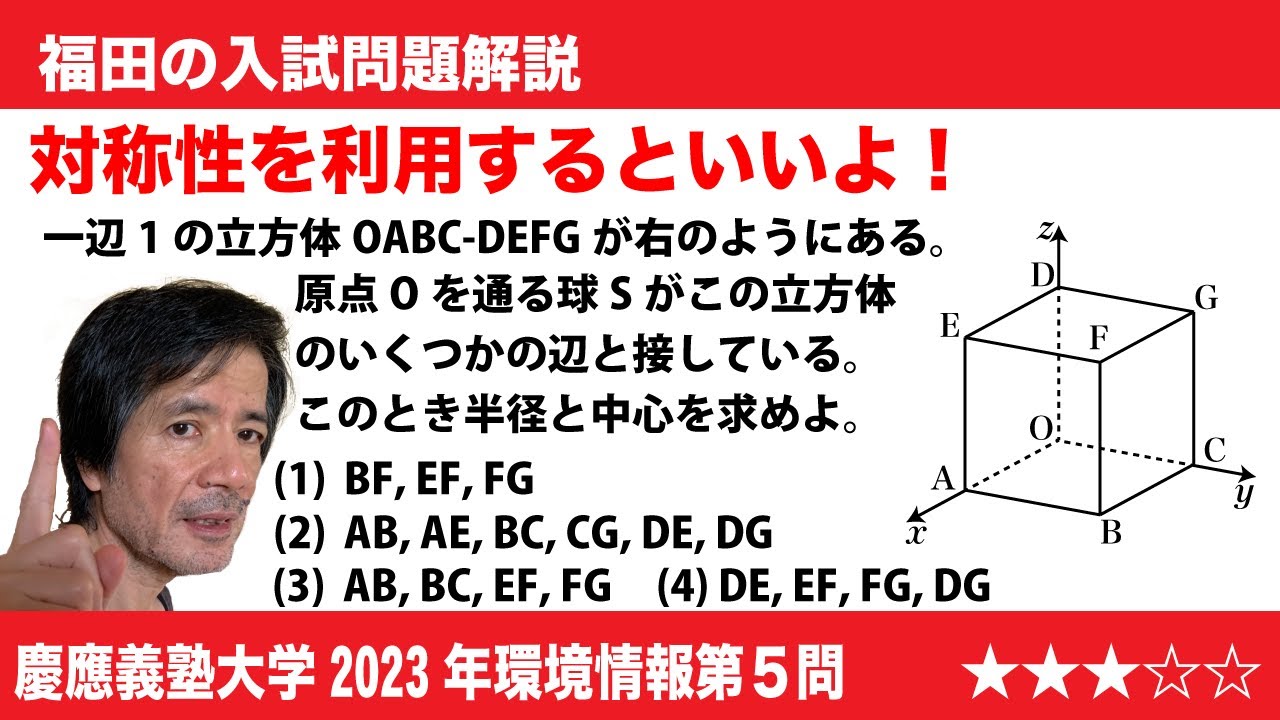
問題文全文(内容文):
〔Ⅲ〕$x+2y=5、x\gt 0,y\gt 0$を満たす実数x,yがある。
(1) $2x^2+y^2$の最小値
(2) $\log_{10}x+2\log_{10}y$ の最大値
(3) $\dfrac{1}{x}+\dfrac{2}{y}$ の最小値
〔Ⅲ〕$x+2y=5、x\gt 0,y\gt 0$を満たす実数x,yがある。
(1) $2x^2+y^2$の最小値
(2) $\log_{10}x+2\log_{10}y$ の最大値
(3) $\dfrac{1}{x}+\dfrac{2}{y}$ の最小値
チャプター:
0:00 オープニング
0:20 (1)の問題分析
1:32 最小値の求め方
3:10 まとめ
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
〔Ⅲ〕$x+2y=5、x\gt 0,y\gt 0$を満たす実数x,yがある。
(1) $2x^2+y^2$の最小値
(2) $\log_{10}x+2\log_{10}y$ の最大値
(3) $\dfrac{1}{x}+\dfrac{2}{y}$ の最小値
〔Ⅲ〕$x+2y=5、x\gt 0,y\gt 0$を満たす実数x,yがある。
(1) $2x^2+y^2$の最小値
(2) $\log_{10}x+2\log_{10}y$ の最大値
(3) $\dfrac{1}{x}+\dfrac{2}{y}$ の最小値
備考:【数Ⅰ】明治大学経営学部(2019年)数学第3問 ①
https://youtu.be/iOXnwxxf_ZI
【数Ⅱ】明治大学経営学部入試問題2019年数学第3問②
https://youtu.be/hM41zIUOtdw
【数Ⅱ】明治大学経営学部入試問題2019年数学第3問③
https://youtu.be/sfECgtn4R74
https://youtu.be/iOXnwxxf_ZI
【数Ⅱ】明治大学経営学部入試問題2019年数学第3問②
https://youtu.be/hM41zIUOtdw
【数Ⅱ】明治大学経営学部入試問題2019年数学第3問③
https://youtu.be/sfECgtn4R74
投稿日:2022.03.18