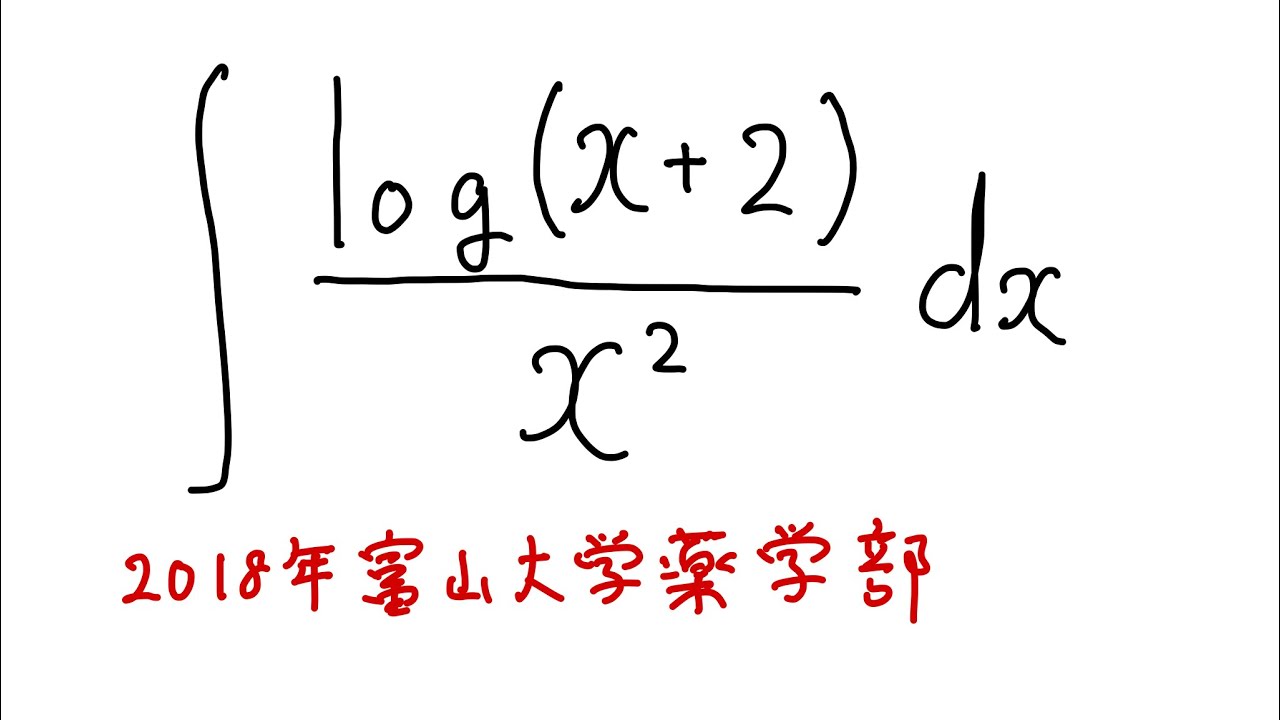大学受験過去問シリーズ！横浜国立大2019年（理系）第4問の解説 #数学 #過去問 #横浜国立大学

問題文全文(内容文)：
横浜国立大2019年（理系）第4問の解説していきます.

単元： #大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)

指導講師：理数個別チャンネル

問題文全文(内容文)：
横浜国立大2019年（理系）第4問の解説していきます.

投稿日：2024.02.05

単元： #大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
n個のボールを3つの箱に入れる場合の数,
(1)ボールの色はすべて異なり,箱にも名前有.
(2)ボールは区別できない,箱は区別できる.
(3)ボールは区別,箱は区別しない.
(4)6m区別なし,箱も区別なし.

東大過去問

この動画を見る　

単元： #数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)

指導講師：福田次郎

問題文全文(内容文)：
正の実数tに対し、座標平面上の2点$P(0,t)$と$Q(\frac{1}{t},0)$を考える。
tが$1 \leqq t \leqq 2$の範囲を動くとき、座標平面内で線分PQが通過する部分を図示せよ。

2022大阪大学理系過去問

この動画を見る　

単元： #数Ⅰ#大学入試過去問(数学)#数と式#式の計算（整式・展開・因数分解）#学校別大学入試過去問解説(数学)#数学(高校生)

指導講師：数学を数楽に

問題文全文(内容文)：
因数分解せよ
$x^4+x^2+1+2xy-y^2$

福島大学

この動画を見る　

単元： #数Ⅱ#大学入試過去問(数学)#微分法と積分法#一橋大学#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
2007一橋大学過去問題
aを定数とし、$f(x)=x^3-3ax^2+a$とする。
$x \leqq 2$の範囲でf(x)の最大値が105となるようなaをすべて求めよ。

この動画を見る　

単元： #数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#富山大学#数Ⅲ

指導講師：ますただ

問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{log(x+2)}{x^2} dx$

出典：2018年富山大学薬学部

この動画を見る　