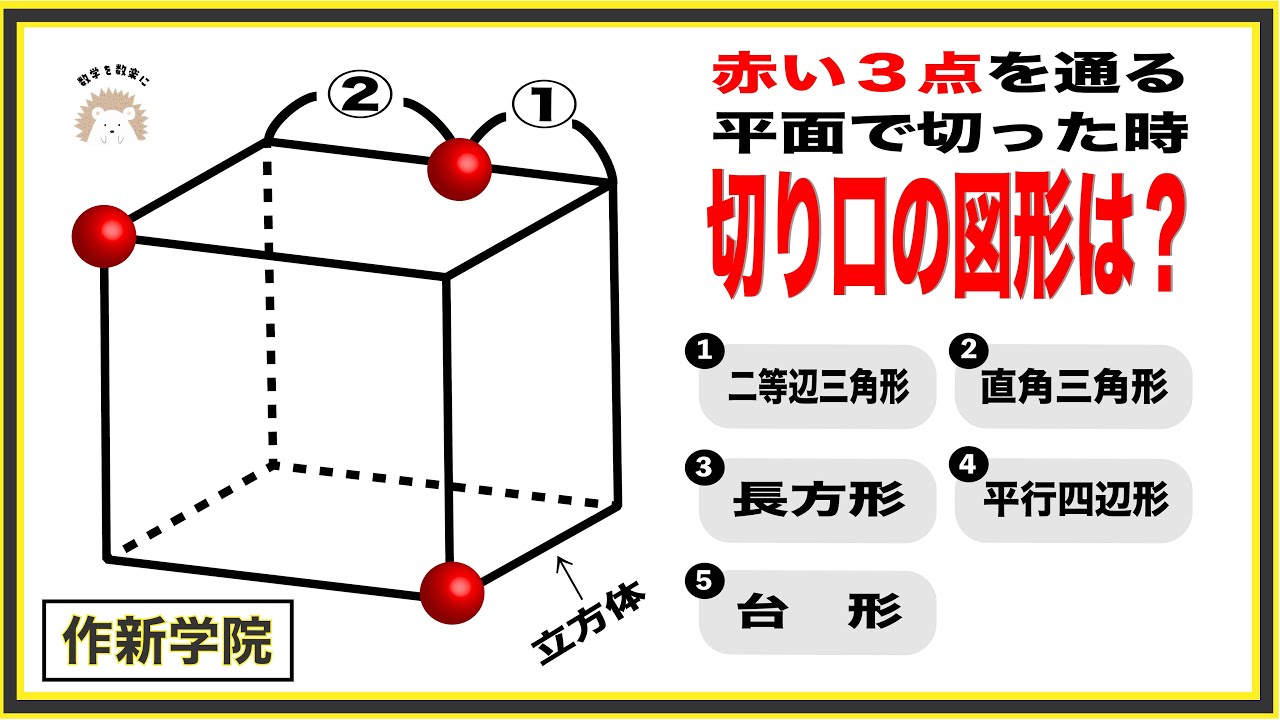
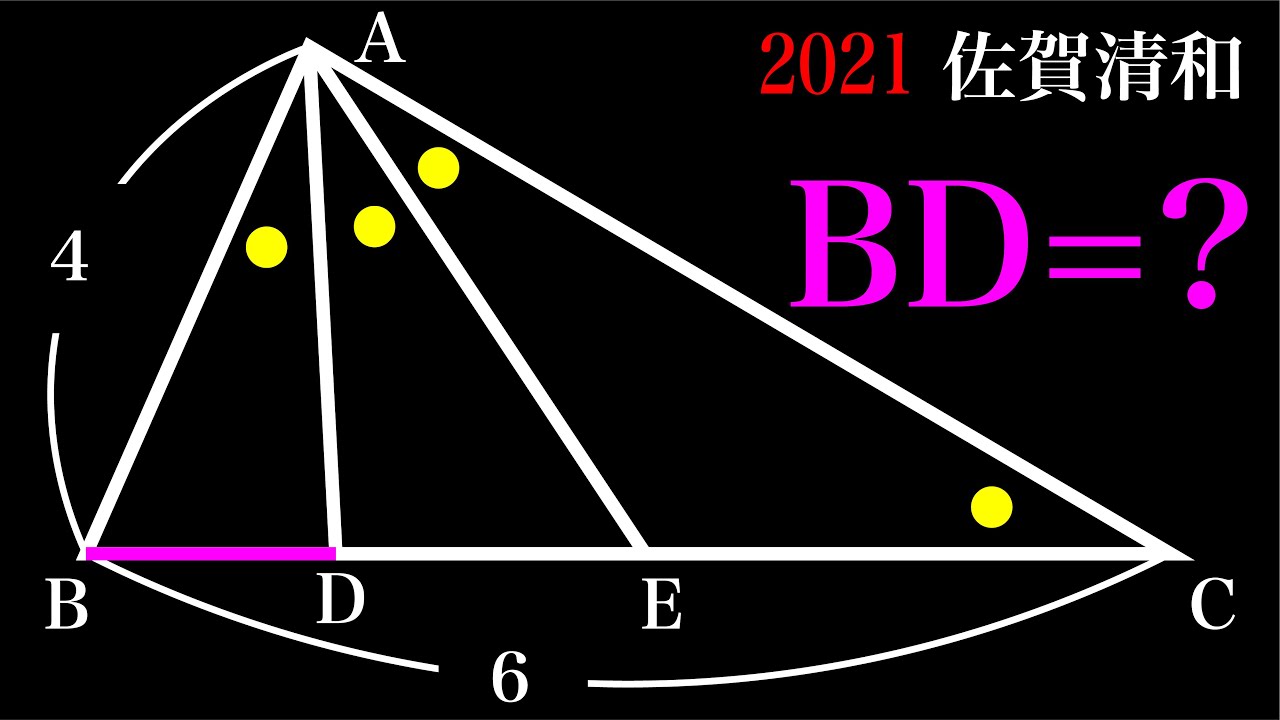
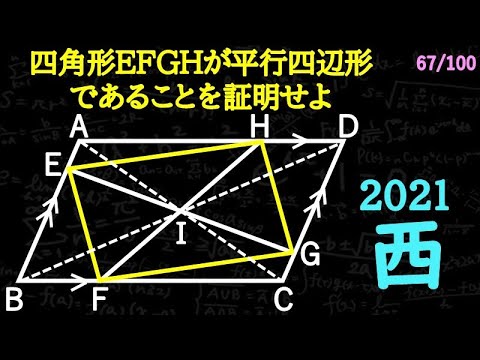
問題文全文(内容文):
高校受験対策・難解死守4
①連立方程式を解け
$\frac{2x-y}{3}=\frac{y}{2}-1$
$(x+1):(y-2)=3:4$
➁$3\sqrt{8}-\frac{\sqrt{3}}{2}-\sqrt{2}+\sqrt{75}$
③$x,y,z$を$0$以上の整数とするとき、$x+2y+3z=20$を満たす整数の組$(x,y,z)$は何組あるか。
④$x^2yz-y^3z+2y^2z^2-yz^3$を因数分解せよ。
⑤大中小3つのさいころを同時に1回投げて、大中小のさいころの出た目の数をそれぞれ$a,b,c$とする。
このとき$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$となる確率を求めよ。
⑥右の図のように、円$o$の周上に5点、$A,B,C,D,E$をとる。
線分$AC$は 円$o$の直径であり、$\stackrel{\huge\frown}{BC}=\stackrel{\huge\frown}{CD}=\stackrel{\huge\frown}{DE}$、$\angle BAC=15°$である。
線分$AC$と$BE$の交点を$F$とするとき、$\angle AFE$の大きさを求めよ。
高校受験対策・難解死守4
①連立方程式を解け
$\frac{2x-y}{3}=\frac{y}{2}-1$
$(x+1):(y-2)=3:4$
➁$3\sqrt{8}-\frac{\sqrt{3}}{2}-\sqrt{2}+\sqrt{75}$
③$x,y,z$を$0$以上の整数とするとき、$x+2y+3z=20$を満たす整数の組$(x,y,z)$は何組あるか。
④$x^2yz-y^3z+2y^2z^2-yz^3$を因数分解せよ。
⑤大中小3つのさいころを同時に1回投げて、大中小のさいころの出た目の数をそれぞれ$a,b,c$とする。
このとき$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$となる確率を求めよ。
⑥右の図のように、円$o$の周上に5点、$A,B,C,D,E$をとる。
線分$AC$は 円$o$の直径であり、$\stackrel{\huge\frown}{BC}=\stackrel{\huge\frown}{CD}=\stackrel{\huge\frown}{DE}$、$\angle BAC=15°$である。
線分$AC$と$BE$の交点を$F$とするとき、$\angle AFE$の大きさを求めよ。
単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・難解死守4
①連立方程式を解け
$\frac{2x-y}{3}=\frac{y}{2}-1$
$(x+1):(y-2)=3:4$
➁$3\sqrt{8}-\frac{\sqrt{3}}{2}-\sqrt{2}+\sqrt{75}$
③$x,y,z$を$0$以上の整数とするとき、$x+2y+3z=20$を満たす整数の組$(x,y,z)$は何組あるか。
④$x^2yz-y^3z+2y^2z^2-yz^3$を因数分解せよ。
⑤大中小3つのさいころを同時に1回投げて、大中小のさいころの出た目の数をそれぞれ$a,b,c$とする。
このとき$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$となる確率を求めよ。
⑥右の図のように、円$o$の周上に5点、$A,B,C,D,E$をとる。
線分$AC$は 円$o$の直径であり、$\stackrel{\huge\frown}{BC}=\stackrel{\huge\frown}{CD}=\stackrel{\huge\frown}{DE}$、$\angle BAC=15°$である。
線分$AC$と$BE$の交点を$F$とするとき、$\angle AFE$の大きさを求めよ。
高校受験対策・難解死守4
①連立方程式を解け
$\frac{2x-y}{3}=\frac{y}{2}-1$
$(x+1):(y-2)=3:4$
➁$3\sqrt{8}-\frac{\sqrt{3}}{2}-\sqrt{2}+\sqrt{75}$
③$x,y,z$を$0$以上の整数とするとき、$x+2y+3z=20$を満たす整数の組$(x,y,z)$は何組あるか。
④$x^2yz-y^3z+2y^2z^2-yz^3$を因数分解せよ。
⑤大中小3つのさいころを同時に1回投げて、大中小のさいころの出た目の数をそれぞれ$a,b,c$とする。
このとき$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$となる確率を求めよ。
⑥右の図のように、円$o$の周上に5点、$A,B,C,D,E$をとる。
線分$AC$は 円$o$の直径であり、$\stackrel{\huge\frown}{BC}=\stackrel{\huge\frown}{CD}=\stackrel{\huge\frown}{DE}$、$\angle BAC=15°$である。
線分$AC$と$BE$の交点を$F$とするとき、$\angle AFE$の大きさを求めよ。
投稿日:2020.02.06