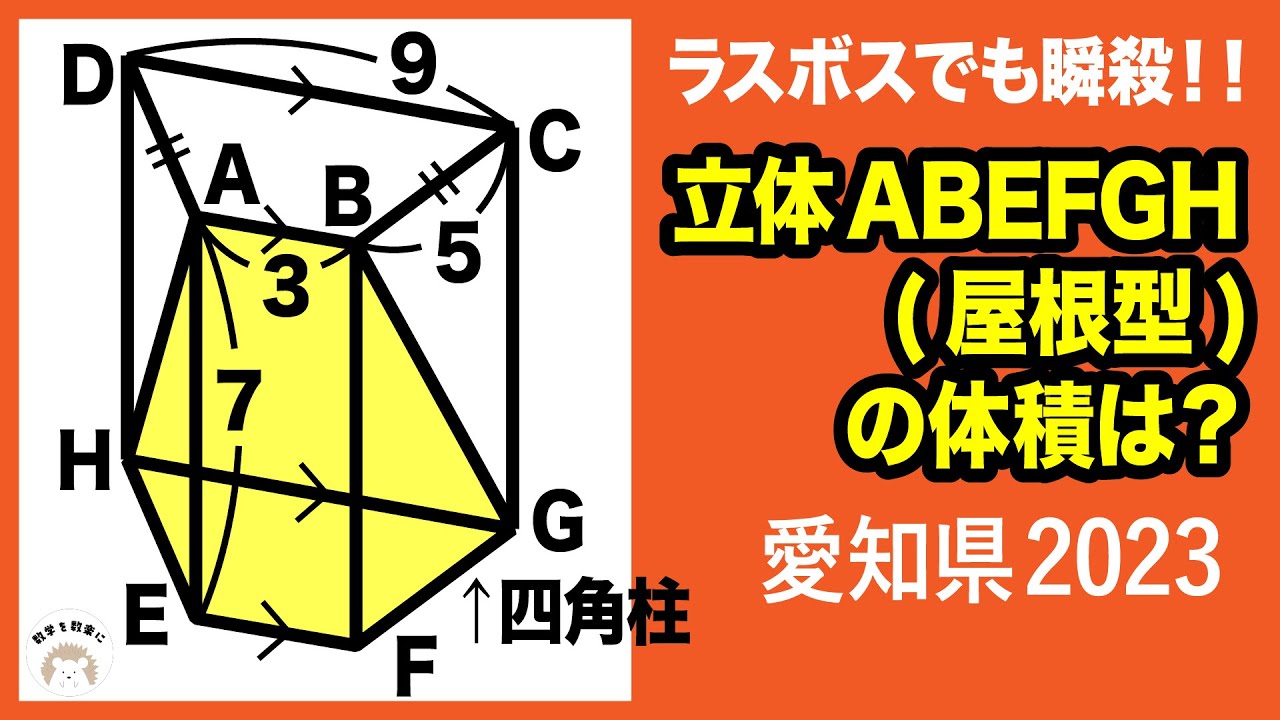
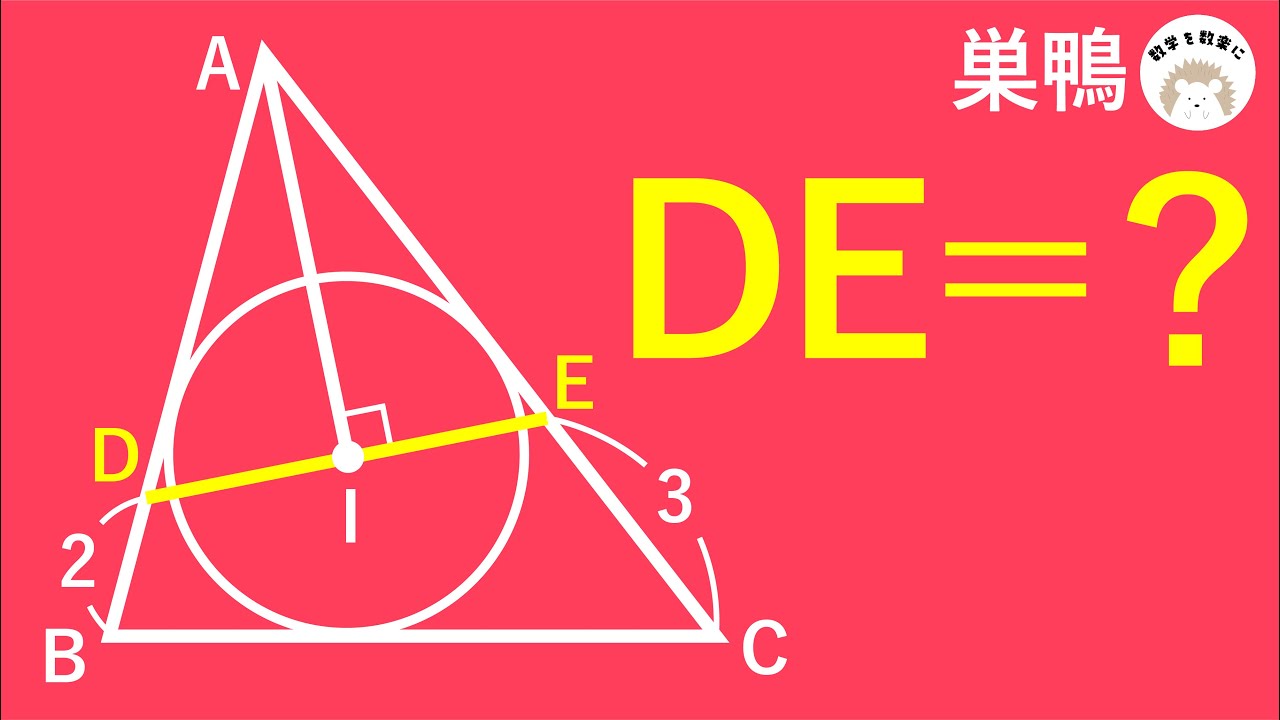
問題文全文(内容文):
高校受験対策 数学・死守48
①$-7+3-4$を計算しなさい。
➁$\frac{1}{3} \div(-\frac{1}{6})$を計算しなさい。
③$\frac{3}{\sqrt{3}}+4\sqrt{3}-\sqrt{27}$を計算しなさい。
④$4(2x-1)-3(2x-3)$を計算しなさい。
⑤$(-xy)^2 \times 10xy^2 \div 5x^2$を計算しなさい。
⑥$(3x-1)(4x+3)$を展開しなさい。
⑦$x^2-4x+3$を因数分解しなさい。
⑧$a=-3$のとき、$a^2-2a$の値を求めなさい。
⑨等式を$V=\pi r^2h$$h$について解きなさい。
➉二次方程式$sx^2+3x-1=0$を解きなさい。
⑪
右の図1において、3点A,B,Cは点Oを中心とする円の周上の点である。
このとき、$∠x$の大きさを求めなさい。
⑫
右の図2のように、直線$l$上に2点O,Aがあり、OA=1とする。
このとき$OP=\sqrt{2}$となる点Pを、以下の指示に従って作図しなさい。
指示
・点Pは点Oよりも右側にとりなさい。
・作図に用いた線は消さずに残しておきなさい。
・作図した点Pには記号を書き入れなさい。
高校受験対策 数学・死守48
①$-7+3-4$を計算しなさい。
➁$\frac{1}{3} \div(-\frac{1}{6})$を計算しなさい。
③$\frac{3}{\sqrt{3}}+4\sqrt{3}-\sqrt{27}$を計算しなさい。
④$4(2x-1)-3(2x-3)$を計算しなさい。
⑤$(-xy)^2 \times 10xy^2 \div 5x^2$を計算しなさい。
⑥$(3x-1)(4x+3)$を展開しなさい。
⑦$x^2-4x+3$を因数分解しなさい。
⑧$a=-3$のとき、$a^2-2a$の値を求めなさい。
⑨等式を$V=\pi r^2h$$h$について解きなさい。
➉二次方程式$sx^2+3x-1=0$を解きなさい。
⑪
右の図1において、3点A,B,Cは点Oを中心とする円の周上の点である。
このとき、$∠x$の大きさを求めなさい。
⑫
右の図2のように、直線$l$上に2点O,Aがあり、OA=1とする。
このとき$OP=\sqrt{2}$となる点Pを、以下の指示に従って作図しなさい。
指示
・点Pは点Oよりも右側にとりなさい。
・作図に用いた線は消さずに残しておきなさい。
・作図した点Pには記号を書き入れなさい。
単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策 数学・死守48
①$-7+3-4$を計算しなさい。
➁$\frac{1}{3} \div(-\frac{1}{6})$を計算しなさい。
③$\frac{3}{\sqrt{3}}+4\sqrt{3}-\sqrt{27}$を計算しなさい。
④$4(2x-1)-3(2x-3)$を計算しなさい。
⑤$(-xy)^2 \times 10xy^2 \div 5x^2$を計算しなさい。
⑥$(3x-1)(4x+3)$を展開しなさい。
⑦$x^2-4x+3$を因数分解しなさい。
⑧$a=-3$のとき、$a^2-2a$の値を求めなさい。
⑨等式を$V=\pi r^2h$$h$について解きなさい。
➉二次方程式$sx^2+3x-1=0$を解きなさい。
⑪
右の図1において、3点A,B,Cは点Oを中心とする円の周上の点である。
このとき、$∠x$の大きさを求めなさい。
⑫
右の図2のように、直線$l$上に2点O,Aがあり、OA=1とする。
このとき$OP=\sqrt{2}$となる点Pを、以下の指示に従って作図しなさい。
指示
・点Pは点Oよりも右側にとりなさい。
・作図に用いた線は消さずに残しておきなさい。
・作図した点Pには記号を書き入れなさい。
高校受験対策 数学・死守48
①$-7+3-4$を計算しなさい。
➁$\frac{1}{3} \div(-\frac{1}{6})$を計算しなさい。
③$\frac{3}{\sqrt{3}}+4\sqrt{3}-\sqrt{27}$を計算しなさい。
④$4(2x-1)-3(2x-3)$を計算しなさい。
⑤$(-xy)^2 \times 10xy^2 \div 5x^2$を計算しなさい。
⑥$(3x-1)(4x+3)$を展開しなさい。
⑦$x^2-4x+3$を因数分解しなさい。
⑧$a=-3$のとき、$a^2-2a$の値を求めなさい。
⑨等式を$V=\pi r^2h$$h$について解きなさい。
➉二次方程式$sx^2+3x-1=0$を解きなさい。
⑪
右の図1において、3点A,B,Cは点Oを中心とする円の周上の点である。
このとき、$∠x$の大きさを求めなさい。
⑫
右の図2のように、直線$l$上に2点O,Aがあり、OA=1とする。
このとき$OP=\sqrt{2}$となる点Pを、以下の指示に従って作図しなさい。
指示
・点Pは点Oよりも右側にとりなさい。
・作図に用いた線は消さずに残しておきなさい。
・作図した点Pには記号を書き入れなさい。
投稿日:2020.01.03