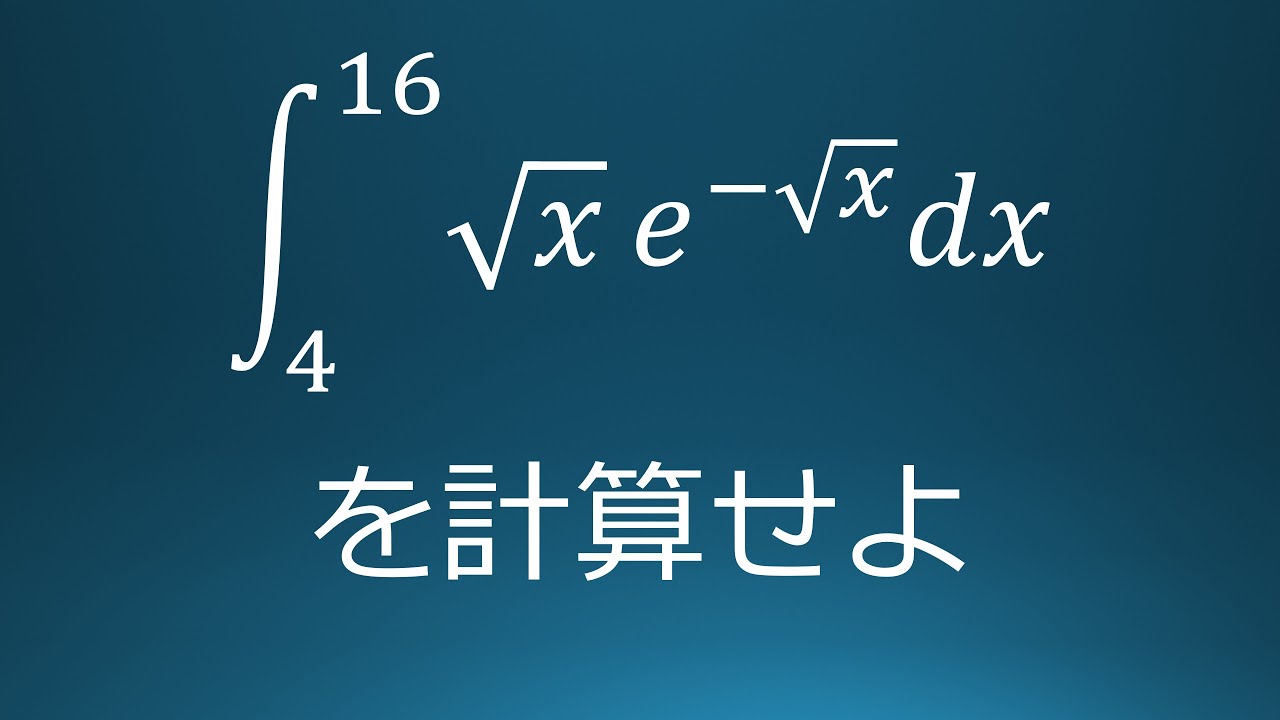大学入試問題#391「正面突破が王道だと思いますが、あえて」東北学院大学(2009) #定積分

問題文全文(内容文)：
$\displaystyle \int_{0}^{\pi} (\sin^3x-\cos^3x) dx$

出典：2009年東北学院大学　入試問題

チャプター：

00:00 問題紹介
00:10 本編スタート
05:35 作成した解答①
05:45 作成した解答②
05:56 エンディング（楽曲提供：兄いえてぃさん）

単元： #積分とその応用#定積分#数学(高校生)#数Ⅲ

指導講師：ますただ

問題文全文(内容文)：
$\displaystyle \int_{0}^{\pi} (\sin^3x-\cos^3x) dx$

出典：2009年東北学院大学　入試問題

投稿日：2022.12.10

単元： #積分とその応用#定積分#数学(高校生)#数Ⅲ

指導講師：理数個別チャンネル

問題文全文(内容文)：
$\int_0^{\frac{π}{4}}\frac{dx}{cos^3x}$
これを解け.

この動画を見る　

単元： #積分とその応用#定積分#数学(高校生)#数Ⅲ

指導講師：理数個別チャンネル

問題文全文(内容文)：
$\int_{-\sqrt{2}}^{\sqrt{2}}\frac{8}{x^4+4}dx$
(3)前の結果を用いて計算せよ

この動画を見る　

単元： #積分とその応用#定積分#数学(高校生)#数Ⅲ

指導講師：ますただ

問題文全文(内容文)：
$\displaystyle \int_{-\frac{1}{2}}^{\frac{2}{3}}\displaystyle \frac{dx}{\sqrt{ x^3-3x+2 }}$を求めよ。

この動画を見る　

単元： #積分とその応用#定積分#数学(高校生)#数Ⅲ

指導講師：理数個別チャンネル

問題文全文(内容文)：
$\int_1^4\frac{dx}{\sqrt{3-\sqrt{x}}}$
これを解け.

この動画を見る　

単元： #数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定1級#数学(高校生)#数Ⅲ

指導講師：ますただ

問題文全文(内容文)：
$\displaystyle \int_{0}^{\infty}\displaystyle \frac{1}{(x^2+1)^4}\ dx$を計算せよ。

この動画を見る　