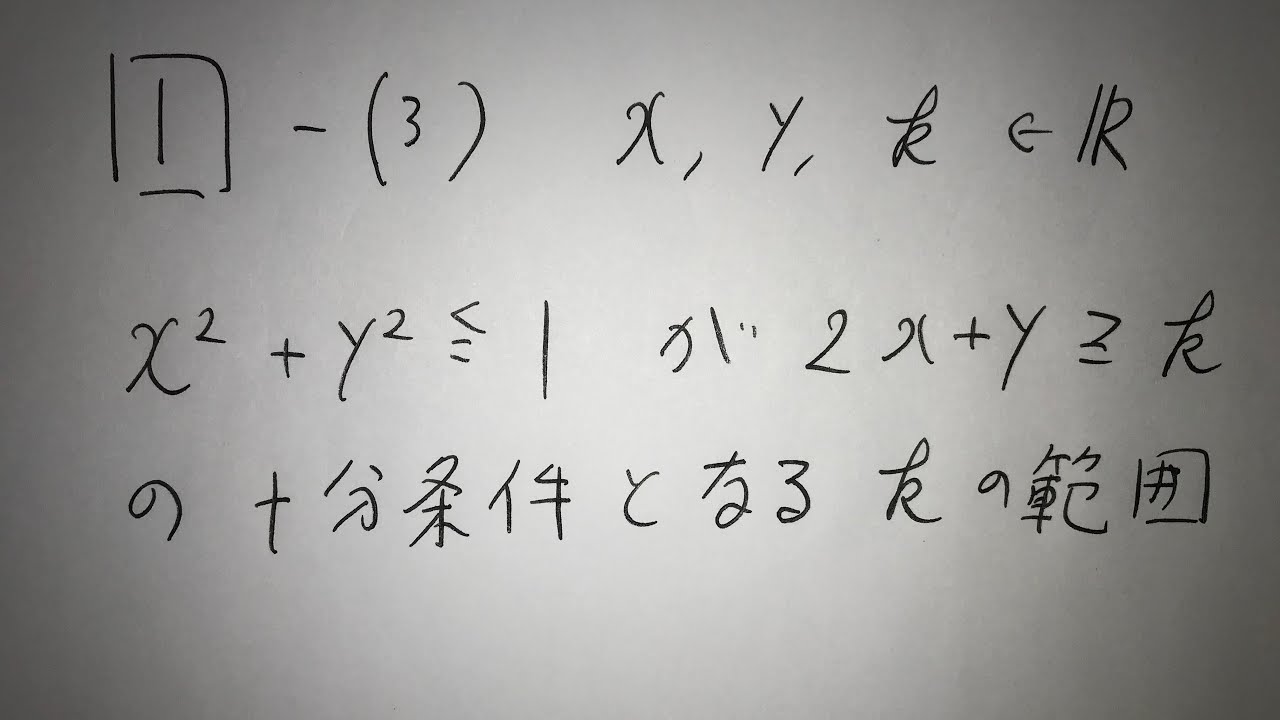問題文全文(内容文):
$\sin\theta-\cos\theta$を$\sin\theta$だけを用いた式で表せ。また,$\cos\theta$だけを用いた式で表せ。
$\sin\theta-\cos\theta$を$\sin\theta$だけを用いた式で表せ。また,$\cos\theta$だけを用いた式で表せ。
チャプター:
0:00 オープニング
0:17 sinだけ
2:55 cosだけ
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\sin\theta-\cos\theta$を$\sin\theta$だけを用いた式で表せ。また,$\cos\theta$だけを用いた式で表せ。
$\sin\theta-\cos\theta$を$\sin\theta$だけを用いた式で表せ。また,$\cos\theta$だけを用いた式で表せ。
投稿日:2024.11.20