これ裏技？ - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(中学生) > 中３数学 > ２次方程式 > これ裏技？

これ裏技？

問題文全文(内容文)：
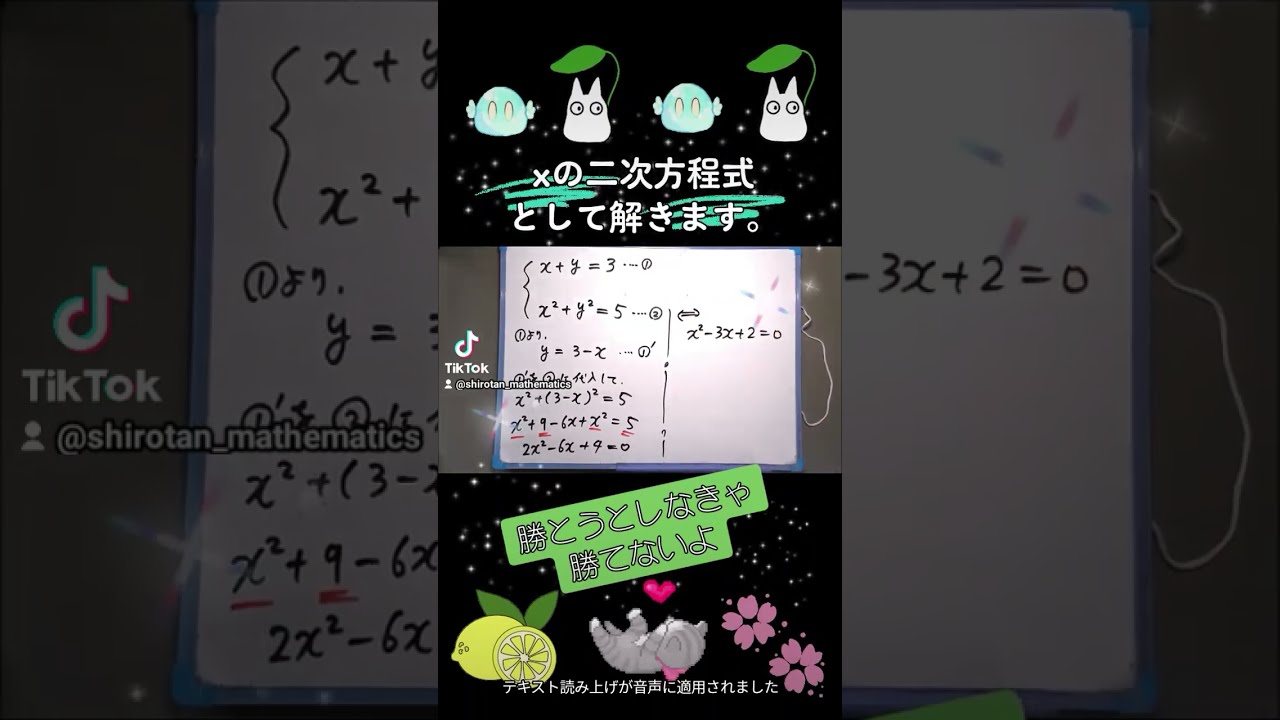
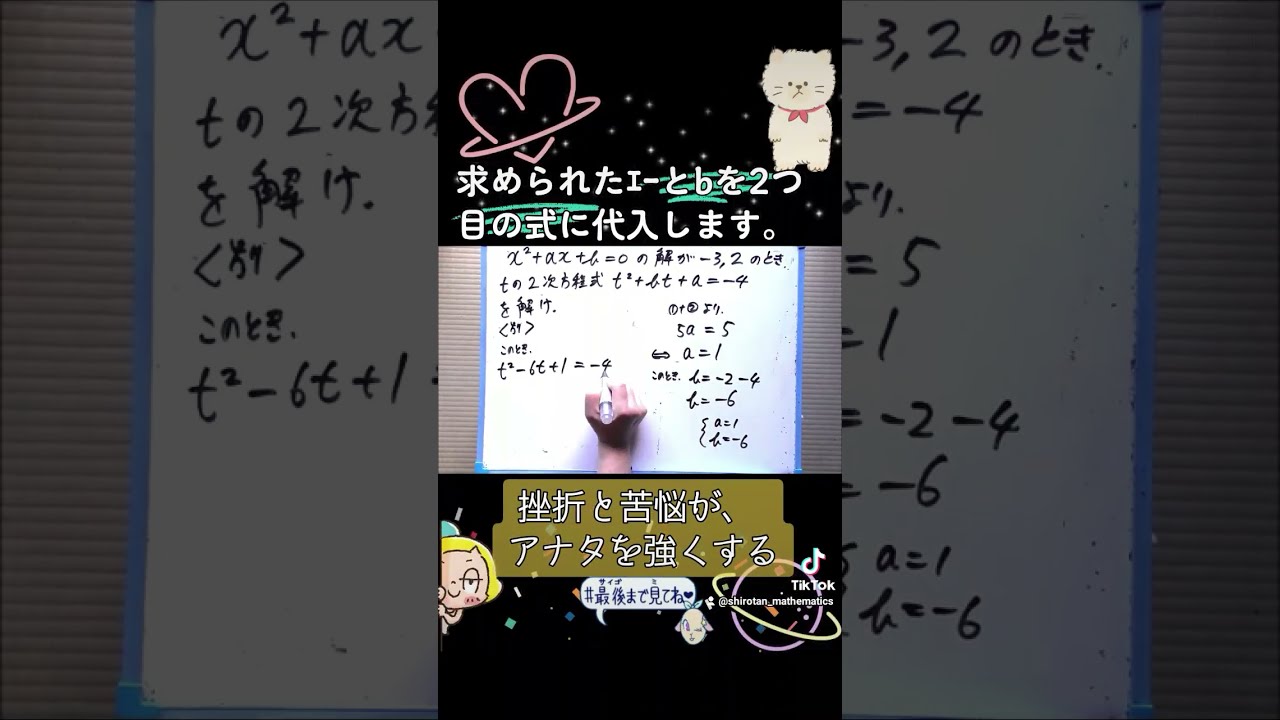
2次関数上の2点を通る直線の方程式を素早く求める方法についての動画です。
単元： #数学(中学生)#中３数学#２次方程式
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
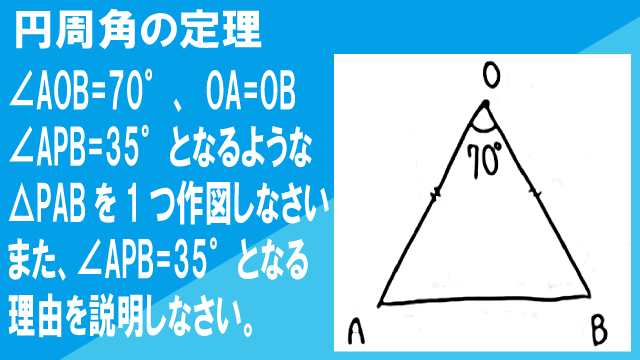
2次関数上の2点を通る直線の方程式を素早く求める方法についての動画です。
投稿日：2024.10.17

＜関連動画＞

【テスト対策・中３】２章－２

アイキャッチ画像
単元： #数学(中学生)#中３数学#平方根
指導講師： とある男が授業をしてみた
問題文全文(内容文)：
①$\sqrt{20}$と$\sqrt{18}+\sqrt2$はどちらが大きいか,
理由をあわせて説明しなさい.

②$\sqrt{17},2\sqrt3,\dfrac{6}{\sqrt2},\sqrt{(-4)^2}$を
小さい順に左から並べなさい.
この動画を見る　

【テスト対策・中３】１章－１

アイキャッチ画像
単元： #数学(中学生)#中３数学#式の計算（展開、因数分解）
指導講師： とある男が授業をしてみた
問題文全文(内容文)：
次の式を簡単にしなさい.

①$(x+5)^2-2(x+4)(x+1)$

②$-(2x+3)(2x-1)+(3x-1)^2$

③$(x^2+5x+1)(x^2-5x+1)$

④$(-2a-3b+c)^2-(2a+3b)(2a+3b-2c)$

⑤$(x-1)(x-2)(x-3)(x-4)$
この動画を見る　

視聴者さんの別解コメントありがたい

アイキャッチ画像
単元： #数学(中学生)#中３数学#式の計算（展開、因数分解）
指導講師： 数学を数楽に
問題文全文(内容文)：
$abx^2-(a^2+b^2)x+ab$を因数分解
この動画を見る　

【見た目よりカンタン…！】文字式：日本大学第三高等学校～全国入試問題解法

アイキャッチ画像
単元： #数学(中学生)#中１数学#中３数学#平方根#文字と式
指導講師： 高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
x=√6,y=√2のとき
√(x-y)/√(x＋y) - √(x＋y)/√(x-y)
この式の値を求めなさい
この動画を見る　

【当たり前が大切だったと気づく瞬間！】二次関数：青森県公立高等学校～全国入試問題解法

アイキャッチ画像
単元： #数学(中学生)#中３数学#2次関数#高校入試過去問(数学)
指導講師： 高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
関数$y=ax^2$について
$x$の変域が$-2\leqq x \leqq 3$のとき,$y$の変域は$-6\leqq y\leqq 0$である.
このとき,$a$の値を求めなさい.

青森県公立高等学校過去問
この動画を見る　
Back to top