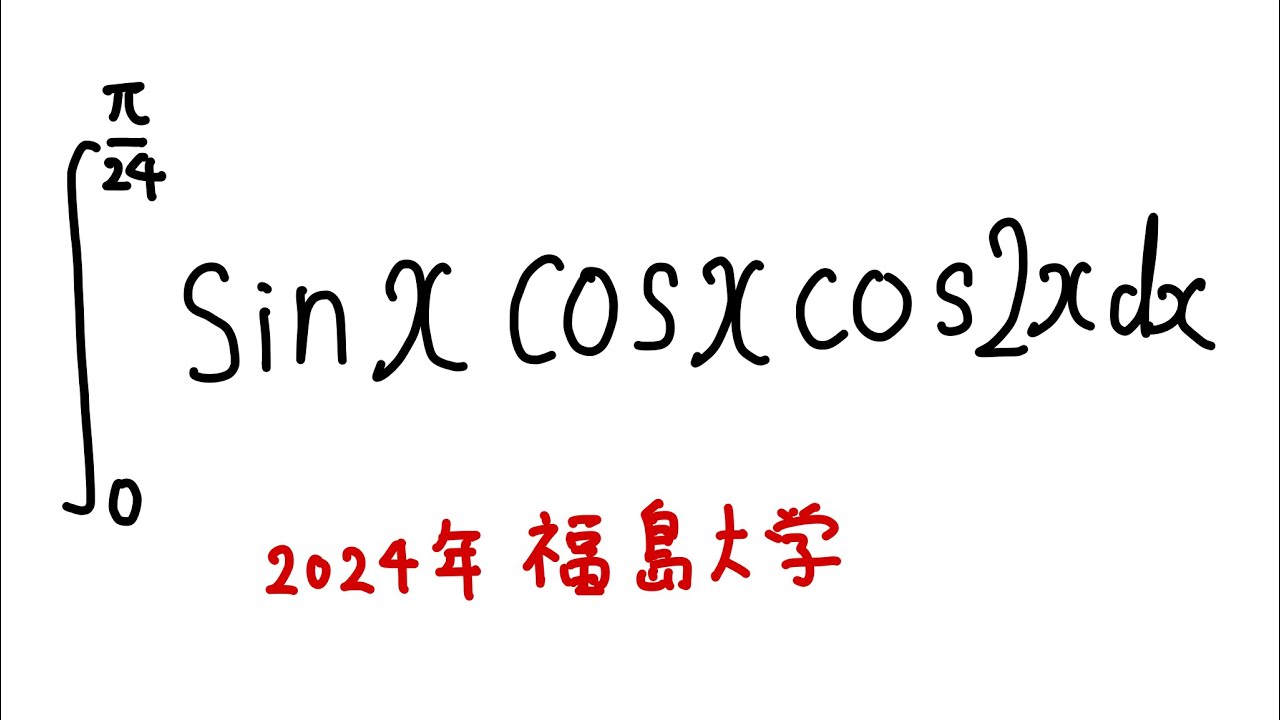問題文全文(内容文):
次の関数をxについて微分せよ。
(1)$F(x)=\displaystyle \int_{e}^{t}\sin t dt$
(2)$F(x)=\displaystyle \int_(x+t)e^t dt$
(出典 4S数学Ⅲより)
学校の問題集にも載っている問題の解説です。
定期テストなどの対策で活用してみてくださいね。
次の関数をxについて微分せよ。
(1)$F(x)=\displaystyle \int_{e}^{t}\sin t dt$
(2)$F(x)=\displaystyle \int_(x+t)e^t dt$
(出典 4S数学Ⅲより)
学校の問題集にも載っている問題の解説です。
定期テストなどの対策で活用してみてくださいね。
チャプター:
00:00 問題の紹介
00:22 (1)の解説
03:06 (2)の解説
単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学Ⅲ#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数をxについて微分せよ。
(1)$F(x)=\displaystyle \int_{e}^{t}\sin t dt$
(2)$F(x)=\displaystyle \int_(x+t)e^t dt$
(出典 4S数学Ⅲより)
学校の問題集にも載っている問題の解説です。
定期テストなどの対策で活用してみてくださいね。
次の関数をxについて微分せよ。
(1)$F(x)=\displaystyle \int_{e}^{t}\sin t dt$
(2)$F(x)=\displaystyle \int_(x+t)e^t dt$
(出典 4S数学Ⅲより)
学校の問題集にも載っている問題の解説です。
定期テストなどの対策で活用してみてくださいね。
投稿日:2023.01.11