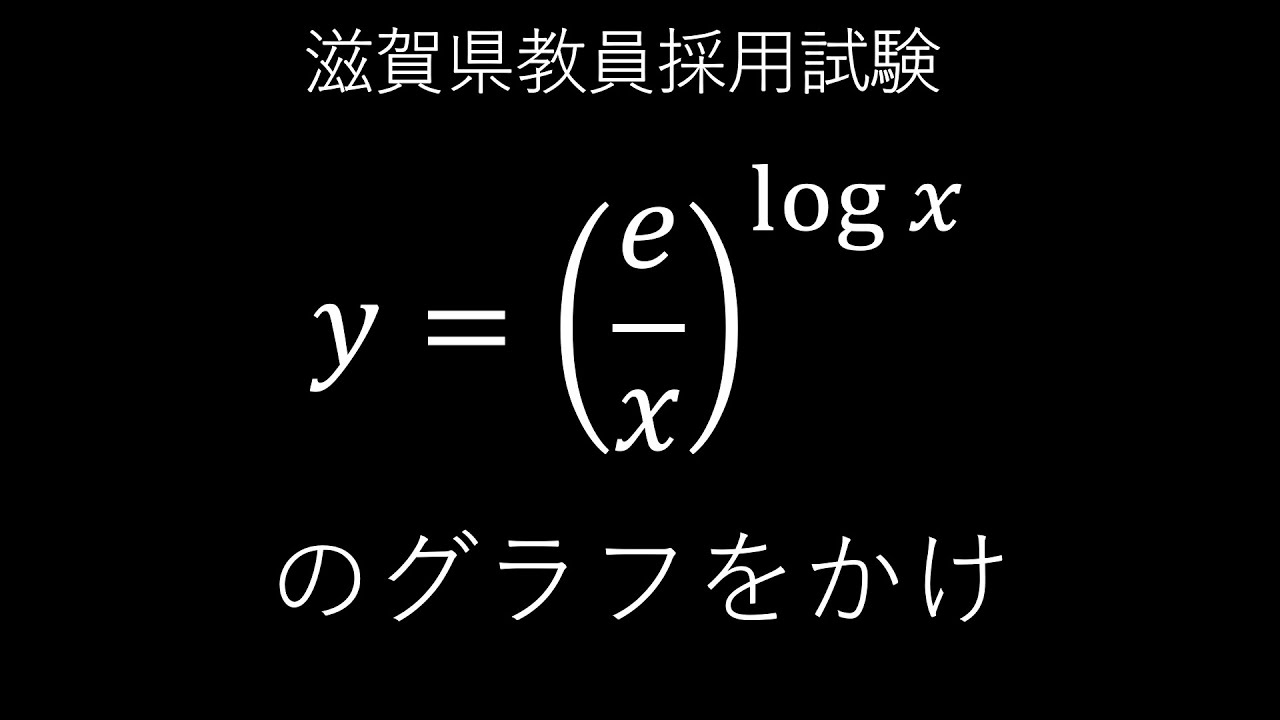問題文全文(内容文):
$z=f(x,y)$:全微分可能である.
$\dfrac{dz}{dt}$を$t,\dfrac{\delta z}{\delta x},\dfrac{\delta z}{\delta y}$で表せ.
(1)$x-te^t,y=\log t$
(2)$x=\dfrac{t}{2t+1},y=\dfrac{t+1}{2t+1}$
$z=f(x,y)$:全微分可能である.
$\dfrac{dz}{dt}$を$t,\dfrac{\delta z}{\delta x},\dfrac{\delta z}{\delta y}$で表せ.
(1)$x-te^t,y=\log t$
(2)$x=\dfrac{t}{2t+1},y=\dfrac{t+1}{2t+1}$
単元:
#数Ⅱ#微分法と積分法#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$z=f(x,y)$:全微分可能である.
$\dfrac{dz}{dt}$を$t,\dfrac{\delta z}{\delta x},\dfrac{\delta z}{\delta y}$で表せ.
(1)$x-te^t,y=\log t$
(2)$x=\dfrac{t}{2t+1},y=\dfrac{t+1}{2t+1}$
$z=f(x,y)$:全微分可能である.
$\dfrac{dz}{dt}$を$t,\dfrac{\delta z}{\delta x},\dfrac{\delta z}{\delta y}$で表せ.
(1)$x-te^t,y=\log t$
(2)$x=\dfrac{t}{2t+1},y=\dfrac{t+1}{2t+1}$
投稿日:2021.08.01