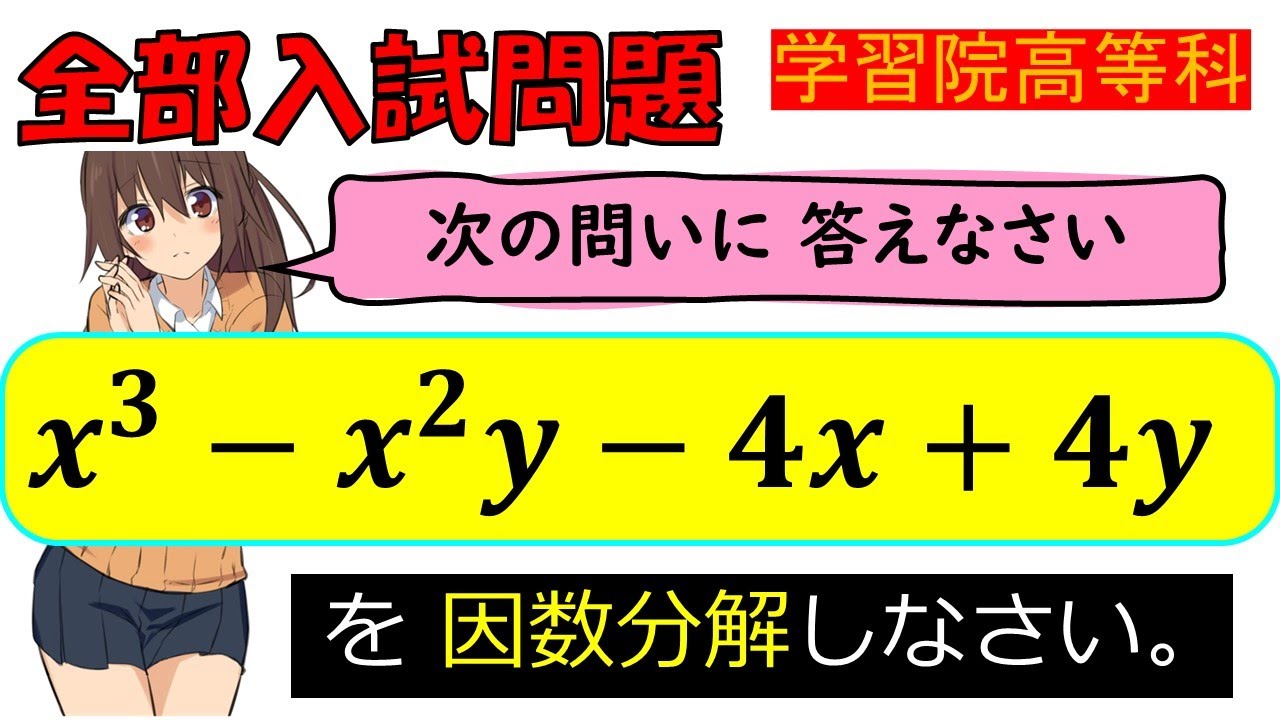
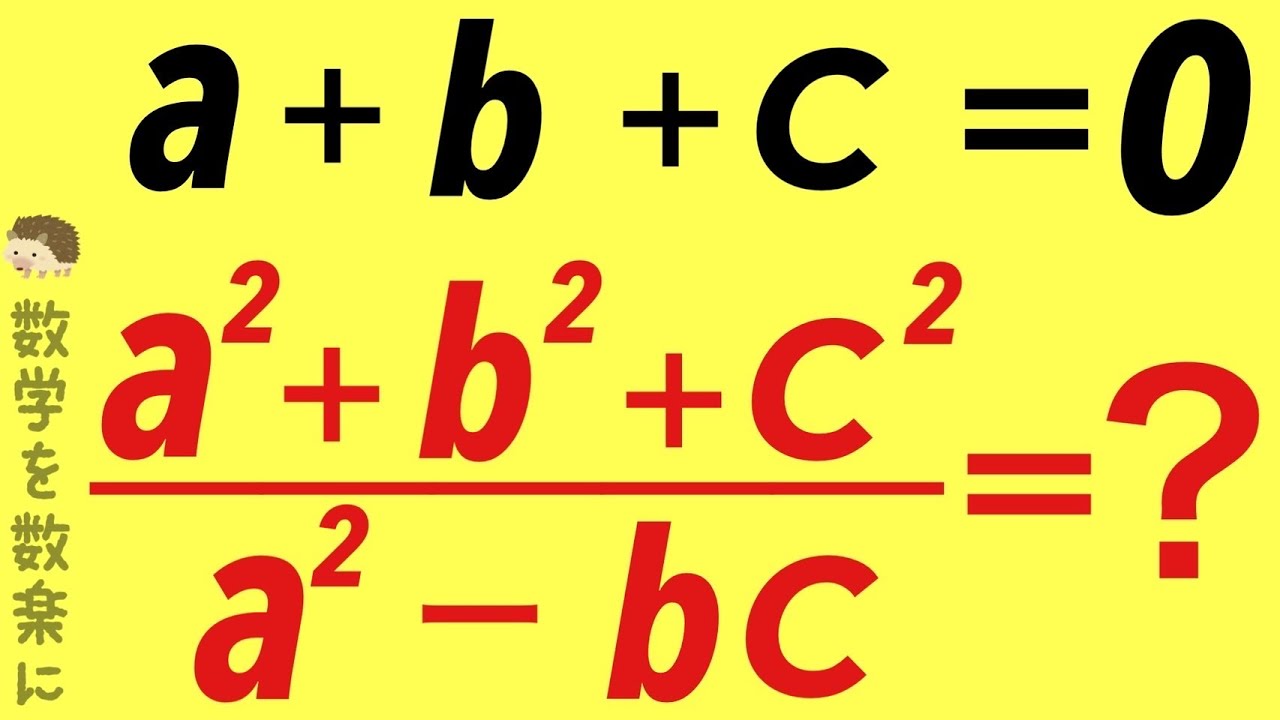問題文全文(内容文):
右の図1で,点$O$は原点,直線$\ell$は関数$y=\dfrac{1}{4}x^2$のグラフを表している.
点$A$,点$B$はともに曲線上にあり,$x$座標はそれぞれ$-4,2$である.
曲線上にある点を$P$とする.このとき,次の各問いに答えよ.
$\boxed{問1}$
点$P$の$y$座標を$a$とする.
点$P$が点$A$から点$B$まで動くとき,
$a$のとる値の範囲を不等号を使って,$\Box \leqq a \leqq \Box$で表せ.
$\boxed{問2}$
右の図2は,図1において,点$P$を通り傾き$-\dfrac{1}{2}$の直線を引き,
$y$軸との交点を$Q$とした場合を表している.
次の①,②に答えよ.
①異なる2点$A,P$を通る直線が$x$軸と平行になるとき,
2点$A,Q$を通る直線の式を求めよ.
②点$P$の$x$座標が2より大きい数であるとき,
点$A$と点$B$,点$A$と点$Q$,点$B$と点$Q$をそれぞれ結んだ場合を考える.
$△ABQ$の面積が30のとき,点$P$の座標を求めよ.
図は動画内を参照
右の図1で,点$O$は原点,直線$\ell$は関数$y=\dfrac{1}{4}x^2$のグラフを表している.
点$A$,点$B$はともに曲線上にあり,$x$座標はそれぞれ$-4,2$である.
曲線上にある点を$P$とする.このとき,次の各問いに答えよ.
$\boxed{問1}$
点$P$の$y$座標を$a$とする.
点$P$が点$A$から点$B$まで動くとき,
$a$のとる値の範囲を不等号を使って,$\Box \leqq a \leqq \Box$で表せ.
$\boxed{問2}$
右の図2は,図1において,点$P$を通り傾き$-\dfrac{1}{2}$の直線を引き,
$y$軸との交点を$Q$とした場合を表している.
次の①,②に答えよ.
①異なる2点$A,P$を通る直線が$x$軸と平行になるとき,
2点$A,Q$を通る直線の式を求めよ.
②点$P$の$x$座標が2より大きい数であるとき,
点$A$と点$B$,点$A$と点$Q$,点$B$と点$Q$をそれぞれ結んだ場合を考える.
$△ABQ$の面積が30のとき,点$P$の座標を求めよ.
図は動画内を参照
単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右の図1で,点$O$は原点,直線$\ell$は関数$y=\dfrac{1}{4}x^2$のグラフを表している.
点$A$,点$B$はともに曲線上にあり,$x$座標はそれぞれ$-4,2$である.
曲線上にある点を$P$とする.このとき,次の各問いに答えよ.
$\boxed{問1}$
点$P$の$y$座標を$a$とする.
点$P$が点$A$から点$B$まで動くとき,
$a$のとる値の範囲を不等号を使って,$\Box \leqq a \leqq \Box$で表せ.
$\boxed{問2}$
右の図2は,図1において,点$P$を通り傾き$-\dfrac{1}{2}$の直線を引き,
$y$軸との交点を$Q$とした場合を表している.
次の①,②に答えよ.
①異なる2点$A,P$を通る直線が$x$軸と平行になるとき,
2点$A,Q$を通る直線の式を求めよ.
②点$P$の$x$座標が2より大きい数であるとき,
点$A$と点$B$,点$A$と点$Q$,点$B$と点$Q$をそれぞれ結んだ場合を考える.
$△ABQ$の面積が30のとき,点$P$の座標を求めよ.
図は動画内を参照
右の図1で,点$O$は原点,直線$\ell$は関数$y=\dfrac{1}{4}x^2$のグラフを表している.
点$A$,点$B$はともに曲線上にあり,$x$座標はそれぞれ$-4,2$である.
曲線上にある点を$P$とする.このとき,次の各問いに答えよ.
$\boxed{問1}$
点$P$の$y$座標を$a$とする.
点$P$が点$A$から点$B$まで動くとき,
$a$のとる値の範囲を不等号を使って,$\Box \leqq a \leqq \Box$で表せ.
$\boxed{問2}$
右の図2は,図1において,点$P$を通り傾き$-\dfrac{1}{2}$の直線を引き,
$y$軸との交点を$Q$とした場合を表している.
次の①,②に答えよ.
①異なる2点$A,P$を通る直線が$x$軸と平行になるとき,
2点$A,Q$を通る直線の式を求めよ.
②点$P$の$x$座標が2より大きい数であるとき,
点$A$と点$B$,点$A$と点$Q$,点$B$と点$Q$をそれぞれ結んだ場合を考える.
$△ABQ$の面積が30のとき,点$P$の座標を求めよ.
図は動画内を参照
投稿日:2016.12.28