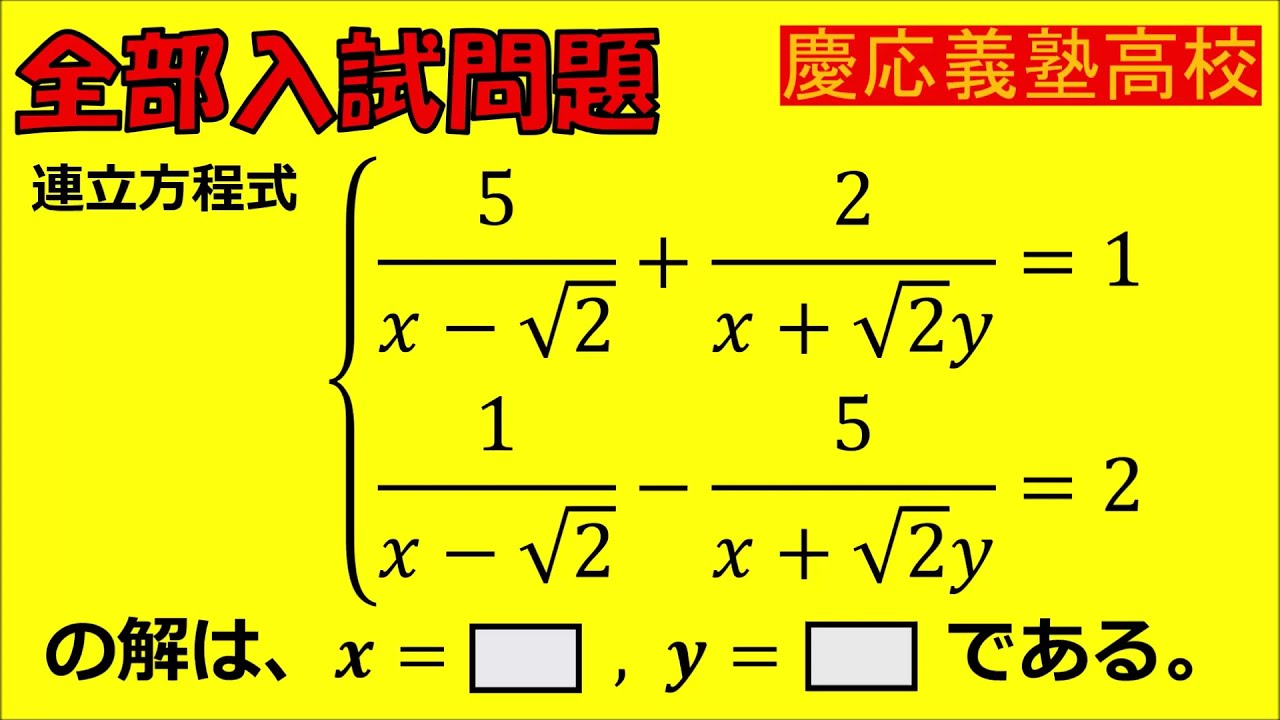
問題文全文(内容文):
①$y=ax^2$について、$ x = 2$のとき$y=-3$である。
このとき、$a$の値を求めなさい。
②$y$は$x$の2乗に比例し、$x=-6$のとき$y = 9$である。
$x = 12$のときの$y$の値を求めなさい。
③右図において、$m$は$y=ax^2$($a$は定数)のグラフで、
$A(3,-4)$は$m$上にある。
このとき、$a$の値を求めなさい。
図は動画内参照
①$y=ax^2$について、$ x = 2$のとき$y=-3$である。
このとき、$a$の値を求めなさい。
②$y$は$x$の2乗に比例し、$x=-6$のとき$y = 9$である。
$x = 12$のときの$y$の値を求めなさい。
③右図において、$m$は$y=ax^2$($a$は定数)のグラフで、
$A(3,-4)$は$m$上にある。
このとき、$a$の値を求めなさい。
図は動画内参照
単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$y=ax^2$について、$ x = 2$のとき$y=-3$である。
このとき、$a$の値を求めなさい。
②$y$は$x$の2乗に比例し、$x=-6$のとき$y = 9$である。
$x = 12$のときの$y$の値を求めなさい。
③右図において、$m$は$y=ax^2$($a$は定数)のグラフで、
$A(3,-4)$は$m$上にある。
このとき、$a$の値を求めなさい。
図は動画内参照
①$y=ax^2$について、$ x = 2$のとき$y=-3$である。
このとき、$a$の値を求めなさい。
②$y$は$x$の2乗に比例し、$x=-6$のとき$y = 9$である。
$x = 12$のときの$y$の値を求めなさい。
③右図において、$m$は$y=ax^2$($a$は定数)のグラフで、
$A(3,-4)$は$m$上にある。
このとき、$a$の値を求めなさい。
図は動画内参照
投稿日:2017.07.04