円と角 女子学院中（改） - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 算数(中学受験) > 平面図形 > 角度と面積 > 円と角　女子学院中（改）

円と角　女子学院中（改）

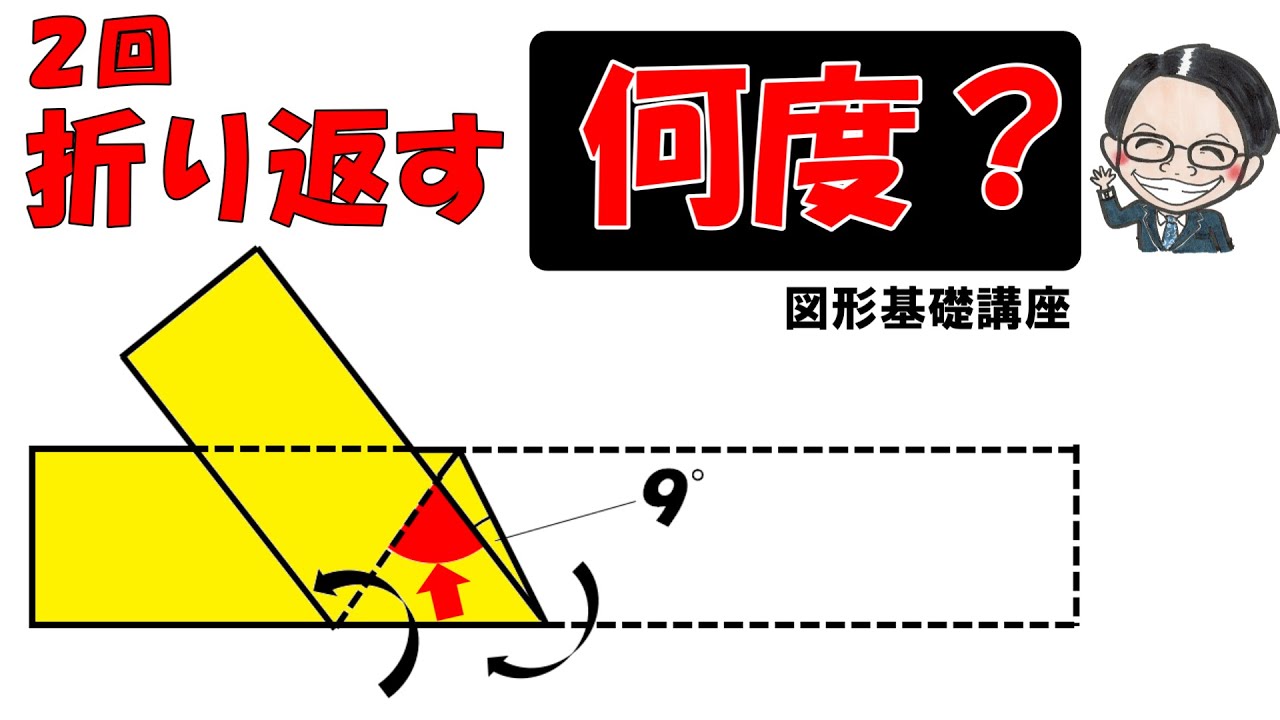
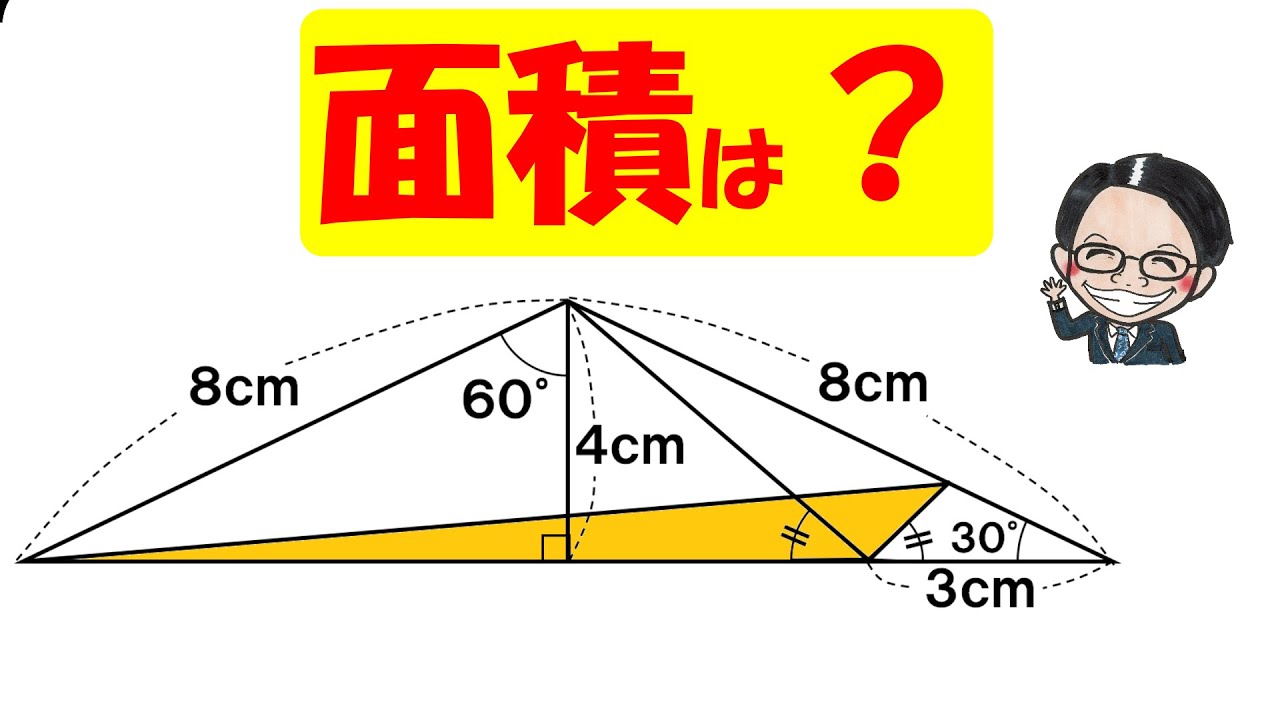
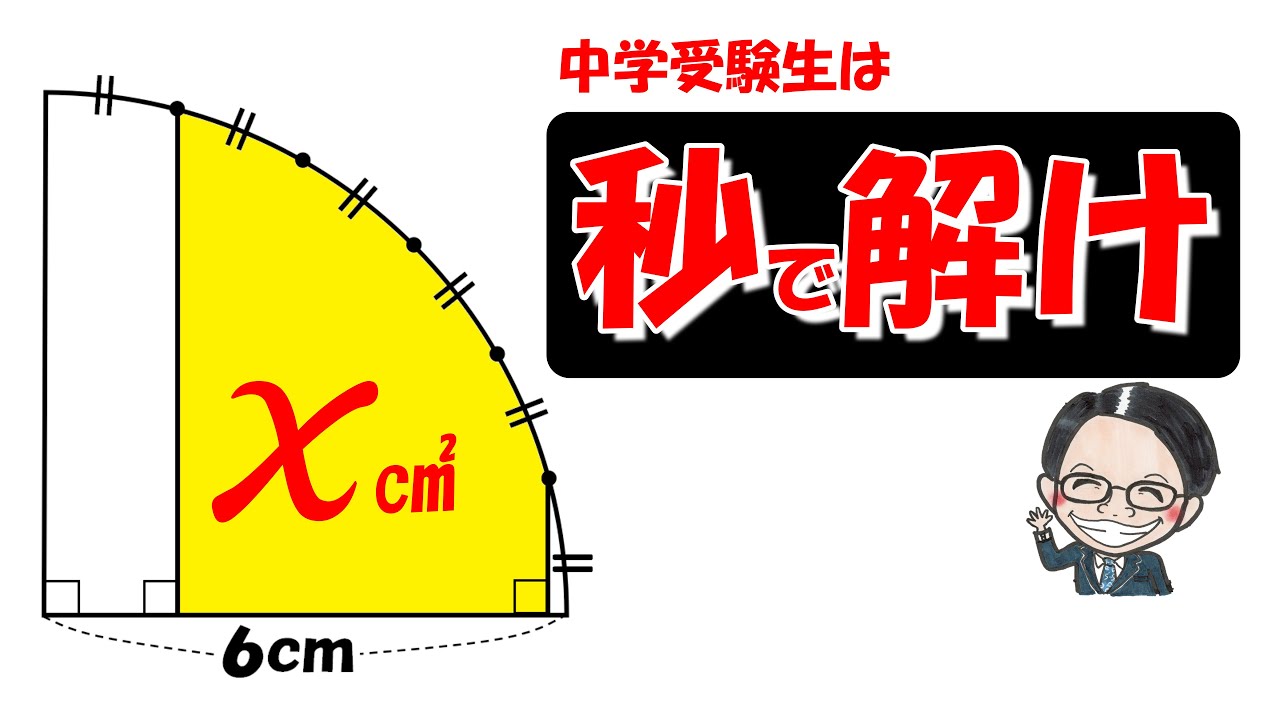
単元： #算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#女子学院中学
指導講師： 数学を数楽に
投稿日：2024.10.04

＜関連動画＞

シンプル過ぎてヤバい鬼難問！解けたらガチ天才！？超初級～最上級まで面白い角度問題５選！【中学受験算数】【入試問題】【難問】

アイキャッチ画像
単元： #算数(中学受験)#平面図形#角度と面積
指導講師： こばちゃん塾
問題文全文(内容文)：
2021中央大学附属中学校
超初級
下図の平行四辺形$\rm{ABCD}$で$\rm{AB}=AE$のとき、$x$は何度？

2021法政大学中学校
初級
下図で$\rm{AB}$と$\rm{CD}$は平行です。$x$は何度？

2021西武学園文理中学校
中級
同じ印のついた角度の大きさが同じであるとき、$x$は何度？

2021早稲田実業中学校
上級
四角形$\rm{ABCD}$は正方形です。
㋐は何度？

S級
下図で$x$は何度？

＊図は動画内参照
この動画を見る　

【フル】マッシュの速さを計算したら意外に遅かった？

アイキャッチ画像
単元： #算数(中学受験)#速さ#速さその他
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
漫画マッシュルの主人公マッシュのビッグバンダッシュの速度に関して解説していきます。
この動画を見る　

解き方は自由だ！　分数式の計算　2024早稲田中

アイキャッチ画像
単元： #算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#早稲田中学
指導講師： 数学を数楽に
問題文全文(内容文)：
以下を解いてください。
$\displaystyle \frac{5}{2\times3}+\displaystyle \frac{11}{3\times4}+\displaystyle \frac{19}{4\times5}+\displaystyle \frac{29}{5\times6}$

出典：2024早稲田中学校　入試問題
この動画を見る　

【小５　算数】　　小５－⑦（旧）　小数のかけ算②

アイキャッチ画像
単元： #算数(中学受験)#計算と数の性質#いろいろな計算
指導講師： とある男が授業をしてみた
問題文全文(内容文)：
小５　算数　小数のかけ算②
次の問に答えよ
\begin{array}{rrrrrrrl}
① & 0.7 & ② & 0.04 & ③ & 3.8 & 　④ & 積が5より大きくなるのは？\\[-3pt]
&
\underline{\times\phantom{0}0.6} &
&
\underline{\times\phantom{0}0.6} &
&
\underline{\times\phantom{0}1.6} &
&
(ア)　5 \times 6\\[-3pt]
&
&
&
&
&
&
&
(イ)　5 \times 2.3\\[-3pt]
&
&
&
&
&
&
&
(ウ)　5 \times 0.98\\[-3pt]
&
&
&
&
&
&
&
(エ)　5 \times 1.02\\[-3pt]
&
&
&
&
&
&
&
(オ)　5 \times 1\\[-3pt]
\end{array}
この動画を見る　

【受験算数】平面図形：転がる図形

アイキャッチ画像
単元： #算数(中学受験)#平面図形#平面図形その他
指導講師： 理数個別チャンネル
問題文全文(内容文)：
三角形ABCが一辺の長さが同じ正方形を滑らないように「あ」から「い」まで転がる。この時のCが動いたあとの長さを求めよ。
この動画を見る　
PAGE TOP