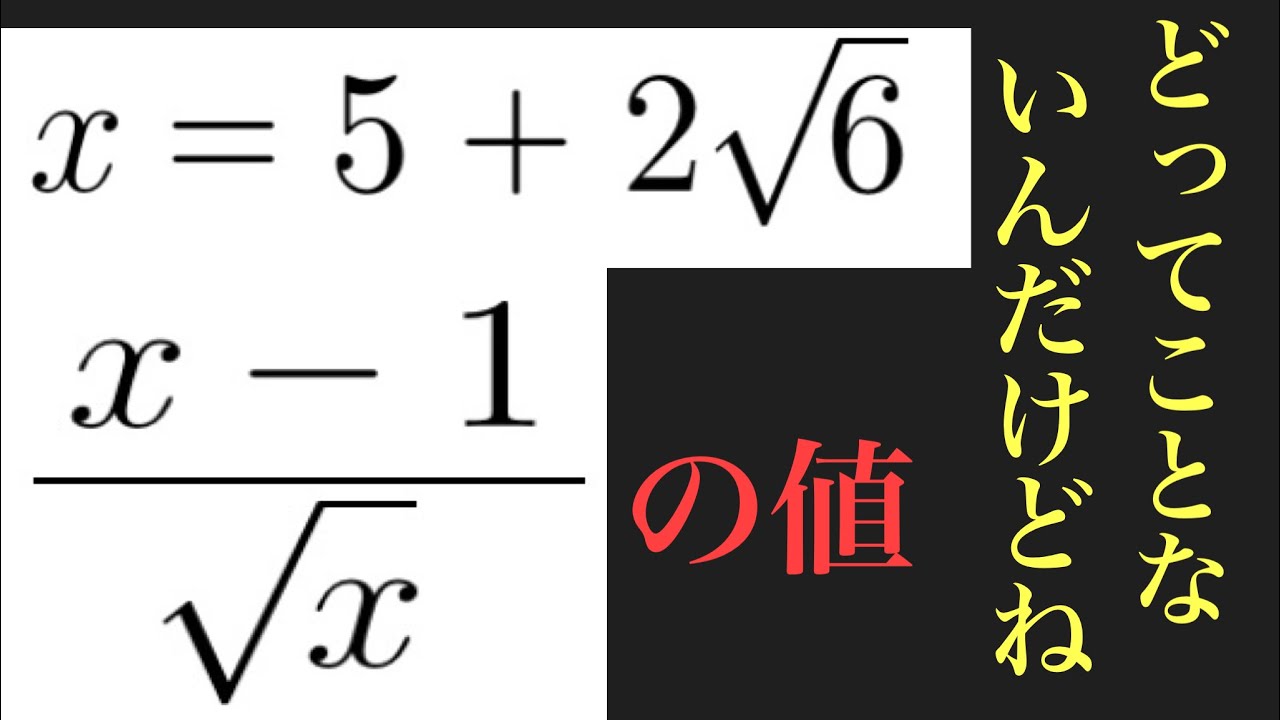【高校数学】数Ⅰ－５５２次方程式② - 質問解決D.B.（データベース）

問題文全文(内容文)：
①$2x^2-5x+1=0$
②$x^2+2x-4=0$
③$\sqrt{ 2 }x^2-4x+2\sqrt{ 2 }=0$
④$(x+2)^2+4(x+2)-1=0$

単元： #数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)

指導講師：とある男が授業をしてみた

問題文全文(内容文)：
①$2x^2-5x+1=0$
②$x^2+2x-4=0$
③$\sqrt{ 2 }x^2-4x+2\sqrt{ 2 }=0$
④$(x+2)^2+4(x+2)-1=0$

投稿日：2014.08.29

単元： #数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)

指導講師：数学を数楽に

問題文全文(内容文)：
緑と青と赤の面積は等しい
AQ=？
＊図は動画内参照

この動画を見る　

単元： #数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
nを自然数とする.
$a_n=19^n+(-1)^{n-1}・3^{6n-5}$
すべての$a_n$を割り切る素数をすべて求めよ.

東工大(類)過去問

この動画を見る　

単元： #数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)

指導講師：数学を数楽に

問題文全文(内容文)：
$x^2+x=5+\sqrt 5$

この動画を見る　

単元： #数Ⅰ#大学入試過去問(数学)#数と式#一次不等式（不等式・絶対値のある方程式・不等式）#センター試験・共通テスト関連#共通テスト#数学(高校生)

指導講師：数学を数楽に

問題文全文(内容文)：
$y=-3x^2$でxの変域が$-4 \leqq x \leqq 1$のとき
$▢ \leqq y \leqq ▢$

2021東京都立共通問題

この動画を見る　

単元： #数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
$ x^3+(x^2-3x+4)^2+2$
これを因数分解せよ.

この動画を見る　