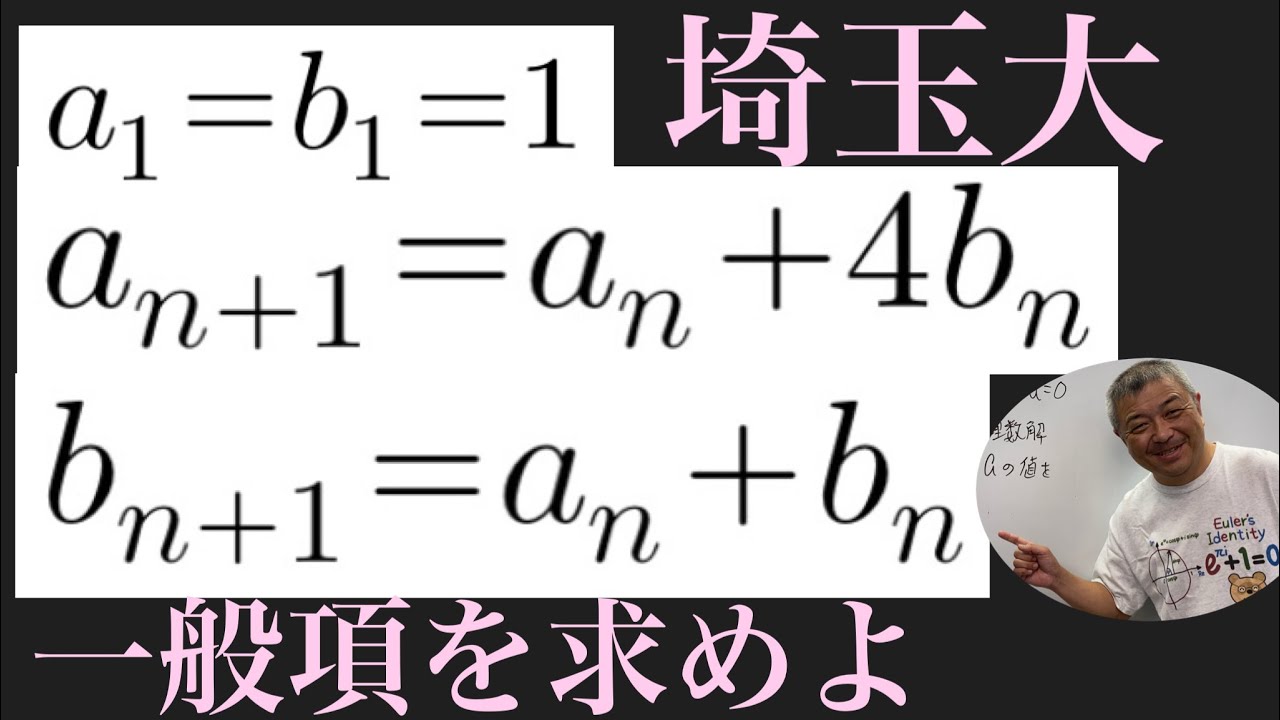【数B】数列：漸化式と数学的帰納法：三項間漸化式 PRIME B 85(1)

【数B】数列：漸化式と数学的帰納法：三項間漸化式　PRIME B 85(1)

問題文全文(内容文)：
次のように定められた数列

a_{n}

の一般項を求めよ。

a_{1} = 1

，

a_{2} = 2

，

a_{n + 2} = 4 a_{n + 1} － 3 a_{n}

チャプター：

0:00 答案には書かない変形！
3:14 ここからを答案に書く！
6:15 二つの変形を整理！
9:51 二つの変形を使ってaₙを求める！

単元： #数列#漸化式#数学(高校生)

教材： #PRIME数学#PRIME数学Ⅱ・B#中高教材

指導講師：理数個別チャンネル

問題文全文(内容文)：
次のように定められた数列

a_{n}

の一般項を求めよ。

a_{1} = 1

，

a_{2} = 2

，

a_{n + 2} = 4 a_{n + 1} － 3 a_{n}

投稿日：2023.09.25

＜関連動画＞

【0から理解できる】数学B 等比数列の和 Σ(シグマ)の計算

単元： #数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B

指導講師：【ゼロから理解できる】高校数学・物理

問題文全文(内容文)：
次の和を求めよ。
（1）

\sum_{k = 1}^{6} 2^{k}

（2）

\sum_{k = 1}^{n} (- 3)^{k}

この動画を見る　

横浜国大　複雑な漸化式

単元： #大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数B

指導講師：鈴木貫太郎

問題文全文(内容文)：

a_{0} = 1

一般項を求めよ

(n

自然数

)

a_{n} = \sum_{k = 1}^{n} 3^{k} a_{n - k}

出典：2000年横浜国立大学　過去問

この動画を見る　

福田の数学〜整数部分の評価が難しい問題〜北里大学2023年医学部第1問(3)〜漸化式と整数部分の評価

単元： #数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#漸化式#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)#数B

指導講師：福田次郎

問題文全文(内容文)：

a = 3 + \sqrt{10}, b = 3 - \sqrt{10}

とし、正の整数nに対して

A_{n} = a^{n} + b^{n}

とおく。
このとき、

A_{2}, A_{3}

の値はそれぞれ

A_{2} = ク, A_{3} = ケ

であり、

A_{n + 2}

を

A_{n + 1}, A_{n}

を用いて表すと

A_{n + 2} = コ

である。
また、

a^{111}

の整数部分を

k

とするとき、kを10で割ると

サ

余る。

2023北里大学医過去問

この動画を見る　

愛媛大　解けないタイプの漸化式

単元： #数列#愛媛大学

指導講師：鈴木貫太郎

問題文全文(内容文)：
2023愛媛大学過去問題

a_{1} = 2

a_{n + 1} = a_{n}^{2} + 2 (n = 1, 2, 3, \dots)

mが自然数なら

a_{2 m}

は6の倍数であることを示せ

この動画を見る　

東北大文系　虚数のナイスな問題

単元： #数Ⅱ#大学入試過去問(数学)#複素数と方程式#解と判別式・解と係数の関係#数列#漸化式#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数B

指導講師：鈴木貫太郎

問題文全文(内容文)：
pは0でない実数である.

x^{2} - p x + 5 p = 0

の解を

α, β

とする.
(1)

α^{5} + β^{5} = p \5

となるpを求めよ.
(2)

α

は虚数で

α^{5}

が実数となるpを求めよ.

東北大文系過去問

この動画を見る　

<img src="https://kaiketsu-db.net/wp-content/uploads/2021/11/112-book-morph-outline.gif" alt="" data-eio="l"> 【数B】数列：漸化式と数学的帰納法：三項間漸化式 PRIME B 85(1)

＜関連動画＞

【0から理解できる】数学B 等比数列の和 Σ(シグマ)の計算

横浜国大 複雑な漸化式

福田の数学〜整数部分の評価が難しい問題〜北里大学2023年医学部第1問(3)〜漸化式と整数部分の評価

愛媛大 解けないタイプの漸化式

東北大文系 虚数のナイスな問題