問題文全文(内容文):
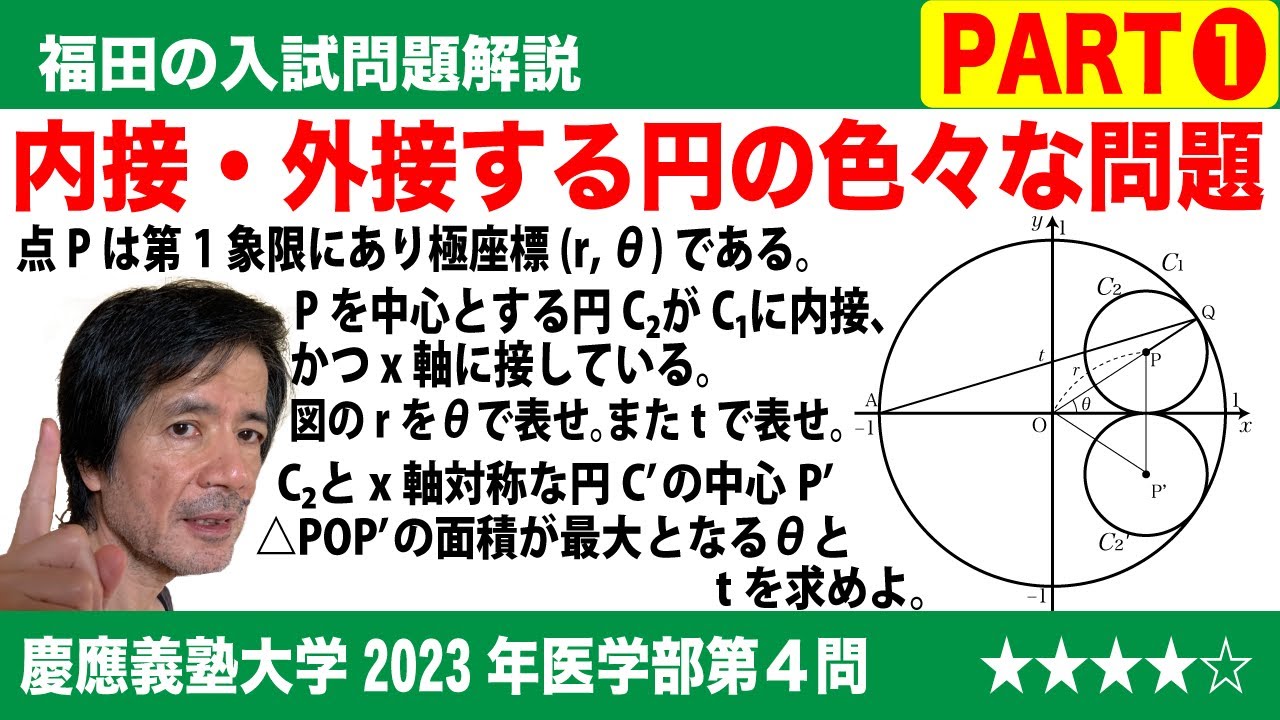
$\Large\boxed{6}$ $i$を虚数単位とする。複素数平面に関する以下の問いに答えよ。
(1)等式|$z$+2|=2|$z$-1| を満たす点$z$の全体が表す図形は円であることを示し、その中心と半径を求めよ。
(2)等式
$\left\{|z+2|-2|z-1|\right\}$$|z+6i|$=$3\left\{|z+2|-2|z-1|\right\}$$|z-2i|$
を満たす点$z$の全体が表す図形をSとする。このときSを複素数平面上に図示せよ。
(3)点$z$が(2)における図形S上を動くとき、$w$=$\frac{1}{z}$ で定義される点$w$が描く図形を複素数平面上に図示せよ。
2023筑波大学理系過去問
$\Large\boxed{6}$ $i$を虚数単位とする。複素数平面に関する以下の問いに答えよ。
(1)等式|$z$+2|=2|$z$-1| を満たす点$z$の全体が表す図形は円であることを示し、その中心と半径を求めよ。
(2)等式
$\left\{|z+2|-2|z-1|\right\}$$|z+6i|$=$3\left\{|z+2|-2|z-1|\right\}$$|z-2i|$
を満たす点$z$の全体が表す図形をSとする。このときSを複素数平面上に図示せよ。
(3)点$z$が(2)における図形S上を動くとき、$w$=$\frac{1}{z}$ で定義される点$w$が描く図形を複素数平面上に図示せよ。
2023筑波大学理系過去問
単元:
#数Ⅱ#大学入試過去問(数学)#複素数平面#図形と方程式#軌跡と領域#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{6}$ $i$を虚数単位とする。複素数平面に関する以下の問いに答えよ。
(1)等式|$z$+2|=2|$z$-1| を満たす点$z$の全体が表す図形は円であることを示し、その中心と半径を求めよ。
(2)等式
$\left\{|z+2|-2|z-1|\right\}$$|z+6i|$=$3\left\{|z+2|-2|z-1|\right\}$$|z-2i|$
を満たす点$z$の全体が表す図形をSとする。このときSを複素数平面上に図示せよ。
(3)点$z$が(2)における図形S上を動くとき、$w$=$\frac{1}{z}$ で定義される点$w$が描く図形を複素数平面上に図示せよ。
2023筑波大学理系過去問
$\Large\boxed{6}$ $i$を虚数単位とする。複素数平面に関する以下の問いに答えよ。
(1)等式|$z$+2|=2|$z$-1| を満たす点$z$の全体が表す図形は円であることを示し、その中心と半径を求めよ。
(2)等式
$\left\{|z+2|-2|z-1|\right\}$$|z+6i|$=$3\left\{|z+2|-2|z-1|\right\}$$|z-2i|$
を満たす点$z$の全体が表す図形をSとする。このときSを複素数平面上に図示せよ。
(3)点$z$が(2)における図形S上を動くとき、$w$=$\frac{1}{z}$ で定義される点$w$が描く図形を複素数平面上に図示せよ。
2023筑波大学理系過去問
投稿日:2023.07.03