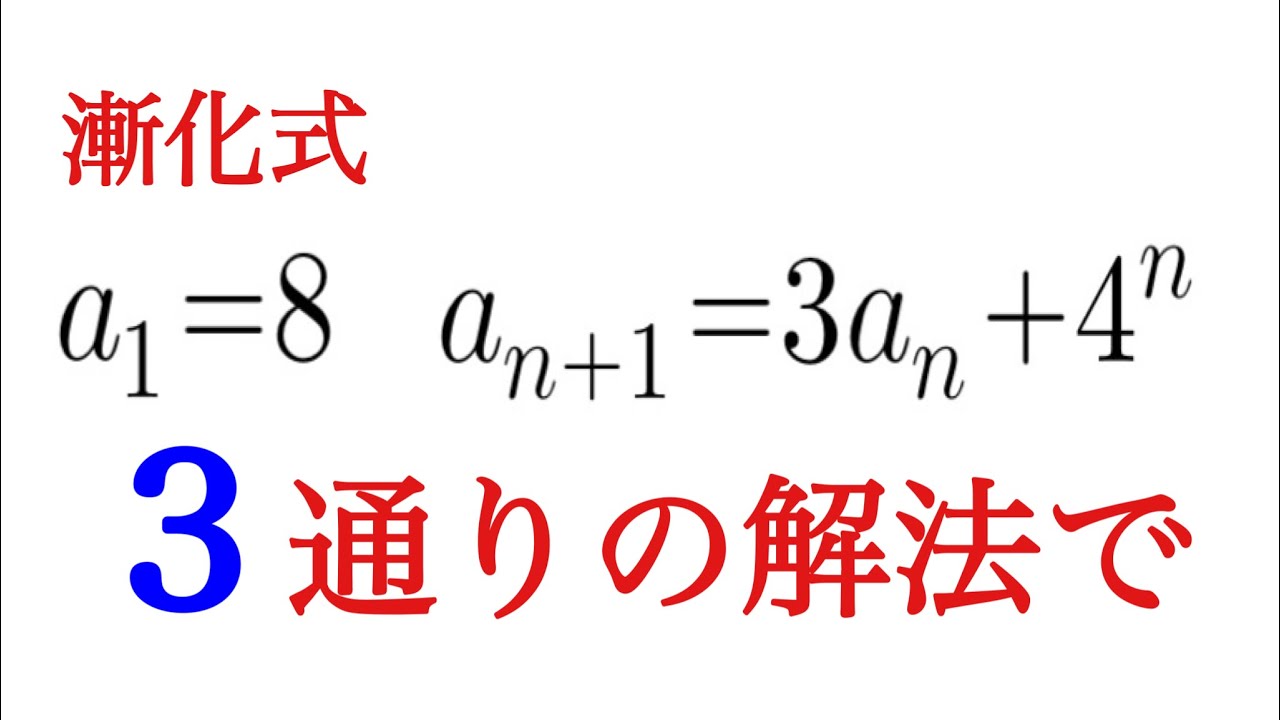数学「大学入試良問集」【13−5 漸化式（割り算型）】を宇宙一わかりやすく - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(高校生) > 数B > 数列 > 漸化式 > 数学「大学入試良問集」【13−5 漸化式（割り算型）】を宇宙一わかりやすく

数学「大学入試良問集」【13−5 漸化式（割り算型）】を宇宙一わかりやすく

問題文全文(内容文)：
数列$\{a_n\}$は
$a_1=9,a_{n+1}=4a_n+5^n(n=1,2,・・・)$をみたす。このとき、次の問いに答えよ。

（1）$b_n=a_n-5^n$とおく。$b_{n+1}$を$b_n$で表せ。
（2）数列$\{a_n\}$の一般項を求めよ。
単元： #大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数B
指導講師： ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文)：
数列$\{a_n\}$は
$a_1=9,a_{n+1}=4a_n+5^n(n=1,2,・・・)$をみたす。このとき、次の問いに答えよ。

（1）$b_n=a_n-5^n$とおく。$b_{n+1}$を$b_n$で表せ。
（2）数列$\{a_n\}$の一般項を求めよ。
投稿日：2021.05.31

＜関連動画＞

17東京都教員採用試験（数学：1-7番　シグマと極限値）

アイキャッチ画像
単元： #数列#数列とその和（等差・等比・階差・Σ）#関数と極限#数列の極限#その他#数学(高校生)#数B#数Ⅲ#教員採用試験
指導講師： ますただ
問題文全文(内容文)：
1⃣-(7)
$\displaystyle \lim_{ n \to \infty } \frac{2(1+2^2+3^2+\cdots+n^2)^4}{(1+2^5+3^5+\cdots+n^5)^2}$
この動画を見る　

連立漸化式

アイキャッチ画像
単元： #数列#漸化式#数学(高校生)#数B
指導講師： 鈴木貫太郎
問題文全文(内容文)：
$a_1=b_1=1$
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_{n+1}=7a_n+6b_n+4 \\
b_{n+1}=-4a_n-3b_n-2
\end{array}
\right.
\end{eqnarray}$
この動画を見る　

福田の数学〜誘導付き3項間の漸化式を解く〜明治大学2023年全学部統一ⅠⅡＡＢ第1問(1)〜３項間漸化式の解法

アイキャッチ画像
単元： #大学入試過去問(数学)#数列#数列とその和（等差・等比・階差・Σ）#漸化式#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数B
指導講師： 福田次郎
問題文全文(内容文)：
$a_{n+2}=4(a_{n+1}-a_n)$$(n=1,2,3,...)$
$a_1=2,a_2=16$
(1)$b_n=a_{n+1}-2a_n$$(n=1,2,3,...)$と置いて$b_n$を求めよ。
(2)$a_n$を求めよ。

2023明治大学全統過去問
この動画を見る　

数検準1級2次過去問【2020年12月】2番：数列

アイキャッチ画像
単元： #数学検定・数学甲子園・数学オリンピック等#数列#数列とその和（等差・等比・階差・Σ）#数学検定#数学検定準1級#数学(高校生)#数B
指導講師： ますただ
問題文全文(内容文)：
$\boxed{2}$ $a_1=10,a_{n+1}=\sqrt[5]{a_n}$である.

(1)一般項$a_n$を求めよ.
(2)$P_n=a_1 \times \cdots \times a_n$を求めよ.
この動画を見る　

【高校数学】　数B－６８　等比数列とその和④

アイキャッチ画像
単元： #数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師： とある男が授業をしてみた
問題文全文(内容文)：
初項$a$,公比$r$,項数$n$の等比数列の和を$S_n$とすると
$r \neq 1$のとき,$S_n=①=②$
$r=1$のとき,$S_n=③$

次の等比数列の初項から第$n$項までの和と第5項までの和を求めよう.

④$1,3,9,･･･$

⑤$-2,-2,-2,･･･$

⑥$-1,2,-4,･･･$
この動画を見る　
PAGE TOP