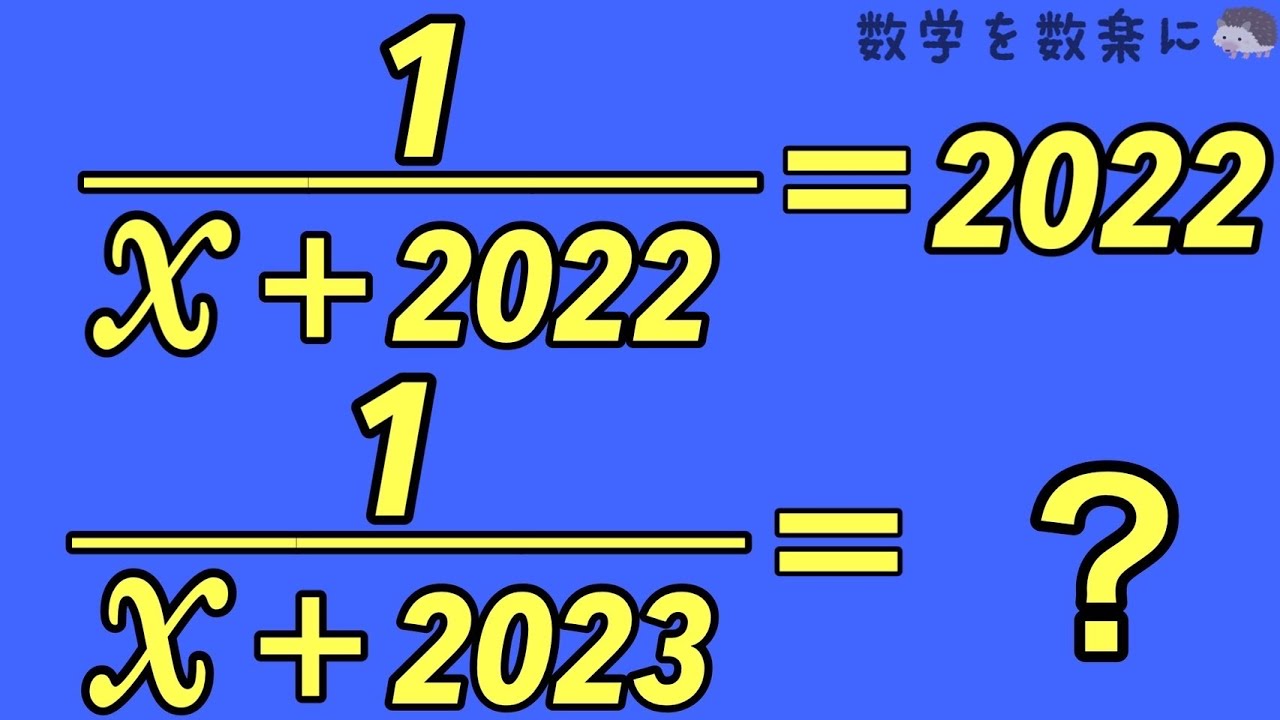問題文全文(内容文):
入試問題 久留米大附設高等学校
次の計算をせよ。
$\{(\displaystyle \frac{\sqrt{ 3 }}{\sqrt{ 2 }+1} ) ^2+ (\displaystyle \frac{\sqrt{ 3 }}{\sqrt{ 2 }-1} )^2\}^2-\{(\displaystyle \frac{\sqrt{ 3 }}{\sqrt{ 2 }+1} )^2 - (\displaystyle \frac{\sqrt{ 3 }}{\sqrt{ 2 }-1} )^2\}^2$
入試問題 久留米大附設高等学校
次の計算をせよ。
$\{(\displaystyle \frac{\sqrt{ 3 }}{\sqrt{ 2 }+1} ) ^2+ (\displaystyle \frac{\sqrt{ 3 }}{\sqrt{ 2 }-1} )^2\}^2-\{(\displaystyle \frac{\sqrt{ 3 }}{\sqrt{ 2 }+1} )^2 - (\displaystyle \frac{\sqrt{ 3 }}{\sqrt{ 2 }-1} )^2\}^2$
単元:
#中3数学#高校入試過去問(数学)#久留米大学附設高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 久留米大附設高等学校
次の計算をせよ。
$\{(\displaystyle \frac{\sqrt{ 3 }}{\sqrt{ 2 }+1} ) ^2+ (\displaystyle \frac{\sqrt{ 3 }}{\sqrt{ 2 }-1} )^2\}^2-\{(\displaystyle \frac{\sqrt{ 3 }}{\sqrt{ 2 }+1} )^2 - (\displaystyle \frac{\sqrt{ 3 }}{\sqrt{ 2 }-1} )^2\}^2$
入試問題 久留米大附設高等学校
次の計算をせよ。
$\{(\displaystyle \frac{\sqrt{ 3 }}{\sqrt{ 2 }+1} ) ^2+ (\displaystyle \frac{\sqrt{ 3 }}{\sqrt{ 2 }-1} )^2\}^2-\{(\displaystyle \frac{\sqrt{ 3 }}{\sqrt{ 2 }+1} )^2 - (\displaystyle \frac{\sqrt{ 3 }}{\sqrt{ 2 }-1} )^2\}^2$
投稿日:2021.05.02