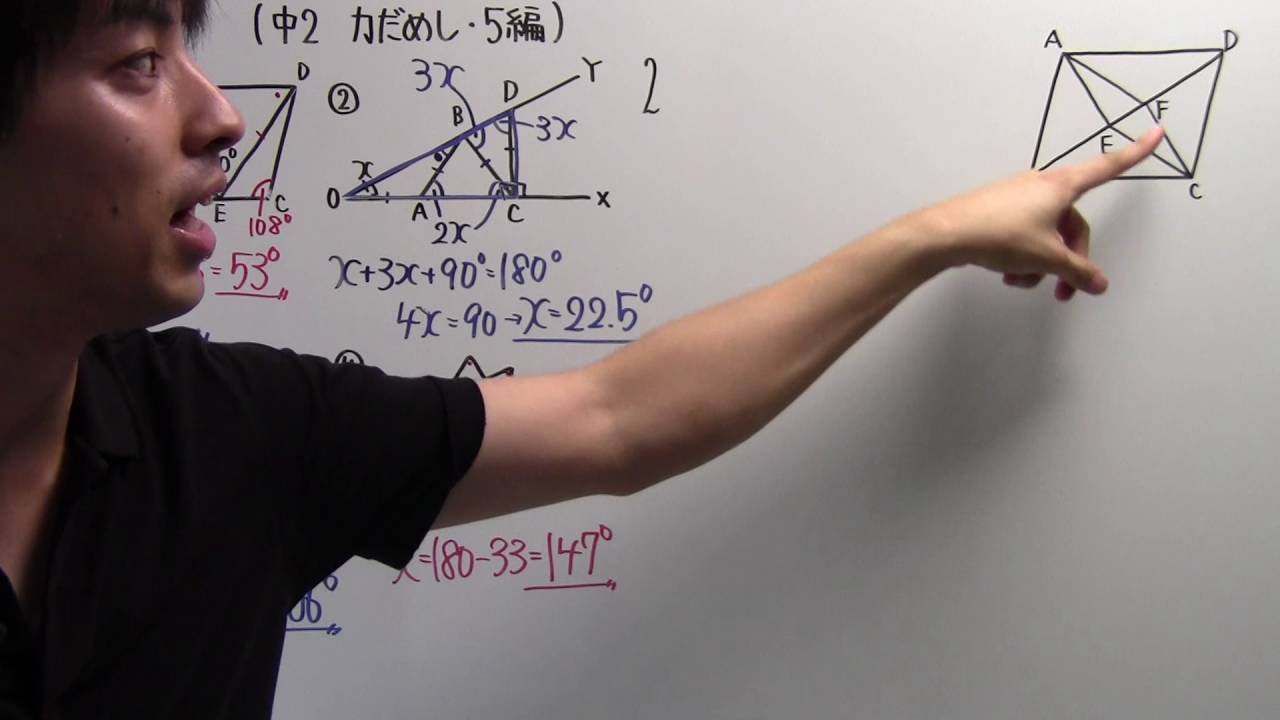問題文全文(内容文):
問題5.右の図のように、平行四辺形ABCDの対角線AC上にAE=EF=FCとなるように、点E、Fを点Aに近いほうからこの
順にとり、点BとE、点DとFをそれぞれ線分で結びます。このとき、BE=DFとなることは、下のように証明できます。
[証明]
△ABEと△CDFにおいて
仮定より、AE=CF …①
[ア]から、AB=CD …②
AB∥DCより、[イ]から、∠BAE=∠DCF …③
①、②、③より、[ウ]から、△ABE≡△CDF
合同な図形の対応する辺は等しいから、BE=DF
次の問いに答えなさい。
(10) [ア]、[イ]にあてはまる言葉を、下のあ~おの中からそれぞれ1つ選びなさい。
あ 平行四辺形の向かい合う辺は等しい
い 平行四辺形の向かい合う角は等しい
う 平行四辺形の対角線はそれぞれの中点で交わる
え 平行線の同位角は等しい
お 平行線の錯角は等しい
(11) [ウ]にあてはまる合同条件を、下のか~この中から1つ選びなさい。
か 3組の辺がそれぞれ等しい
き 2組の辺とその間の角がそれぞれ等しい。
く 1組の辺とその両端の角がそれぞれ等しい。
け 直角三角形の斜辺と1つの鋭角がそれぞれ等しい。
こ 直角三角形の斜辺と他の1辺がそれぞれ等しい。
(12) △ABEの面積が12㎝²であるとき、△ACDの面積は何㎝²ですか。
単位をつけて答えなさい。
問題5.右の図のように、平行四辺形ABCDの対角線AC上にAE=EF=FCとなるように、点E、Fを点Aに近いほうからこの
順にとり、点BとE、点DとFをそれぞれ線分で結びます。このとき、BE=DFとなることは、下のように証明できます。
[証明]
△ABEと△CDFにおいて
仮定より、AE=CF …①
[ア]から、AB=CD …②
AB∥DCより、[イ]から、∠BAE=∠DCF …③
①、②、③より、[ウ]から、△ABE≡△CDF
合同な図形の対応する辺は等しいから、BE=DF
次の問いに答えなさい。
(10) [ア]、[イ]にあてはまる言葉を、下のあ~おの中からそれぞれ1つ選びなさい。
あ 平行四辺形の向かい合う辺は等しい
い 平行四辺形の向かい合う角は等しい
う 平行四辺形の対角線はそれぞれの中点で交わる
え 平行線の同位角は等しい
お 平行線の錯角は等しい
(11) [ウ]にあてはまる合同条件を、下のか~この中から1つ選びなさい。
か 3組の辺がそれぞれ等しい
き 2組の辺とその間の角がそれぞれ等しい。
く 1組の辺とその両端の角がそれぞれ等しい。
け 直角三角形の斜辺と1つの鋭角がそれぞれ等しい。
こ 直角三角形の斜辺と他の1辺がそれぞれ等しい。
(12) △ABEの面積が12㎝²であるとき、△ACDの面積は何㎝²ですか。
単位をつけて答えなさい。
チャプター:
0:00 問題説明
1:05 (10)の解説
2:56 (11)の解説
3:44 (12)の解説
5:39 まとめ
単元:
#数学(中学生)#中2数学#数学検定・数学甲子園・数学オリンピック等#平行と合同#三角形と四角形#数学検定#数学検定3級
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題5.右の図のように、平行四辺形ABCDの対角線AC上にAE=EF=FCとなるように、点E、Fを点Aに近いほうからこの
順にとり、点BとE、点DとFをそれぞれ線分で結びます。このとき、BE=DFとなることは、下のように証明できます。
[証明]
△ABEと△CDFにおいて
仮定より、AE=CF …①
[ア]から、AB=CD …②
AB∥DCより、[イ]から、∠BAE=∠DCF …③
①、②、③より、[ウ]から、△ABE≡△CDF
合同な図形の対応する辺は等しいから、BE=DF
次の問いに答えなさい。
(10) [ア]、[イ]にあてはまる言葉を、下のあ~おの中からそれぞれ1つ選びなさい。
あ 平行四辺形の向かい合う辺は等しい
い 平行四辺形の向かい合う角は等しい
う 平行四辺形の対角線はそれぞれの中点で交わる
え 平行線の同位角は等しい
お 平行線の錯角は等しい
(11) [ウ]にあてはまる合同条件を、下のか~この中から1つ選びなさい。
か 3組の辺がそれぞれ等しい
き 2組の辺とその間の角がそれぞれ等しい。
く 1組の辺とその両端の角がそれぞれ等しい。
け 直角三角形の斜辺と1つの鋭角がそれぞれ等しい。
こ 直角三角形の斜辺と他の1辺がそれぞれ等しい。
(12) △ABEの面積が12㎝²であるとき、△ACDの面積は何㎝²ですか。
単位をつけて答えなさい。
問題5.右の図のように、平行四辺形ABCDの対角線AC上にAE=EF=FCとなるように、点E、Fを点Aに近いほうからこの
順にとり、点BとE、点DとFをそれぞれ線分で結びます。このとき、BE=DFとなることは、下のように証明できます。
[証明]
△ABEと△CDFにおいて
仮定より、AE=CF …①
[ア]から、AB=CD …②
AB∥DCより、[イ]から、∠BAE=∠DCF …③
①、②、③より、[ウ]から、△ABE≡△CDF
合同な図形の対応する辺は等しいから、BE=DF
次の問いに答えなさい。
(10) [ア]、[イ]にあてはまる言葉を、下のあ~おの中からそれぞれ1つ選びなさい。
あ 平行四辺形の向かい合う辺は等しい
い 平行四辺形の向かい合う角は等しい
う 平行四辺形の対角線はそれぞれの中点で交わる
え 平行線の同位角は等しい
お 平行線の錯角は等しい
(11) [ウ]にあてはまる合同条件を、下のか~この中から1つ選びなさい。
か 3組の辺がそれぞれ等しい
き 2組の辺とその間の角がそれぞれ等しい。
く 1組の辺とその両端の角がそれぞれ等しい。
け 直角三角形の斜辺と1つの鋭角がそれぞれ等しい。
こ 直角三角形の斜辺と他の1辺がそれぞれ等しい。
(12) △ABEの面積が12㎝²であるとき、△ACDの面積は何㎝²ですか。
単位をつけて答えなさい。
投稿日:2022.10.01