【中学数学】数学用語チェック絵本 act2 vol.5 三角形と四角形 1

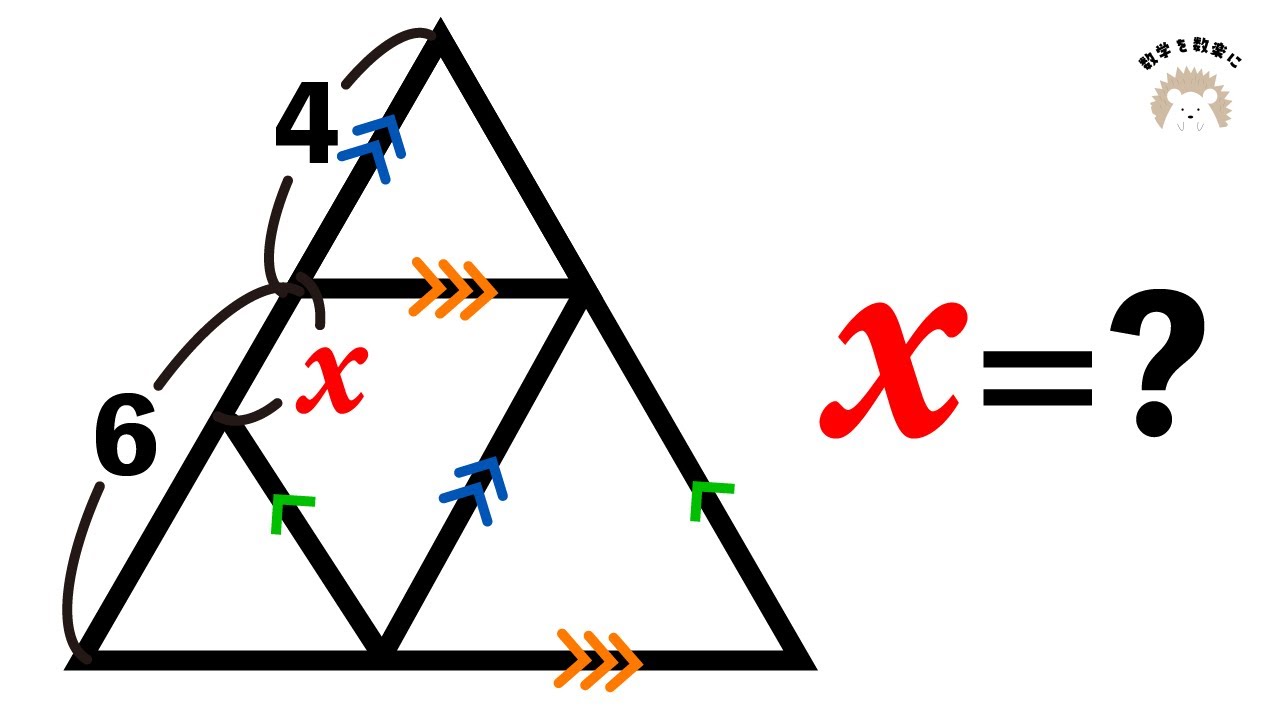
問題文全文(内容文)：
三角形と四角形の用語をチェック！覚えることが多いけど、頑張ろう！

チャプター：

0:00 オープニング
0:07 本編
2:07 キャラクター紹介
2:20 エンディング

単元： #数学(中学生)#中２数学#三角形と四角形

指導講師：理数個別チャンネル

問題文全文(内容文)：
三角形と四角形の用語をチェック！覚えることが多いけど、頑張ろう！

投稿日：2023.06.09

単元： #数学(中学生)#中２数学#平行と合同#相似な図形#三角形と四角形

指導講師：数学を数楽に

問題文全文(内容文)：
動画の四角形において、その中にある$\triangle \rm{CDE}$を求めよ。

この動画を見る　

単元： #数学(中学生)#中２数学#三角形と四角形#高校入試過去問(数学)

指導講師：数学を数楽に

問題文全文(内容文)：
a=?
＊図は動画内参照

大阪星光学院高等学校

この動画を見る　

単元： #数学(中学生)#中２数学#式の計算（単項式・多項式・式の四則計算）

指導講師：数学を数楽に

問題文全文(内容文)：
$16 \times 25 \times 25 =$

この動画を見る　

単元： #数学(中学生)#中２数学#確率#高校入試過去問(数学)#法政大学高等学校

指導講師：高校入試から見た数学の世界「全部入試問題」by しろたん

問題文全文(内容文)：
入試問題　法政大学高等学校

点Aから書き始めて一筆書きする方法は
全部で何通りあるか求めよ。
※図は動画内参照

この動画を見る　

単元： #数学(中学生)#中２数学#1次関数

指導講師：理数個別チャンネル

問題文全文(内容文)：
次の条件を満たす1次関数を求めよ。直線y=2x-4に平行で、直線y=-2x+4とy軸上で交わる

この動画を見る　