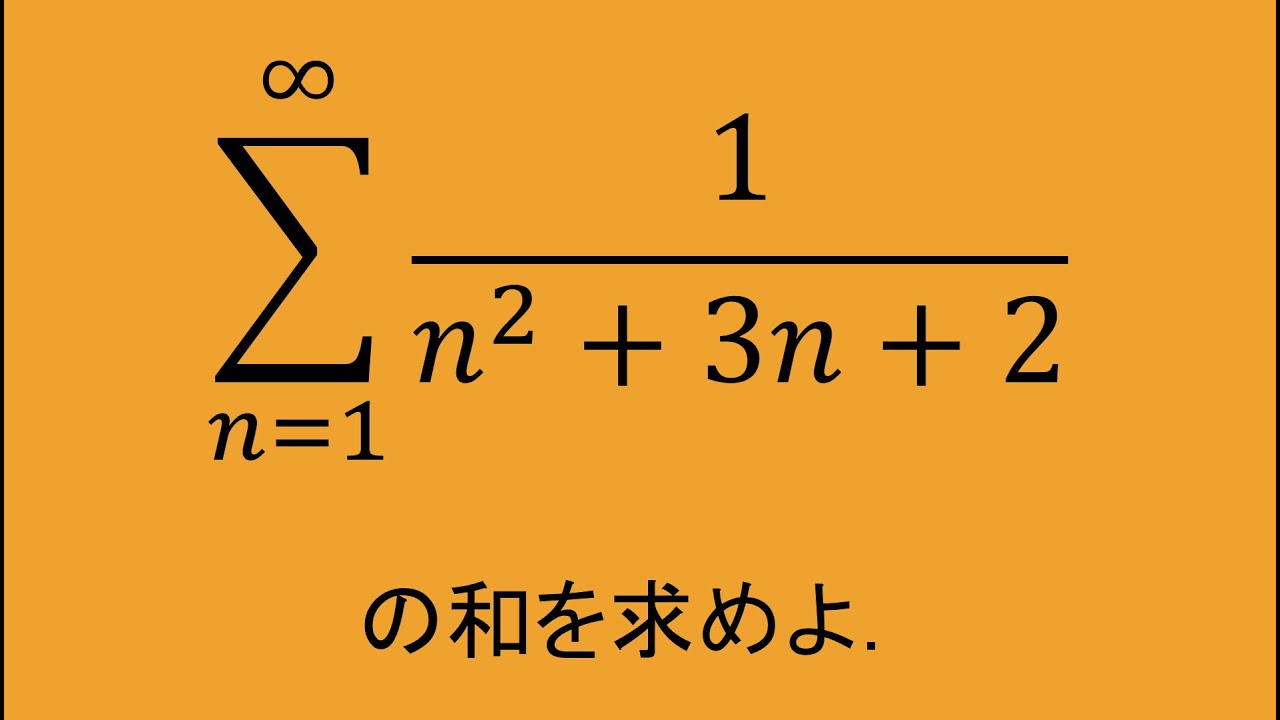例のアレ - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(高校生) > 数B > 数列 > 数列とその和（等差・等比・階差・Σ） > 例のアレ

例のアレ

問題文全文(内容文)：
$\displaystyle \frac{1}{1×2×3×4}＋\displaystyle \frac{1}{2×3×4×5}+\displaystyle \frac{1}{3×4×5×6}$$＋…+\displaystyle \frac{1}{6×7×8×9}＋\displaystyle \frac{1}{7×8×9×10}$
単元： #数列とその和（等差・等比・階差・Σ）
指導講師： 鈴木貫太郎
問題文全文(内容文)：
$\displaystyle \frac{1}{1×2×3×4}＋\displaystyle \frac{1}{2×3×4×5}+\displaystyle \frac{1}{3×4×5×6}$$＋…+\displaystyle \frac{1}{6×7×8×9}＋\displaystyle \frac{1}{7×8×9×10}$
投稿日：2023.12.05

＜関連動画＞

百マス計算全部出したらなんぼ？

アイキャッチ画像
単元： #数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
「百マス計算全部出したらいくつか」について解説しています。
この動画を見る　

【高校数学】　数B－５７　等差数列とその和①

アイキャッチ画像
単元： #数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師： とある男が授業をしてみた
問題文全文(内容文)：
各項に一定の数$d$を加えると,次の項が得られるとき,
この数列といい,$d$を①という.
このとき,すべての自然数$n$について,②$a_n+1=\quad $が成り立つ.
また,初項$a$,公差$d$の等差数列$\{a_n\}$の一般項は③$a_n=\quad $で
求めることができる.

次の等差数列の$\Box$に適する数を入れ,一般項を求めよ.

④$3,5,7,\Box,･･･$

⑤$\Box,11,8,5,･･･$

⑥$11,\Box,25,･･･$
この動画を見る　

【高校数学】数列の和と一般項～理解して覚えようね～ 3-10【数学Ｂ】

アイキャッチ画像
単元： #数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
数列の和と一般項の関係について解説しています。
この動画を見る　

日本医科大学　三次方程式の解が等比数列

アイキャッチ画像
単元： #数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師： 鈴木貫太郎
問題文全文(内容文)：
$p,q$は実数である.
$x^3+6x^2-px-q=0$は3つの実数解である.
$4,\alpha,\beta$をもち,3解の順番を適当に入れかえると等比数列になる$p,q,\alpha,\beta$を求めよ.

2018日本医科大過去問
この動画を見る　

【高校数学】等差数列の和の公式～理解したら簡単です～ 3-4【数学Ｂ】

アイキャッチ画像
単元： #数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
等差数列の和の公式 解説動画です
この動画を見る　
PAGE TOP