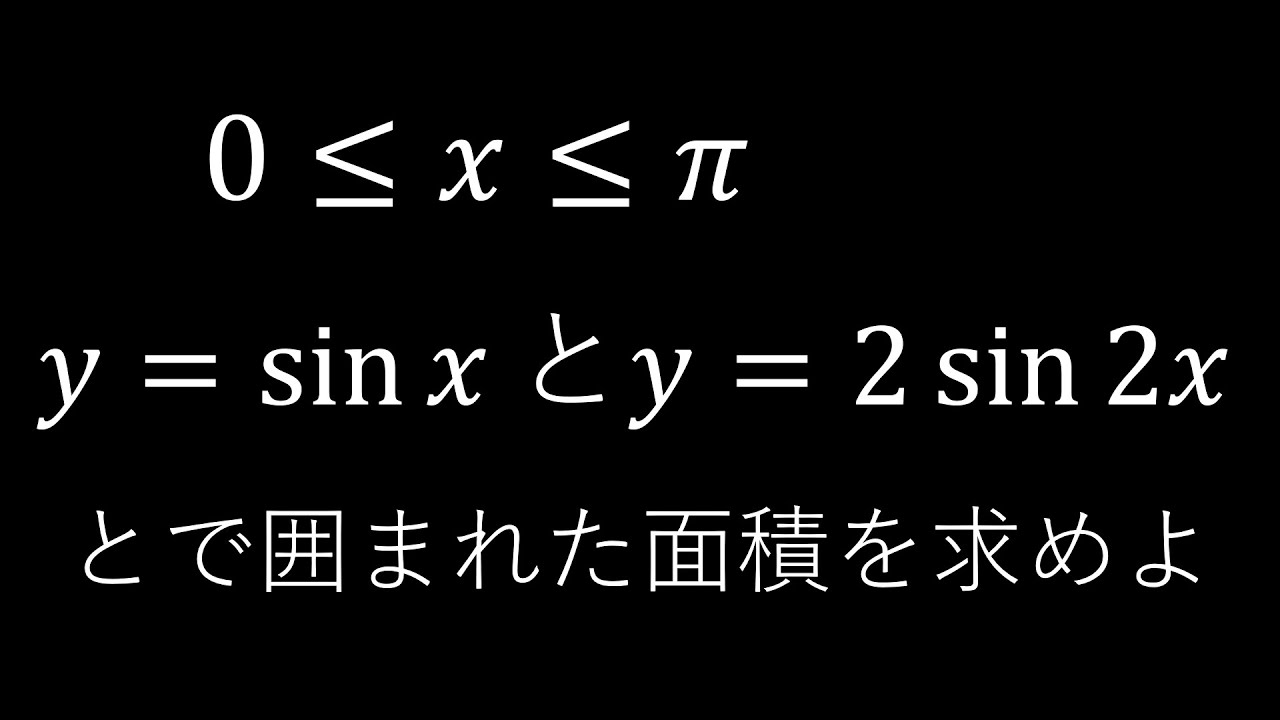問題文全文(内容文):
$(1)f(x)=3x^2-2x+ \displaystyle \int_{-1}^{1}f(t)dtを満たす関数f(x)を求めよ.$
$(2)f(x)=3x+\displaystyle \int_{0}^{1}(x+t)f(t)dtを満たす関数f(x)を求めよ.$
$(3)y=\displaystyle \int_{1}^{x}(t^2-2t-3)dtの極値を求めよ.$
$(4)\displaystyle \int_{1}^{x}f(t)dt=3x^2-2x+aを満たす関数f(x)と定数aを求めよ.$
$(1)f(x)=3x^2-2x+ \displaystyle \int_{-1}^{1}f(t)dtを満たす関数f(x)を求めよ.$
$(2)f(x)=3x+\displaystyle \int_{0}^{1}(x+t)f(t)dtを満たす関数f(x)を求めよ.$
$(3)y=\displaystyle \int_{1}^{x}(t^2-2t-3)dtの極値を求めよ.$
$(4)\displaystyle \int_{1}^{x}f(t)dt=3x^2-2x+aを満たす関数f(x)と定数aを求めよ.$
単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$(1)f(x)=3x^2-2x+ \displaystyle \int_{-1}^{1}f(t)dtを満たす関数f(x)を求めよ.$
$(2)f(x)=3x+\displaystyle \int_{0}^{1}(x+t)f(t)dtを満たす関数f(x)を求めよ.$
$(3)y=\displaystyle \int_{1}^{x}(t^2-2t-3)dtの極値を求めよ.$
$(4)\displaystyle \int_{1}^{x}f(t)dt=3x^2-2x+aを満たす関数f(x)と定数aを求めよ.$
$(1)f(x)=3x^2-2x+ \displaystyle \int_{-1}^{1}f(t)dtを満たす関数f(x)を求めよ.$
$(2)f(x)=3x+\displaystyle \int_{0}^{1}(x+t)f(t)dtを満たす関数f(x)を求めよ.$
$(3)y=\displaystyle \int_{1}^{x}(t^2-2t-3)dtの極値を求めよ.$
$(4)\displaystyle \int_{1}^{x}f(t)dt=3x^2-2x+aを満たす関数f(x)と定数aを求めよ.$
投稿日:2022.09.25